离散数学运算-概念与例子

在介绍代数系统之前，先引进一个集合A上的运算概念。例如，将实数集合R上的每一个数a≠0映射成它的倒数1/a，或者将R上的每一个数y映射成[y]，就可以将这些映射称为在集合R上的一元运算；而在集合R上，对任意两个数所进行的普通加法和乘法，都是集合R上的二元运算，也可以看作是将R上的每两个数映射成R中的一个数。上述这些例子，有一个共同的特征，那就是其运算结果都是在原来的集合R中，我们称具有这种特征的运算是封闭的，简称闭运算。相反地，没有这种特征的运算就不是封闭的。

很容易举出不封闭运算的例子：一架自动售货机，能接受一角硬币和二角伍分硬币，而所对应的商品是橘子水（瓶）、可口可乐（瓶）和冰激凌（杯）。当人们投入上述硬币的任何两枚时，自动售货机将按表1所示的供应相应的商品。

表1

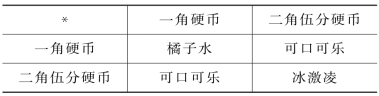
表格左上角的记号*可以理解为一个二元运算的运算符。这个例子中的二元运算*就是集合{一角硬币，二角伍分硬币}上的不封闭运算。

定义1 对于集合A，一个从An到A的映射，称为集合A上的一个n元运算。n称为运算的阶。当n=2时，称为A上的二元运算。下面着重讨论二元运算的一些性质。

定义2 设*是定义在集合A上的二元运算，如果对于任意的x，y∈A，都有x*y∈A，则称二元运算*在A上是封闭的。

例1 设A={x|x=2n，n∈N}，问乘法运算是否封闭？对加法运算呢？

解 对于任意的2r，2s∈A，r，s∈N，因为2r·2s=2r+s∈A，所以乘法运算是封闭的。而对于加法运算不是封闭的，因为至少有2+22=6∉A。

定义3 设*是定义在集合A上的二元运算，如果对于任意的x，y，z∈A都有（x*y）*z=x*（y*z），则称该二元运算*是可结合的。

例2 设A是一个非空集合，☆是一个A上的二元运算，对于任何a，b∈A，a☆b=b，证明☆是可结合运算。

证明 因为对于任意的a，b，c∈A

(a☆b)☆c=b☆c=c

而

a☆(b☆c)=a☆c=c

所以

(a☆b)☆c=a☆(b☆c)

定义4 设*是定义在集合A上的二元运算，如果对于任意的x，y∈A，都有x*y=y*x，则称该二元运算*是可交换的。

例3 设Q是有理数集合，Δ是Q上的二元运算，对任意的a，b∈Q，aΔb=a+b-a·b，问运算Δ是否可交换？

解 因为

aΔb=a+b-a·b=b+a-b·a=bΔa

所以运算Δ是可交换的。

定义5 设*，Δ是定义在集合A上的两个二元运算，如果对于任意的x，y，z∈A，都有

x*(yΔz)=(x*y)Δ(x*z)

(yΔz)*x=(y*x)Δ(z*x)

则称运算*对运算Δ是可分配的。

例4 设集合A={α，β}，在A上定义两个二元运算*和Δ，如表2所示，运算Δ对于运算*可分配吗？运算*对于运算Δ呢？

表2

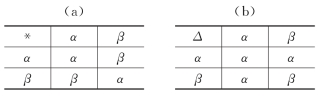
解 容易验证运算Δ对于运算*是可分配的。但是运算*对运算Δ是不可分配的，因为

β*(αΔβ)=β*α=β

而

(β*α)Δ(β*β)=βΔα=α

定义6 设*，Δ是定义在集合A上的两个可交换二元运算，如果对任意的x，y∈A，都有(www.xing528.com)

x*(xΔy)=x

xΔ(x*y)=x

则称运算*和运算Δ满足吸收律。

例5 设集合N为自然数全体，在N上定义两个二元运算*和☆，对于任意x，y∈N，有

x*y=max{x,y}

x☆y=min{x,y}

验证运算*和☆的吸收律。

解 对于任意a，b∈N，

a*(a☆b)=max{a,min{a,b}}=a

a☆(a*b)=min{a,max{a,b}}=a

因此，*和☆满足吸收律。

定义7 设*是定义在集合A上的一个二元运算，如果对于任意的x∈A，都有x*x=x，则称运算*是等幂的。

例6 设P（S）是集合S的幂集，在P（S）上定义的两个二元运算，集合的“并”运算∪和集合的“交”运算∩，验证∩，∪是等幂的。

解 对于任意的A∈P（S），有A∪A=A和A∩A=A，因此运算∪和∩都满足等幂律。

定义8 设*是定义在集合A上的一个二元运算，如果有一个元素el∈A，对于任意的元素x∈A，都有el*x=x，则称el为A中关于运算*的左幺元；如果有一个元素er∈A，对于任意的元素x∈A都有x*er=x，则称er为A中关于运算*的右幺元；如果A中的一个元素e，它既是左幺元又是右幺元，则称e为A中关于运算*的幺元。显然，对于任一x∈A，有e*x=x*e=x。

例7 设集合S={α，β，γ，δ}，在S上定义的两个二元运算*和☆，如表3所示。试指出左幺元或右幺元。

解 由表3可知β、δ都是S中关于运算*的左幺元，而α是S中关于运算☆的右幺元。

表3

定理1 设*是定义在集合A上的一个二元运算，且在A中有关于运算*的左幺元el和右幺元er，则el=er=e，且A中的幺元是唯一的。

证明 因为el和er分别是A中关于运算*的左幺元和右幺元，所以

el=el*er=er=e

设另有一个幺元e1∈A，则

e1=e1*e=e

定义9 设*是定义在集合A上的一个二元运算，如果有一个元素θl∈A对任意的元素x∈A都有θl*x=θl，则称θl为A中关于运算*的左零元；如果有一个元素θr∈A，对于任意的元素x∈A，都有x*θr=θr，则称θr为A中关于运算*的右零元；如果A中的一个元素θ，它既是左零元又是右零元，则称θ为A中关于运算*的零元。显然，对于任一x∈A，有

θ*x=x*θ=θ

例8 设集合S={浅色，深色}，定义在S上的一个二元运算*如表4所示。

表4

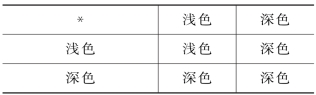
试指出零元和幺元。

解 深色是S中关于运算*的零元，浅色是S中关于运算*的幺元。

定理2 设*是定义在集合A上的一个二元运算，且在A中有关于运算*的左零元θl和θr，那么θl=θr=θ，且A中的零元是唯一的。

这个定理的证明与定理1相仿。