有向图矩阵表示及可达性

定义7 设G=＜P，L＞是一个简单有向图，它有n个顶点，P={v1，v2，…，vn}，则n阶方阵A=（aij）称为G的邻接矩阵。其中

注意：与无向图不同，有向图的邻接矩阵不一定是对称的。

例5 如图5所示

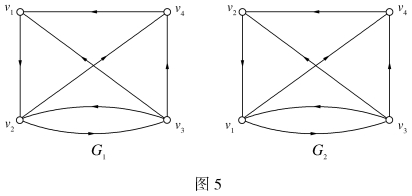
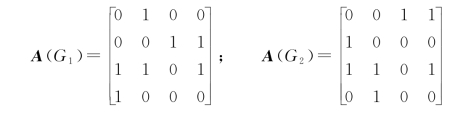
由上例可见，邻接矩阵与顶点的标定次序有关，如在图4（G1）中，若将v1和v2的次序调换一下，那么新的矩阵A（G2）是原矩阵A（G1）的第一、二行对调，第一、二列对调而得到的。

一般地说，我们把一个n阶方阵A的某些行作一置换，再把相应的列作同样的置换，得到一个新的矩阵A1，我们称A1与A是置换等价的。有向图的顶点，按不同的次序所写出的邻接矩阵是彼此置换等价的，今后我们略去这种元素次序的任意性，可取图的任意一个邻接矩阵作为该图的邻接矩阵。

从邻接矩阵A中，我们看到，第i行元素是由结点vi出发的边决定，第i行中值为1的元素数目等于vi的出度。同理，在第j列中值为1的元素数目是vj的入度。

如果给定一个图是零图，则其对应的矩阵中，所有元素都为零即它是一个零矩阵，反之亦然。

从图G的邻接矩阵中，我们还可以得到图的很多重要性质：

设有向图G的顶点集P={v1，v2，…，vn}，它的邻接矩阵为：A（G）=（aij）n×n，现在我们想计算从顶点vi到顶点vj的长度为2的路的数目。注意到每条从vi到vj的长度为2的路，中间必须经过一个结点vk，即vi→vk→vj（1≤k≤n），如果图G中有路vivkvj存在，那么aik=1且akj=1，即aik·akj=1。于是从顶点vi到顶点vj的长度为2的路的数目等于：

按着矩阵的乘法规则，这恰好等于矩阵A2中第i行、第j列的元素。

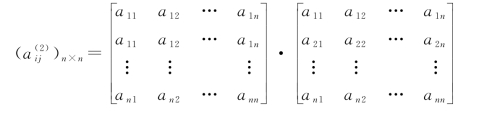
表示从vi到vj的长度为2的路的数目。

表示从vi到vi的长度为2的回路数目。

从vi到vj的长度为3的路，可以看作是由vi到vk的一条长度为1的路，再联结vk到vj的一条长度为2的路，故vi到vj的长度为3的路的数目：

即。

一般地有：

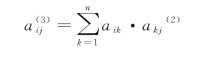
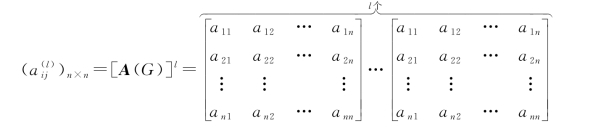
上述这个结论对无向图也成立。

定理4 设A（G）是图G的邻接矩阵，则[A（G）]l中的第i行、第j列元素等于G中联结vi与vj的长度为l的路的数目。

证明 对l用数学归纳法。

当l=2时，由上可知显然成立。

设命题对l成立，由

[A(G)]l+1=A(G)·(A(G))l

故

根据邻接矩阵的定义，aik表示联结vi与vk的长度为1的路的数目，是联结vk与vj的长度为l的路的数目，故上式右边的每一项表示由vi经过一条边到vk，再由vk经过一条长度为l的路到vj的总长度为l+1的路的数目。对所有k求和，即得是所有从vi到vj的长度为l+1的路的数目，故命题对l+1成立。

例6 给定一图G=＜P，L＞，如图6所示。

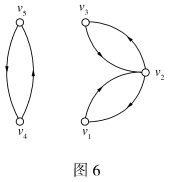
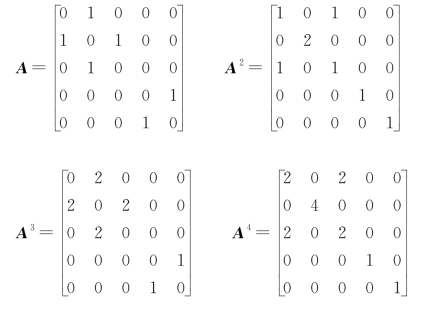
从上述矩阵中我们可以想到一些结论，如v1与v2之间有两条长度为3的路，结点v1与v3之间有一条长度为2的路，在结点v2有四条长度为4的回路，但没有长度为3的回路。

在许多实际问题中，常常要判断有向图的一个顶点vi到另一个顶点vj是否存在路的问题。如果利用图G的邻接矩阵A，则可计算A，A2，…，An，…，当发现其中某个Al的，就表明结点vi到vj可达，但这种方法比较烦琐且Al不知计算到何时为止。为解决这一问题，我们给出如下定理。

定理5 在一个具有n个顶点的图中，若从顶点vi到顶点vj存在一条路，则必存在一条从vi到vj的长度小于n的路。证略。

由定理5，对于有向图G，若G有n个顶点，P={v1，v2，…，vn}，vi到vj有一条路，则必然有一条长度不超过n的路，因此只要考察就可以了，其中1≤l≤n。对于有向图G中任意两个顶点之间的可达性，亦可用矩阵表达。(www.xing528.com)

定义8 设G=＜P，L＞是一个简单有向图，|V|=n，假定G的顶点已编序，即P={v1，v2，…，vn}，定义一个n×n阶矩阵P={bij}。

其中 称矩阵P是图G的可达性矩阵。

可达性矩阵表明了图中任意两个顶点之间是否存在一条路以及在任何顶点上是否存在回路。

一般地讲，可由图G的邻接矩阵A得到可达性矩阵P，即令Bn=A+A2+…+An，再从Bn中将非零元素改为1，为零的元素不变，改换以后所得到的矩阵即为可达性矩阵P。

例7 设G如图7所示，利用邻接矩阵A求G的可达性矩阵P。

解 由图7，邻接矩阵

可达性矩阵

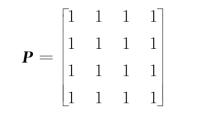
由此可知图G中任两顶点间均是可达的，并且任一顶点均有回路，因而此图是一个强连通图。

上述计算可达性矩阵的方法还是比较复杂，因为可达性矩阵是一个元素为0或1的布尔矩阵，由于在Al中，我们所关心的是两顶点间是否有路存在，而对于有几条路不感兴趣，因此我们可将矩阵A，A2，…，An分别改为布尔矩阵A（1），A（2），…，A（n），故可达性矩阵P=A（1）∨A（2）∨…A（n），其中A（i）表示在布尔运算意义上A的i次方，“∨”为布尔和。

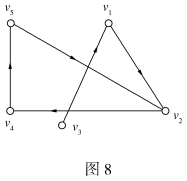
例8 设图G如图8所示，求可达性矩阵P。

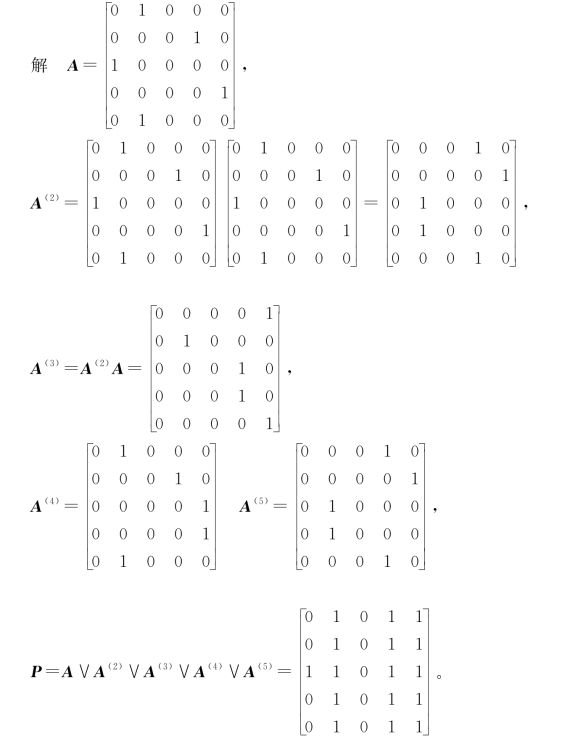
上述可达性矩阵等概念，可以很容易地推广到无向图中，只要将无向图中每条无向边看成是具有相反方向的两条边，这样，一个无向图就可以看成是有向图。无向图的邻接矩阵是一个对称矩阵，其可达性矩阵称为连通性矩阵，它也是对称的。

对于无向图，我们定义了关联矩阵，对于有向图，我们可类似地定义关联矩阵。

定义9 给定简单有向图G=＜P，L＞，其中P={v1，v2，…，vn}，L={l1，l2，…，lq}，称n×q阶矩阵M（G）=（mij）为G的关联矩阵，其中

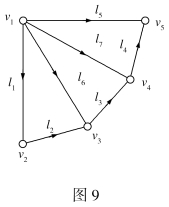
例9 如图9所示，关联矩阵

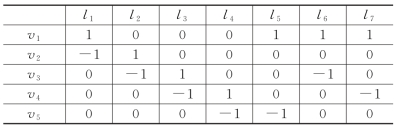
即

从有向图的关联矩阵中可以得到图G的一些性质：

（1）图中每一边关联两个顶点，故M（G）的每一列只有两个非零元素。

（2）每一行中非零元素的个数为其对应顶点的度，1的个数为该结点的出度，-1的个数为该顶点的入度。

（3）一行中元素全为0，其对应顶点为孤立点。

（4）同一图当顶点或边的编序不同时，其对应的M（G）仅有行序、列序的差别。

若记vi对应的行为i，按着普通的加法，将vi与vj的对应元素相加并记为vi⊕vj=vij，对矩阵M（G）施以上述运算，实际上就是将图中的vi与vj点合并。

设图G的顶点vi与vj合并后得到图G′，则M（G′）是将M（G）中vi与vj相加得到。因为若有关项中第r个对应分量有mir⊕mjr=±1，则说明vi和vj两者之中只有一个是lr的端点，且将两顶点合并后的顶点Vij仍是lr的端点。

若mir⊕mjr=0，则有两种情况：

1）vi与vj都不是lr的端点，那么vij也不是lr的端点。

2）vi和vj都是lr的端点，那么合并后在G′中lr成了vij到自身的一条边，我们规定将该边删去。

此外，在M（G）中，若有某些列，其元素全为零，说明G中的一些顶点在合并后，消失了一些对应边。

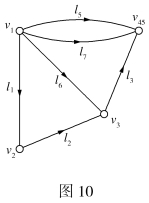
例如，在图9中合并顶点v4和v5而得到v45，如图10所示，在矩阵中，就是将第4行与第5行相加得M（G′），如下：