离散数学：有向图的连通性

定义4 设G=＜P（G），L（G）＞是一个有向图，若在G中存在一条从顶点u到顶点v的有向路，则称从u可达v。

可达性是有向图结点集P（G）上的二元关系，它是自反的和传递的，但一般来讲，它不是对称的。因为如果从u到v有一条有向路，不一定必有从v到u的一条有向路，故可达性不是等价关系。

如果u可达v，它们之间可能不止一条路，在所有这些路中，最短的长度称为点u和v之间的距离（或最短线），记作d＜u，v＞，它满足下列性质：

d＜u,v＞≥0;

d＜u,u＞=0;

d＜u,v＞+d＜v,w＞≥d＜u,w＞。

其中u，v，w都是G的顶点。如果从u到v是不可达的，则通常写成d＜u，v＞=∞。

注意：当u可达v且可达u时，d＜u，v＞不一定等于d＜v，u＞。我们把称作图G的直径。

定义5 给定有向图G=＜P（G），L（G）＞，如果G中任意两个顶点都是相互可达的，则称G是强连通的。如果对于G中的任两个顶点u和v，或者从u可达v，或者从v可达u，则称G是单侧连通的。如果在图中略去边的方向，将它看成无向图时是连通的，则称G是弱连通的。

例3 如图3所示

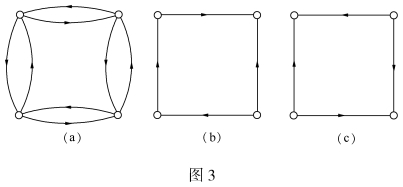
（a）是强连通图，（b）是单侧连通图，（c）是弱连通图。

从上述定义可以看出，若G是强连通图，则它必是单侧连通图；若G是单侧连通图，则它必是弱连通图。这两个命题，其逆不真。

定理2 一个有向图G是强连通的，当且仅当G中有一条回路，它至少包含每个顶点一次。(www.xing528.com)

证明 充分性

如果G中有一个回路，它至少包含每个顶点一次，则G中任两个顶点都是相互可达的，故G是强连通的。

必要性

如果有向图G是强连通的，则任两个顶点都是相互可达的，故必可作一回路经过图中所有各点。若不然则必有一回路不包含某一顶点v，并且v与回路上的各顶点不是相互可达，与强连通条件矛盾。

定义6 在简单有向图中，具有强连通性质的最大子图，称为强分图；具有单侧连通性质的最大子图，称为单侧分图；具有弱连通性质的最大子图，称为弱分图。

例4 如图4所示

在图4（a）中，由{v1，v2，v3，v4}或{v5}导出的子图都是强分图，由{v1，v2，v3，v4，v5}导出的子图是单侧分图，也是弱分图。

又如在图4（b）中，强分图可由{v1}，{v2}，{v3}，{v4}导出，单侧分图可由{v1，v2，v3}，{v1，v3，v4}导出，弱分图可由{v1，v2，v3，v4}导出。

定理3 在有向图G=＜P，L＞中，它的每一个顶点位于且只位于一个强分图中。

证明（1）假设v∈P，令S是G中所有与v相互可达的顶点的集合，当然v也在S中，而S的导出子图是G的一个强分图，因此G的每个顶点都必位于一个强分图中。

（2）假设v位于G的两个不同的强分图G1=＜P1，L1＞和G2=＜P2，L2＞之中，因为G1中每个顶点与v相互可达，而v与G2中的每个顶点也相互可达，故G1中任一顶点与G2中任一顶点通过v都互相可达，这与题设G1为强分图矛盾。故G的每一结点只能位于一个强分图中。