欧拉公式：可平面图的顶点、边和面之间的关系

下面我们介绍能表明一个可平面图顶点、边和面之间的关系的著名的欧拉（Euler）公式。

定理2 设G是连通的平面图，顶点数是v，边数是ε，面数是φ，则有

v-ε+φ=2

证明 对G的面数φ使用数学归纳法，如果φ=1，则G无回路，又因G连通，因此G是树。由树的性质知具有v个顶点的树有v-1条边，在这种情形下，v-ε+φ=v-（v-1）+1=2，定理显然成立。

假设定理对任何少于n个面的图都是正确的。

现在设G是具有n（n≥2）个面的连通图。因为G有两个以上的面，所以G有回路C，在回路C中选一边e，在G中删去e后得图G′，则G′仍是一个连通的平面图，G′有n-1个面。根据归纳假设知

v(G′)-ε(G′)+φ(G′)=2

但因v（G′）=v（G），在G中删去一边后把两个面合为一个面，所以有

ε(G′)=ε(G)-1, φ(G′)=φ(G)-1

因此

v(G)-ε(G)+φ(G)=2

推论1 设G是连通简单平面图，G的顶点数v≥3，则G的边数ε≤3v-6。

证明 设G是连通简单图，顶点数≥3，则对G的任意面f，都有dG（f）≥3，因此有

其中φ是图G的面数。

根据定理1知，

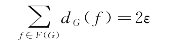
因此有2ε≥3φ，即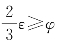

根据Euler公式得出

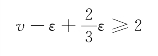
由此推出ε≤3v-6。

推论2 设G是连通简单可平面图，则G中各点的最小度δ≤5。

证明 当顶点数v＜4，推论显然成立，根据第四章第一节定理1知，图中各点度的总和是边数的2倍，因此有

(www.xing528.com)

由此推出δ≤5。

例2 证明K5不是平面图。

证明 用反证法，假设K5是平面图，按推论1，K5的边数应小于或等于3v-6=3×5-6=9，但K5有10条边，矛盾。

例3 证明图6所示的图K3.3不是平面图。

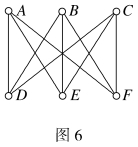
证明 用反证法，若K3.3可以改画成平面图G，则因K3.3没有长度小于4的回路，G的每个面的度数必大于或等于4，设G的面数为φ，则有

因此φ≤4，于是

v-ε+φ≤6-9+4=1

而由Euler公式知v-ε+φ=2，推出矛盾。

K5和K3.3是两种十分重要的非可平面图。Kuratowski于1930年证明了任何一个非可平面图都有同胚于K5或K3.3的子图。

定义3 设G1是一个图，如果G2是以一条链（端点度为1，中间诸点皆为2的简单路）代替G1的一边所得图，则称G1和G2具有同胚的边。如果G1和G2具有n个同胚边（n≥0），则称G1和G2是同胚的。

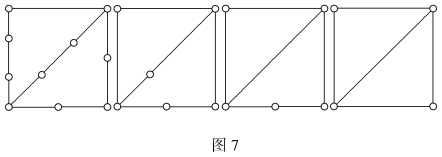
例如，图7中4个图是同胚的。

显然，若G1和G2是同胚的，则或者它们都是可平面图，或者它们都是非可平面图。

因为K5和K3.3是非可平面的，如果一个图有同胚于K5或K3.3的子图，这个图一定是非可平面图。1930年Kuratowski证明了这个条件也是非可平面图的必要条件，即是说，若一个图是非可平面图，则必有同胚于K5与K3.3的子图。因此可以总结成下面的定理。

定理3（Kuratowski，1930）一个图是可平面图，当且仅当它不含同胚于K5与K3.3的子图。

因为定理3的证明是十分复杂的，涉及图论的很多其他知识，我们略去了它的证明。下面举出了定理3的一个应用例。

例4 证明图8所示的图G不是可平面图。

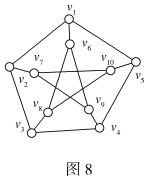
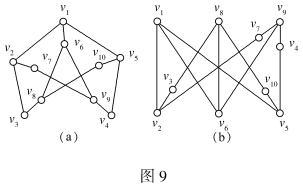
证明 因为图G1有子图G2，如图9（a）所示，可以改画成图9（b）的形式，由此知G2同胚于K3.3。因为G1有同胚于K3.3的子图，所以是非可平面图。