本节我们介绍平面图,平面图的研究在许多实际问题中,例如集成电路的布线设计中,有着广泛的应用。
定义1 设G=<P,L>是图,如果能把G画在一个平面内,使得图的各边除在端点外彼此都不相交,则G称为可平面图。
如果已经画在平面内,并且图中各边互不相交,则G称作平面图。
例如,图1中的(a)是可平面图,因为我们可以把它改画成平面图,如图1中(b)的形状。
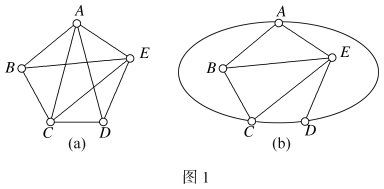
但是,有些图无论怎样改画,都不可避免地会有相交的边,这样的图才是非可平面图。
为举出一个非平面图的例子,我们先介绍平面Jordan曲线的性质。
起点与终点重合,自身又互不相交的平面曲线叫Jordan曲线。在平面图的研究中,Jordan曲线起着非常重要的作用,因为图中的回路构成了一条Jordan曲线。
设J是平面中一条Jordan曲线,如图2所示,则平面被J分成两个不相交的区域,分别叫作J的内部和J的外部,用int(J)和ext(J)表示。Jordan曲线的一个重要性质是:若点u∈int(J),点v∈ext(J),则连接点u和v的任意曲线必然和J相交。
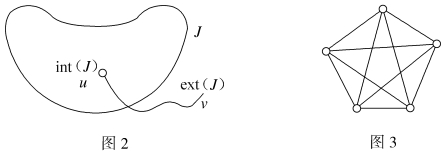
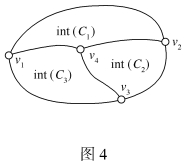
例1 证明图3所示的由5个顶点构成的完全图K5不是可平面图。
假设可以把K5改画成一个平面图G,用v1,v2,v3,v4和v5表示G的顶点,因为G是完全图,它的任意两个顶点之间都有边相连。回路C=v1v2v3v1构成一个Jordan曲线,如图4,顶点v4或者在int(C)中或者在ext(C)中,不妨假定v4∈int(C),(当v4∈ext(C)时可以用类似的方式处理),于是边v4v1,v4v2,v4v3把int(C)分成3个区域int(C1),int(C2),int(C3),其中C1=v1v4v2v1,C2=v2v4v3v2,C3=v3v4v1v3,v5必须位于ext(C),int(C1),int(C2),int(C3)四个区域的某一区域中,如果v5∈ext(C),则因为v4∈int(C),根据Jordan曲线的性质,v4v5的连线必然与C相交,这与G是可平面图矛盾。类似地,可以证明当v5∈int(Ci)(i=1,2,3)时也会导致矛盾。
定义2 设G是平面图,则G把平面划分成一些连通的区域,这些区域称为G的面。
例如图5所示的平面图把平面分成4个面:f1,f2,f3和f4。今后,我们用F(G)表示G的面集合,Φ(G)表示G的面数。每一个平面图都恰有一个无限的面,称为外部面,图5中f1是外部面。
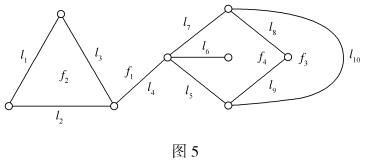
设G是图,不在G的任何回路上的边称为割边,例如图中l4和l6是割边,设f是G的面,与f相邻的边的总数(割边要计算两次)称为面f的度,记作dG(f)。例如在图5中,dG(f1)=8,dG(f2)=3,dG(f3)=3,dG(f4)=6。(https://www.xing528.com)
定理1 设G是可平面图,G有ε条边,则
![]()
换句话说,平面图各面的度数总和是边数的二倍。
证明 对G的边数使用数学归纳法。
若G只有一条边,则G只有一个面f1,且dG(f1)=2,定理显然成立。
假设定理对边数小于n的任何可平面图都是正确的。
设G是具有n条边的可平面图,以下分两种情况讨论。
(1)G中有点v的度是1,设v在G的面f1中,则删去与v相连的边e,得图G′,G′有n-1条边,由归纳假设知
![]()
现在在G′中添上边e,重新得到G,则因为e在G中是割边,dG(f)=dG′(f1)+2,而对任何i≠1,dG(fi)=dG′(fi),所以有
![]()
(2)G中点的度都不是1,则G有一回路C,设C由l条边组成,C包围的面是fC。在回路C中删去一边e,得图G′,由归纳假设知
![]()
现在在G′中添上e,重新得到G,则G比G′增加了一个度为l的面fc,而另外一个面的度减少了l-2,因此总度数之和增加2。所以仍有
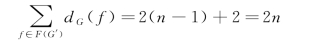
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




