与欧拉回路非常类似的问题是汉密尔顿回路的问题。1859年，威廉·汉密尔顿爵士（Sir Willian Hamilton）在给朋友的一封信中，首先谈到关于十二面体的一个数学游戏：能不能在图3中找到一条回路，使它含有这个图的所有结点？他把每个结点看成一个城市，连接两个结点的边看成是交通线，于是他的问题就是能不能找到旅行路线，沿着交通线经过每个城市恰好一次，再回到原来的出发地？他把这个问题称为周游世界问题。
按图3所给的编号，可以看出这样一条回路是存在的。
对于任何连通图也有类似的问题。
定义2 给定图G，若存在一条路经过图中的每个结点恰好一次，这条路称作汉密尔顿路。若存在一条回路，经过图中的每个结点恰好一次，这条回路称作汉密尔顿回路。具有汉密尔顿回路的图称为汉密尔顿图。
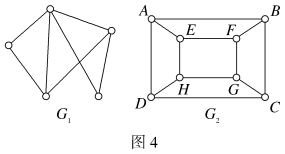
例1 下面的图4为汉密尔顿图。
在图G2中，路（ABCDHGFE）是汉密尔顿路，路（ABCDHGFEA）是汉密尔顿回路。
欧拉路与汉密尔顿路的研究目的不同，前者要遍历图的所有边，后者要遍历图的所有点。虽然都是遍历问题，两者的困难程度却大不相同。对于欧拉路，在前面我们已经得到一些较为深刻的定理，比较满意地解决了这一问题。但对于后者，却没有令人满意的结果，许多研究者仍就这一问题在进行深入的研究。
对于汉密尔顿路与汉密尔顿回路，下面的一些性质是显然的。
（1）汉密尔顿路是简单路。设G有n个顶点，则G的汉密尔顿路有n-1条边，G的汉密尔顿回路有n条边。
（2）若G中某点度为0，则G既无汉密尔顿路，也无汉密尔顿回路。若G中某点的度为1，则G无汉密尔顿回路。
（3）设v是G中的一个顶点，d（v）=2，若G有汉密尔顿回路，则以v为端点的两条边必须都出现在汉密尔顿回路中。
（4）汉密尔顿回路要求遍历诸点，如果图中某些必须在汉密尔顿回路中出现的边已经构成回路，而图中尚有不在该回路中出现的点，则该图一定没有汉密尔顿回路。
（5）设v是图G的一个点，d（v）＞2，G有汉密尔顿回路，则汉密尔顿回路仅使用以v为端点的两条边。
例2 如图5所示。若G3有汉密尔顿回路，则因A，B，C，D四点的度都是2，以此四点为端点的边必须都出现在汉密尔顿回路中，因为以此四点为端点的边已经构成回路，但E，F两点不在回路中，所以G3没有汉密尔顿回路。
例3 图6所示G4有汉密尔顿路，没有汉密尔顿回路。
设G4有汉密尔顿回路L，则边AC，AB必在L中，同理，边DF，DC，EG，EC也必在L中。于是，在回路L中，通过点C有三条边AC，DC，EC，这不可能，因此G4无汉密尔顿回路。
G4的汉密尔顿路是（ACDFBGE）。
例4 图7所示G5设有汉密尔顿回路仅使用以L为端点的两边，抛弃其余的3边，对点H和J也有类似的情况，因此有从L，H，J三点出发的9条边不在汉密尔顿回路中。
点F的度是3，汉密尔顿回路仅使用以F为端点的两条边，以F为端点的一条边不在回路中，同样的情形出现在点B，O，D，因此有4条分别以F，B，O，D为端点的边不在汉密尔顿回路中。
综上所述，可知G5有13条边不在它的汉密尔顿回路中。G5共有27条边，因此，G5的汉密尔顿回路中最多包含27-13=14条边。但是另一方面，G5有16个点，G5的汉密尔顿回路应该有16条边，推出矛盾，因此G5无汉密尔顿回路。
作为汉密尔顿图的一个应用，就是货郎担问题，一个货郎要到若干个村庄去推销货物，最后又回到出发点，他面临着怎样选择一条路程最短的路线问题。这个问题用图论的术语来描述：构造图G=＜P，L＞，图中各点相应于货郎要去的所有村庄，图中各边相应于连接两个村庄之间的道路。设每边（vivj）的权Lij＞0，它等于边（vivj）旅行的距离（或时间，或费用）。包含图中每个点一次且仅一次的一条回路，就是汉密尔顿回路，而具有最小权和汉密尔顿回路，就是货郎担问题。
定理2 如果图G=＜P，L＞是汉密尔顿图，则对于P（G）的任一非空子集S，都有
W(G-S)≤|S|(www.xing528.com)
其中|S|表示S中点的个数，W（G-S）表示图G-S的分枝数。
证明 设C是G中的汉密尔顿回路。显然
W(C-S)≤|S|
（在回路中，依次删去S中的点以及与此点邻接的两条边，每次最多只增加一个分枝，且删去第一个点时，不增加分枝）。
又因C是G的支撑子图，所以C-S是G-S的支撑子图，因此W（G-S）≤W（C-S），所以
W(G-S)≤|S|
证毕。
定理2经常被用来证明一个图不是汉密尔顿图。如果能在图G中找出一点集S，使得在G中删去S后所得图的分枝数大于S中顶点的个数，则G不是汉密尔顿图。
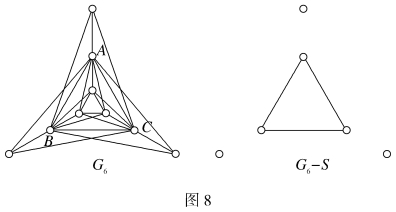
例5 如图8所示，把G6中点A，B，C构成的集合记为S，则从图G6中删去S，得图G6-S，图G6-S的分枝数W（G-S）=4，而|S|=3，由定理2知图G6不是汉密尔顿图。
下面的定理给出了一个图是汉密尔顿图的充分条件。
定理3 若G=＜P，L＞是有限图，
，则G是汉密尔顿图。其中|P（G）|表示图G中顶点个数，δ（G）是G的最小度。
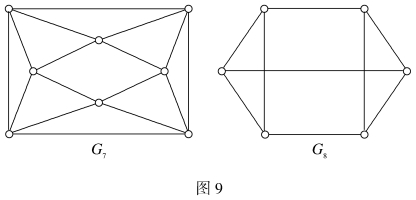
例6 如图9所示，如果记r=|P（G）|，则在G7中，r=8，δ=4，在G8中，r=6，δ=3。
定理4 设G是有限图，u和v是G中不邻接的两点，并且满足d（u）+d（v）≥r，则G是汉密尔顿图的充要条件是G∪{uv}是汉密尔顿图。其中r=|P（G）|，G∪{uv}表示在G中加入边uv。
定义3 设G是有限图，反复连接G中不邻接的并且其度之和不小于r的点对，直到没有这样的点对为止，最后所得之图称为G的闭合图（或闭包），记作C（G）。
例7 如图10所示G9，其闭合图C（G9）形成过程如下。
定理5 有限图的闭合图是唯一确定的。
定理6 有限图G是汉密尔顿图的充要条件是其闭合图C（G）是汉密尔顿图。
利用定理6可以证明图9中的G7和G8是汉密尔顿图。
推论 设G是有限图，若C（G）是完全图，则G是汉密尔顿图。
用此推论可以导出很多用点的度来表示关于图是汉密尔顿图的充分条件。例如，当
时，对图中任意两点u和v，都有
d(u)+d(v)≥r
故该图的闭合图是完全图，因此该图是汉密尔顿图。由此可见，定理3的条件实际上是上述推论的一个特例。
汉密尔顿图的判定是图论中一个较为困难的问题，这里我们只介绍了一些初步的结果，感兴趣的读者可以进一步阅读有关材料。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
