欧拉(Euler)是18世纪瑞士数学家,图论的创始人。1736年,他在一篇开创性的论文中,讨论了一个有趣的问题,即所谓哥尼斯堡(Knoigsberg)城七桥问题。这个城市就是现在的加里宁格勒,位于普列格河(Pregel)两岸并包括河中的两个岛屿,于是城市被分成了四部分。各部分通过七座桥互相连接,如图1(a)所示。每逢假日,城中居民进行环城游玩,这样就产生了一个问题:“能否从某地出发,经过每座桥一次且恰好一次再回到出发地。”
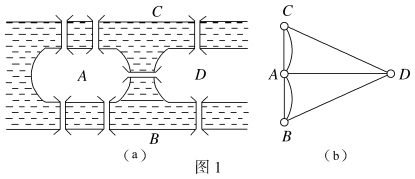
因为这里的兴趣在于过桥,所以可以把A,B,C,D想象成点,而把桥想象成线,于是得到图1(b)所示的图形。现在的问题是,是否能够从图1(b)所示的图形中的某一点出发,遍历各条边恰好一次,又回到原来的出发点?欧拉经过认真研究后指出,这是不可能的。欧拉路和欧拉图也因此而得名。
定义1 给定无孤立顶点的图G,若存在一条路,经过图中每条边一次且仅一次,则称该路为一条欧拉路。若存在一条回路经过图中每条边一次且仅一次,则该回路称为欧拉回路。具有欧拉回路的图称作欧拉图。
定理1 无向图G具有一条欧拉路,当且仅当G是连通的,且有零个或两个奇数度顶点。
证明 必要性
设G具有欧拉路,即有点边序列v0e1v1e2v2…eiviei+1…ekvk,其中结点可能重复出现,但边不重复,因为欧拉路经过所有图G的结点,故图G必是连通的。
对任何一个不是端点的结点vi,在欧拉路中每当vi出现一次,必关联两条边,故vi虽可重复出现,但d(vi)必是偶数。对于端点,若v0=vk,则d(v0)为偶数,即G中无奇数度结点,若端点v0与vk不同,则d(v0)为奇数,d(vk)为奇数,G中有两个奇数度结点。
充分性
若图G连通,有零个或两个奇数度结点,我们构造一条欧拉路如下:
(1)若有两个奇数度结点,则从其中的一个结点开始构造一条迹,即从v0出发经关联边e1“进入”v1,若d(v1)为偶数,则必可由v1再经关联边e2进入v2,如此进行下去,每边仅取一次。由于G是连通的,故必可到达另一奇数度结点停下,得到一条迹L:v0e1v1e2v2e3…viei+1…vk。若G中没有奇数度结点,则从任一结点v0出发,用上述方法必可回到结点v0,得到上述一条闭迹L1。(https://www.xing528.com)
(2)若L1通过G的所有边,则L1就是欧拉路。
(3)若G中去掉L1后得到子图G′,则G′中每个结点度数为偶数,因为原来的图是连通的,故L1与G′至少有一个结点vi重合,在G′中由vi出发重复(1)的方法,得到闭迹L2。
(4)当L1与L2组合在一起,如果恰是G,则得欧拉路,否则重复(3)可得到闭迹L3,依此类推直到得到一条经过图G中所有边的欧拉路。
推论 无向图G具有一条欧拉回路,当且仅当G是连通的,并且所有结点度数全为偶数。
由于有了欧拉路和欧拉回路的判别准则,因此哥尼斯堡七桥问题立即有了确切的否定答案。因为从图1(b)中可以看到dG(A)=5,dG(B)=dG(C)=dG(D)=3,故欧拉回路必定不存在。
欧拉路问题是一个实用性很强的问题。如果把一个邮递员所要投递信件的街道看成是图的边,它当然希望能够毫无遗漏而又不重复地走遍所有的边,通常把这一问题称为邮递线路问题。在智力游戏中,有时需要我们判定一个图形是否可以一笔画出来,即在画图的过程中要求不重复且笔尖一直不离开纸面,这个问题通常称作一笔画问题。邮递路线问题和一笔画问题实际上都是欧拉路是否存在的问题。
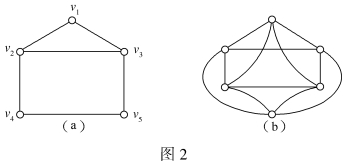
要判定一个图G是否可一笔画出,有两种情况:一是从图G中某一结点出发,经过图G的每一边一次且仅一次到达另一结点。再一种就是从G的某个结点出发,经过G的每一边一次且仅一次再回到该结点。上述两种情况分别可以由欧拉路和欧拉回路的判定条件予以解决。如图2(a)中,因为d(v2)=d(v3)=3,d(v1)=d(v4)=d(v5)=2,故必有从v2到v3的一笔画。在图2(b)中所有结点度数均为偶数,所以可以从任一点出发,一笔画回到原出发点。
欧拉路和欧拉回路的概念,很易推广到有向图中去。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




