离散数学：加权图的最短路问题解决方案

定义7 设G=＜P，L＞是有限图，如果对L（G）中的每一条边l，都有一个实数w（l）附着其上，则称G为权图，称w（l）为边l的权，规定对任意u∈P，w（u，u）=0，当两点u和v不邻接时，w（u，v）=∞。

例如，设G是一个描述各城市间的铁路交通图，对于图G的每一条边，我们可以把连接两城市间的铁路长度附着其上，作为这条边所具有的权，这样这个铁路交通图就变成权图。我们还可以把两城市间的铁路修建费用附着其上作为权，这样的铁路交通图也是一个权图。

可以想象，在一个权图中，任给两点u和v，从u到v可能有几条路，在这些路中，求出所带权的总和最小的那条路是有实际意义的。在表示铁路长度的权图中，所带权总和为最小的路意味着从u旅行到v的费用最低。在表示建筑费用的权图中，所带权总和最小的路意味着从u修建铁路到v的造价最低。这个问题也称作是求权图中的最短路问题，这条最短路所带权的总和称为从u到v的距离，记作d（u，v）。

1959年，迪克斯特拉（Dijkstra）给出了一个在权图中求任意两点间最短路的算法，我们把这个算法简略叙述如下。

设G=＜P，L＞是一个有限权图，l是G中一条路，我们把l上所带权的总和叫作l的权和，记作|l|。又设S是G中某些点做成的集合，u0是S中一个点，，我们把从u0出发到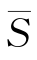中点的具有最小权和的路叫作从u0到的距离，记作。迪克斯特拉算法通过递归地计算，求出u0在所有其余点的最短路。

设P（G）=（u0，u1，…，un），

（1）令，(www.xing528.com)

重复执行上述过程，直到求出了u0到un的距离d（u0，un）即最短路ln为止。

例4 在图5中，我们用迪克斯特拉算法依次求出了u0到其余7个点的最短路，其最短路在图上用黑色粗线标出。

迪克斯特拉算法的主要思想是利用点到点集的最短路代替两点间的最短路，这种替换有助于形成递归过程，而且可以统筹考虑，一次求出u0到所有其余点的最短路。当然，这种替换的可靠性是需要证明的，因篇幅所限，我们略去了这一证明。