离散数学（上册）：图的连通性及其度量

定义4 设G=＜P，L＞是图，u和v是G中两点，如果存在一条从u到v的路，则称u与v是连通的。若一个图中的任何两点均连通，则称该图为连通图。

顶点的连通是顶点集P上的等价关系，因此按着这个等价关系，必可将P分成非空等价类P1，P2，…，Pm，使得顶点vj和vk连通当且仅当vj和vk同属一个Pi，我们称子图G（p1），G（p2），…，G（pm）是G的连通分支（图）。

显然只有一个连通分支的图即是连通图。

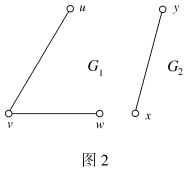
例3 如图2所示，结点u和w是连通的，而u和x不是连通的。G1和G2是G的连通分支。

对于连通图，常常由于删除了图中的顶点或边而影响了图的连通性。所谓在图中删除顶点v，即是把v以及与v关联的边都删去。例如：在图3（a）中删去v3，即由（a）变为（b）。图中删除某边，仅需把该边删去，如在图3（a）中删除边l变为图（c）。

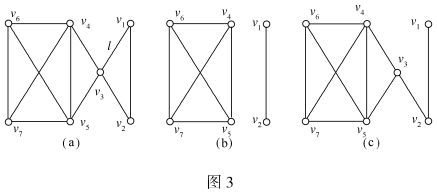
定义5 设G=＜P，L＞为连通图，若点集P1⊂P，使图G中删除P1中的所有顶点后，所得的子图是不连通图或平凡图，而删除P1的任何真子集后，得到的图仍是非平凡的连通图，则称P1是G的一个点割集。由一个顶点构成的点割集称为割点。如图3（a），P1={v4，v5}，P2={v3}均为点割集，P2={v3}是割点。

如记K（G）=min{|P1||P1是G的点割集}，则称K（G）为图G的点连通度（或连通度）。连通度就是为了产生一个不连通图或平凡图需要删去的点的最少数目。显然K（Kn）=n-1，不连通的图或平凡图的连通度为0。

定义6 设图G=＜P，L＞为连通图，若有边集L1⊂L，使图G删除L1中所有边后得到的子图不连通，而删除L1的任何真子集后仍连通，则称L1是G的一个边割集。只含一条边的割集称为割边或桥。

令

λ（G）=min{|L1||L1是G的边割集}

称λ（G）为G的边连通度。

边连通度就是为了产生一个不连通图需要删除边的最少数目。规定不连通图或平凡图的λ（G）=0。

惠特尼定理 对任何G=＜P，L＞，有

K(G)≤λ(G)≤δ(G)(www.xing528.com)

证明 若G为不连通图或平凡图，则K（G）=λ（G）=0，上式成立。

若G为非平凡的连通图，

（1）证明λ（G）≤δ（G）

设v∈P，且d（v）=δ（G），则与v关联的所有边组成的集合L1是G的一个边割集，由λ（G）的定义知λ（G）≤|L1|=δ（G）。

（2）证明K（G）≤λ（G）

1）设λ（G）=1，这时G有一条桥e=uv，且u，v中至少有一点为G的割点，故K（G）=1，K（G）≤λ（G）。

2）设λ（G）≥2，则必可删除λ（G）条边使G不连通，而删去其中λ-1条边，它仍连通，且有一条桥e=uv。对λ-1条边中的每条边都选取一个异于u，v的端点。把这些端点删去则必至少删去λ-1条边，若这样产生的图不连通，则K（G）＜λ（G）。若这样产生的图是连通的，则e仍为桥，此时再删去u或v，则必产生一个不连通图，故K（G）≤λ（G）。

由（1）和（2）得

K(G)≤λ(G)≤δ(G)

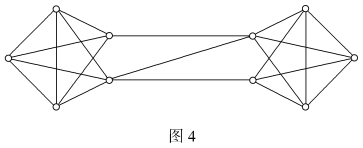
如图4所示，这里K（G）=2，λ（G）=3，δ（G）=4。

定理 一个连通图中的顶点v是割点的充分必要条件是存在两点u和w，使任何uw路都通过顶点v。

证明 若v是G=＜P，L＞的割点，则G-v不连通，设G1=＜P1，L1＞，G2=＜P2，L2＞是G-v的两个分支，任取u∈P1，w∈P2，则G中任何uw路必通过v。

反之，设G中存在两点u和w，使任何uw路都经过点v，则G-v中不存在uw路，故G-v必不连通，所以v是割点。