集合基数概念及验证两个集合等势

为了比较两个集合的“大小”，确定有限集和无限集的概念，这里首先需要引进自然数集合。

定义1 给定集合A的后继集定义为集合：

A+=A∪{A}

若A为空集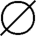，则后继集为+，（+）+，（（+）+）+，…这些集合可写成如下形式：

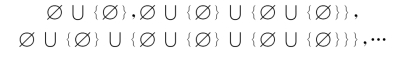
可简化为：

若我们命名集合为0，那么，

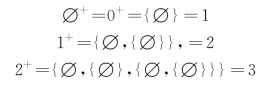
这样就得到了自然数集合{0，1，2，3，…}，这个集合亦能概括为如下公理形式（G.Peano公理）。

（1）0∈N（其中0=）。

（2）如果n∈N，那么n+∈N（其中n+=n∪{n}）。

（3）如果一个子集S⊆N具有性质：

(a)0∈S。

（b）如果n∈S，有n+∈S，则S=N。

性质（3）称极小性质，它指明了自然数系统的最小性，即自然数系统是满足公理（1）和（2）的最小集合。

当然，自然数集，亦可不从0开始，这只需定义为1，则自然数集就从1开始。

从上述定义可以看到任意一个自然数可看作是一个集合的名。此外，从实际生活中我们知道任意自然数，例如3这个概念是从观察许多只含三个元素的集合的共同特点而加以抽象概括出来的，这个共同特点就是体现于这些被观察的任意一个集合的元素都可与集合{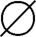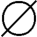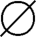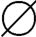，{}，{，{}}}中的元素存在一一对应，且其任意两个集合的元素之间也存在一一对应。由此可见，“对应”是集合之间进行比较的一个非常重要的概念。

定义2 给定两个集合P与Q，如果我们对P中每个不同元素，与Q中每个不同元素，可以分别两两成对，那么我们就说P的元素与Q的元素间存在着一一对应。

例如，{2，4，6，8…，2n，…}与{1，3，5，…，2n-1，…}之间存在着一一对应。

定义3 当且仅当集合A的元素与集合B的元素之间存在着一一对应，集合A与集合B称为是等势的（或称同浓的），记作A～B。

例1 验证自然数集N与非负偶数集合M是等势的。

证明 因为N与M的元素之间可作一一对应的映射，即

f(n)=2n

例2 设P为实数集合，S是P的子集，即S⊆P，且

S={x|x∈P∧0＜x＜1}(www.xing528.com)

证明：S～P。

证明 令f：P→S，

显然f的值域是S，且f是双射。

定理1 在集合族上等势关系是一个等价关系。

证明 设集合族为S，

（1）对任意A∈S，必有A～A。

（2）若A，B∈S，如果A～B，必有B～A。

（3）若A，B，C∈S，如果A～B且B～C，必有A～C。

定义4 如果有一个从集合{0，1，…，n-1}到A的双射函数，那么称集合A是有限的；如果集合A不是有限的，则它是无限的。

定理2 自然数集合N是无限的。

证明 设n是N的任意元素，f是任意的从{0，1，…，n-1}到N的函数。设k=1+max{f（0），f（1），…，f（n-1）}，那么k∈N，但对每一个x∈{0，1，…，n-1}，有f（x）≠k。因此f不能是入射，即f也不是双射。因为n和f都是任意的，故N是无限的。

对于有限集的大小概念很容易理解，对于无限集的度量要考虑到集合的等势关系。

设有集合A，一切与该集合等势的集合，其元素之间可以一一对应，若以此作为度量标准，我们可有如下定义。

定义5 所有与集合A等势的集合所组成的集合，叫作集合A的基数，记为K[A]（或A）。

从基数的定义可以看到，有限集合的基数就是其元素的个数。

例如，A={a，b，c}，B={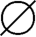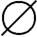，{}，{，{}}}，C={桌，灯泡，教室}，…，因为A～B～C，即K[A]=K[B]=K[C]。

K[A]={A,B,C,…}

可以看到，如果两个集合能够建立双射，则两集合元素间必一一对应，从基数的定义可以知道，该两集合应具有相同的基数。

例3 证明区间[0，1]与（0，1）基数相同。

证明 设集合

定义f：[0，1]→（0，1）使得：

则f是双射，如图1所示。