离散数学-第八节序关系，关系图和半序关系

由关系矩阵和关系图都可看出，R具有自反性、反对称性，且易证R具有传递性，故R是半序关系。

例2 证明在实数集R上，小于等于关系“≤”是半序关系。

证明（1）对任意x∈R，有x≤x，故“≤”是自反的；

（2）对任意x，y∈R，若x≤y且y≤x，则x=y，所以“≤”是反对称的；

（3）对任意x，y，z∈R，若x≤y且y≤z，则x≤z，故“≤”是传递的。

因此，“≤”是半序关系。证毕。

例3 给定集合A={a，b，c，d}，令R={（a，b），（a，a），（b，b），（c，c），（d，d），（c，d）}，证明R是半序关系。

证明 写出R的关系矩阵和画出关系图（图2）：

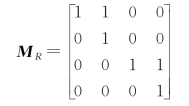
由关系矩阵可看出主对角线元素均为1，所以R是自反的，由关系图看出任意两结点没有成对出现的有向弧，所以R是反对称的，又因（a，b）∈R，且（b，b）∈R则（a，b）∈R，…，逐个验证可知R是传递的，所以R是A上的半序关系。证毕。

对于给定的半序集，可以通过简化了的关系图来表示，这种图称为半序集合图或称哈斯（Hasse）图。它的作图规则如下：

（1）由于关系“≤”是自反的，所以在原关系图中每个结点上都有自回路，为了作图方便，省略每个结点上的自回路，只用了一个空心点表示集合中的元素。

（2）由于关系“≤”是反对称的，原关系图中如果结点a与结点b（a≠b）之间有弧，一定是单向的，我们规定，如果a≤b，就把b画在a的上方，也就是把原关系中结点的位置作适当调整，使得所有弧的方向都是向上的，这样可以略去弧上的箭头。

（3）由于关系“≤”是传递的，若a≤b，b≤c，a≤c，即从a到b有一条弧，从b到c也有一条弧，我们规定，省略掉从a到c的一条弧。也就是说，若某两结点之间有一连串带箭头的头尾相接的弧连接，那么就省略掉这两结点间的一条弧。

例4 设集合A上具有整除关系|，试对（1）A={1，2，3，6，10，12，16}，（2）A={4，7，14，21，28，32}分别画出半序集（A，|）的哈斯图。

解 先写出整除关系：

(1)|={(2,6),(2,10),(2,12),(2,16),(2,2),(3,3),(3,6),(3,12),(6,6),(6,12),(10,10),(12,12),(16,16),(1,1),(1,2),(1,3),(1,6),(1,10),(1,12),(1,16)};

(2)|={(4,4),(4,28),(4,32),(7,7),(7,14),(7,21),(7,28),(14,14),(14,28),(21,21),(28,28),(32,32)}。

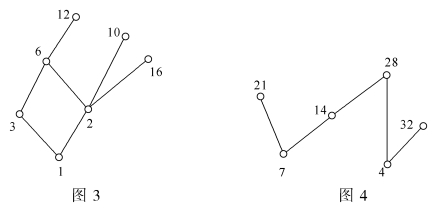
哈斯图分别如图3和图4所示。

例5 绘出例1和例3中的半序关系R的哈斯图。

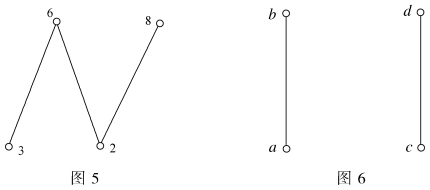
解 例1和例3中的半序关系哈斯图分别如图5和图6所示。

例6 设集合A={a，b，c}，（ρ（A），⊆）是半序集合，试画出它的哈斯图。

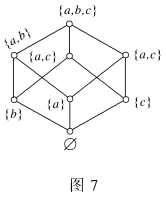
解 因为A={a，b，c}，所以ρ（A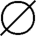）={，{a}，{b}，{c}，{a，b}，{b，c}，{a，c}，{a，b，c}}，由此可画出哈斯图如图7所示。从哈斯图中可看到，半序集A中各个元素处于不同层次的位置。下面我们讨论半序集中具有一些特殊位置的元素。

定义2 设（A，≤）是一个半序集，B是A的任一子集，若B中有一元素b，对所有的x∈B，都有x≤b，则称b为集合B的最大元；若有某个元素b∈B，对所有的x∈B，都有b≤x，则称b为集合B的最小元。

在例4（1）中，数1是集合A的最小元，集合A不存在最大元，因为10不能整除16；但若取B={1，2，3，6，12}，则B的最小元是1，最大元是12。在例4（2）中，集合A既没有最小元，也没有最大元，因为28不能整除32，4不能整除7。若取B={4，7，14，28}，则B的最大元是28，没有最小元。

例1、例2中的集合A既无最大元也无最小元。

例6中ρ（A）的最大元是{a，b，c}，最小元是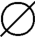，而在B={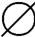，{a}，{b}，{c}，{a，c}}中，最大元不存在，最小元仍是。

定义3 设（A，≤）是一个半序集，B是A的任一子集，若对于B中的某个元素b，在B中没有任何元素x，能同时满足b≠x与b≤x，则称b为B的极大元；若B中没有任何元素x，能同时满足b≠x与x≤b，则称b为B的极小元。

在例4（1）中，A的极大元是10，12，16，极小元是1，而若取B={1，3，16}，则B的极大元是3，16，极小元仍是1。在例4（2）中，A的极大元是21，28，32，极小元是4，7。

例6中，幂集ρ（A）的极大元也是最大元，是{a，b，c}，极小元也是最小元，是。

关于最大元、最小元、极大元和极小元，有下面的定理；(www.xing528.com)

定理1 设（A，≤）是半序集，B是A的任一子集，若B有最小元（最大元），则是唯一的。

证明 设a和b是B的最小元，则有a≤b和b≤a。因为半序关系≤是反对称的，所以有a=b，因此最小元是唯一的。

同理可证最大元的情况。证毕。

定理2 设（A，≤）是半序集。B是A的任意子集，则B的最大元必为极大元，B的最小元必为极小元。

证明 设b是集合B的最大元，即对于所有的x∈B，都有x≤b，这样在B中找不到任何元素y，能同时满足y≠b且b≤y，因此b是B的极大元。同理可证，B的最小元是B的极小元。证毕。

由于最大（最小）元是唯一的，而极大（极小）元不一定是唯一的，所以定理2的逆定理不成立。

例7 设A={2，3，5，7，14，15，21}，其半序关系R={（2，14），（3，15），（3，21），（5，15），（7，14），（7，21），（2，2），（3，3），（5，5），（7，7），（14，14），（15，15），（21，21）}。求B={2，7，3，21，14}的极大元与极小元。

解 R的关系图如图8所示。

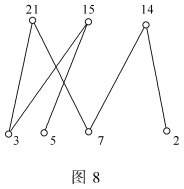
由关系图可知，B的极小元素集合为{2，3，7}，极大元素集合为{21，14}。

定义4 设（A，≤）是一个半序集，B是A的任意非空子集，元素a∈A。

（1）若对于x∈B，都有x≤a，则称a为B的上界；若对于任意x∈B，都有a≤x，则称a为B的下界。

（2）若a是B的上界，且对于B的任意上界b，都有a≤b，则称a是B的最小上界；若a是B的下界，且对于B的任意下界b，都有b≤a，则称a是B的最大下界。

应当注意，一般地，上界与最大元（或极大元）的区别在于元素a所取的集合不同，对于B⊆A，B的上界a∈A，而最大元（或极大元）的a∈B。

例8 设集合A={a，b，c，d，e}上的半序关系如图9的哈斯图所示。

（1）试求出集合A的最大元、最小元、极大元和极小元。

（2）分别求出子集B1={a，b，c}，B2={b，c，d}，B3={c，d，e}的上界、下界、最小上界和最大下界。

解（1）A无最大元，最小元c，极大元集合{b，d}，极小元集合{c}。

（2）B1的上界是b，下界是c，最大下界是c，最小上界是b。B2无上界，下界是c，最大下界是c，无最小上界。

B3的上界是d，下界是c，最大下界是c，最小上界是d。

例9 半序集合（A，R）的哈斯图如图10所示。

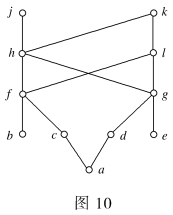
（1）求A的最大元、最小元、极大元、极小元、上界、下界、最大下界和最小上界。

（2）设B1={f，g，h，l}，B2={a，b，c，d，e，f，g，h，}，分别求出最大元、最小元、极大元、极小元、上界、下界、最大下界、最小上界。

解（1）A无最大元和最小元，极大元为{j，k}，极小元为{a，b，e}，无上界和下界，也无最小上界和最大下界。

（2）B1无最大元和最小元，极大元为{h，l}，极小元为{f，g}，上界为k，下界为a，最小上界是k，最大下界是a。

B2的最大元是h，没有最小元，极大元是h，极小元是{a，b，e}，上界是{h，j，k}，无下界，最小上界是h，无最大下界。

定义5 在半序集（A，≤）中，如果A是一个链，则称（A，≤）为全序集合或称线序集合，在这种情况下，二元关系“≤”称为全序关系或称线关系。

链A就是对任意x，y∈A，或者有x≤y或者有y≤x成立。

例如，定义在自然数集合N上的“小于等于”关系“≤”是半序关系，且对任意i，j∈N，必有：（i≤j）或（j≤i）成立，故也是全序关系。

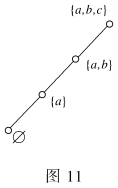
例10 给定P={，{a}，{a，b}，{a，b，c}}上的包含关系⊆，证明（P，⊆）是个全序集合。

证明 因为⊆{a}⊆{a，b}⊆{a，b，c}，故P中任意两元素都有包含关系，如图11所示。