反自反关系R2的特性及传递关系的证明

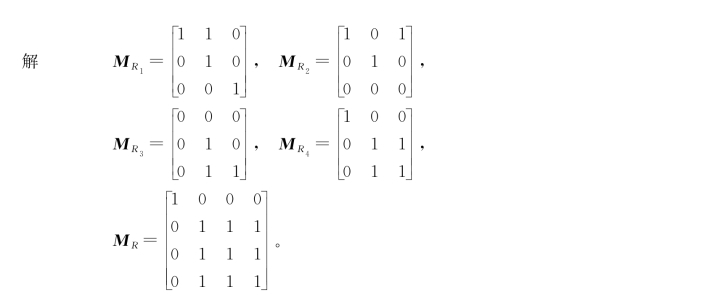
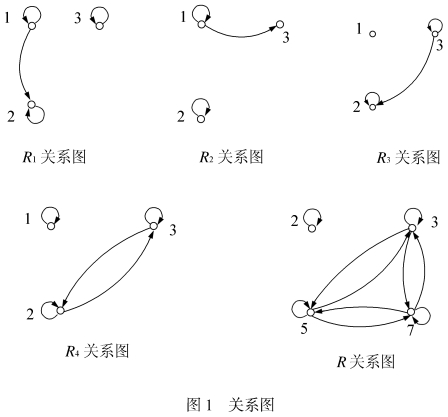
在反自反关系R2的关系矩阵中，主对角线元素全为零，关系图中无自回路。

定义5 集合A上的二元关系R满足对任意x，y∈A，若（x，y）∈R且（y，x）∈R，必有x=y，则称R在A上是反对称的（或R是A上的反对称关系）。

换句话说，集合A上的二元关系R满足对任意x，y∈A，若（x，y）∈R，则当x≠y时，（y，x）∉R，则称R在A上是反对称的。

例如，实数集合R上的小于或等于关系“≤”是反对称的关系。又如，集合中的包含关系“⊆”也是反对称的。

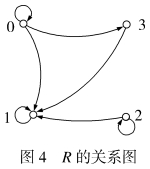
例11 设集合A={0，1，2，3}，R是A上的关系：R={（0，0），（0，1），（0，3），（1，1），（2，1），（2，2），（3，1）}，试判断R在A上具有反对称性。

解 根据反对称关系的定义，在集合R中，如果有序偶（a，b）∈R，或者a=b，或者（b，a）∉R，而题目所给出的关系R恰好满足上述情况，所以R是A上的反对称关系。

其关系矩阵的特点是，若aij=1（i≠j），则有aji=0，而主对角线上的元素是1或者0。其关系矩阵为

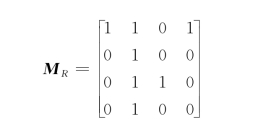
R的关系图如图4所示，关系图的特点是，如果两个结点间有弧，则只有一条；结点有自回路或者没有自回路。

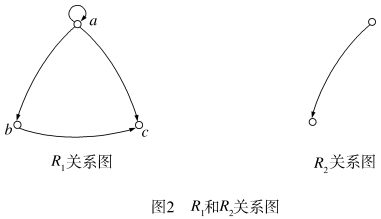
例12 设A={a，b，c，d}上的关系R1={（a，a），（b，b）}，R2={（a，b），（b，c），（c，b）}，R3={（a，d），（d，c）}，R4={（a，b），（b，c），（c，d）}。讨论R1，R2，R3，R4的对称性、反对称性。

解 R1既是对称的，也是反对称的；(www.xing528.com)

R2既不是对称的，也不是反对称的；

R3是反对称的；

R4是反对称的。

一般地，用关系矩阵与关系图来判断一种关系R是否是自反的、对称的、反对称的和传递的，有如下规律：

（1）若关系R具有自反性，当且仅当在关系矩阵中，主对角线上元素全为1。或者在关系图中每个结点都有一条自回路。

（2）若关系R具有对称性，当且仅当关系矩阵是对称矩阵。或者在关系图中，若两个结点间存在有向弧，必是成对的。

（3）若关系R具有传递性，关系矩阵没有明显特征。关系图的特点是：任意两个结点ab间若通过一条以上的弧能连接起来的话，则必有一条从a到b的弧。

（4）若关系R具有反自反性，当且仅当关系矩阵主对角线元素为零，或者关系图无自回路。

（5）若关系R具有反对称性，当且仅当关系矩阵中以主对角线对称的元素不能同时为1（可以同时为0），而主对角线上的元素是1或者是0。或者在关系图上两个结点间的有向弧不可能成对出现，结点可以有自回路。

例13 设R1和R2是集合A上的自反关系，试证明R-11，R1∩R2，R1∪R2也是集合A上的自反关系。

证明 对于集合A中的任意元素a，若R1为A上的自反关系，有（a，a）∈R1，则（a，a）∈R-11，故R-11是A上的自反关系。

对于任意a∈A，由R1和R2是A上的自反关系，有（a，a）∈R1，且（a，a）∈R2，则（a，a）∈R1∩R2，故R1∩R2是A上的自反关系。

同理可证，R1∪R2也是A上的自反关系。证毕。

例14 设关系R1和R2是集合A上的对称关系，试证明R-11，R1∩R2，R1∪R2也是A上的对称关系。

证明 对任意（a，b）∈R-11，则（b，a）∈R1，因为R1是对称的，（a，b）∈R1，于是（b，a）∈R-11，即证R-11是A上的对称关系。证毕。

同理可证，R1∩R2，R1∪R2也是A上的对称关系。

例15 设关系R1和R2是集合A上的传递关系，试证明，R-11，R1∩R2也是A上的传递关系。

证明（1）对任意x，y，z∈A，若（x，y）∈R-11，且（y，z）∈R-11，则有（y，x）∈R1且（z，y）∈R1，由R1的传递性知（z，x）∈R1，所以有（x，z）∈R-11，故R-11是传递的。

（2）对任意x，y，z∈A，若（x，y）∈R1∩R2，且（y，z）∈R1∩R2，则（x，y）∈R1，（x，y）∈R2，（y，z）∈R1，（y，z）∈R1。由于R1、R2是传递的，所以有（x，z）∈R1且（x，z）∈R2，因此（x，z）∈R1∩R2，故R1∩R2也是A上的传递关系。证毕。