计数制基本概念：基数、进位、位权和运算规则

1.数制

数制就是用一组固定的数字和一组统一的规则表示数的方法。

数制的种类很多，“12个月等于1年”是十二进制；“1小时等于60分，1分钟等于60秒”是六十进制；“7天为一周”是七进制，人们日常生活中最熟悉的是十进制。在计算机中主要涉及四种进制：十进制、二进制、八进制、十六进制。

任何一种数制都可以用以下四个规则来描述：基数规则、进位规则、位权规则、运算规则。每一种计数制都使用一组特定的数字符号，把这些符号按序排列，由低到高进位，用以表示一个数的计数方法称为“计数制”；该计数制中允许选用的基本数码的个数称为“基数”；每个数码所表示的数值等于该数码乘以一个与数码所在位置相关的常数，这个常数称为“位权”，位权的大小是以基数为底、数码所在位置的序号为指数的整数次幂。

二进制：基数为2，数字包括0、1；“逢二进一”，位权为2的幂。

八进制：基数为8，数字包括0、1、2、3、4、5、6、7；“逢八进一”，位权是8的幂。

十进制：基数为10，数字包括0、1、2、3、4、5、6、7、8、9；“逢十进一”，位权是10的幂。

十六进制：基数为16，数字包括0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。其中A～F表示10～15；“逢十六进一”，位权是16的幂。

由于存在多种不同的进制，因此在给出一个数时，应指明它的数制。为了区别不同数制表示的数，通常在数的后面注明数制，或在末尾加上表示进制的英文字母，十进制数用D表示，二进制数用B表示，八进制数用O表示，十六进制数用H表示。

如：（1010）2或1010B（Binary）表示二进制数，（1010）8或1010O表示为八进制数，（1010）10或1010D表示为十进制数，（1010）16或1010H表示为十六进制数。数制的规则即其进位原则，N进制就是逢N进1。几种制到数的对应关系如表1-2所示。(www.xing528.com)

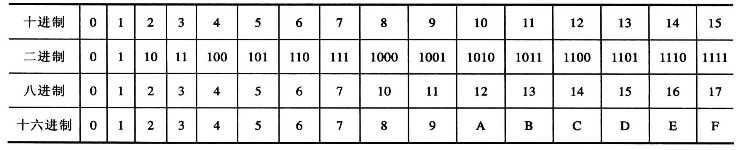
表1-2　几种进制数的对应关系

2.二进制数的特点

（1）可行性。采用二进制，只有0和1两个状态，需要表示“0”、“1”两种状态的电子器件很多，如开关的接通和断开，晶体管的导通和截止、磁元件的正负剩磁、电位电平的低与高等都可表示0、1两个数码。使用二进制，电子器件具有实现的可行性。

（2）简易性。二进制数的运算法则少，运算简单，使计算机运算器的硬件结构大大简化。十进制的乘法九九口诀表有55条公式，而二进制乘法只有4条规则见表1-3。

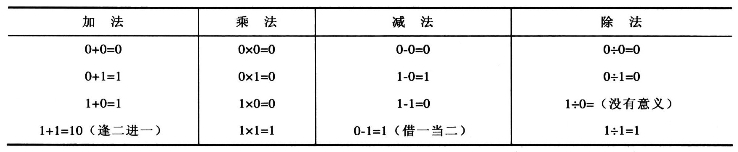
表1-3　二进制数的运算规则

（3）能方便使用逻辑代数。二进制数的“0”和“1”与逻辑代数“假”（false）和“真”（true）相对应，可使算术运算和逻辑运算共用一个运算器，易于进行逻辑运算。

（4）记忆和传输可靠。有两种稳定状态的电子元件，若用“0”和“1”表示两种状态，其工作可靠、抗干扰强、存储和可靠性好，不易出错。