使用函数单调性与极值证明的方法解决不等式

例8.18 设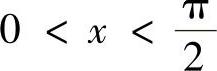，证明：

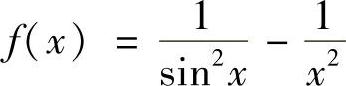证明 令，则

于是

令

则

由此知g′（x）在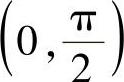上单调递增，故g′（x）>g′（0）=0.于是知g（x）在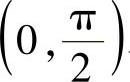上单调递增，故g（x）>g（0）=0，从而f′（x）>0，这样就有

即

推论 当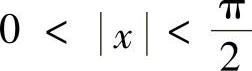时，证明：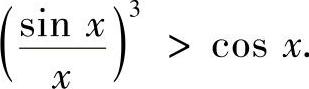

例8.19 设0<x<1，证明：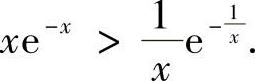

证明 原不等式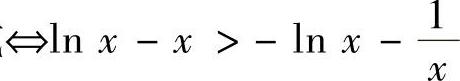

令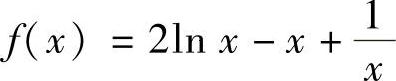，则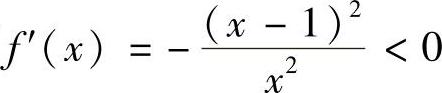，故f（x）在（0，1）上单调递减.于是f（x）>f（1）=0，从而原不等式成立.

例8.20 设x，y>0，β>α>0，证明：

证明 不妨设y≥x，将原不等式变形为：

取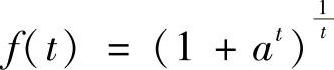，a≥1，t>0，则

由此知，

由此知，g（t）在（0，+∞）上单调递减，所以g（t）<g（0）=-2ln2<0，故f′（t）<0.于是f（t）在（0，+∞）上单调递减，从而原不等式成立.

类题 设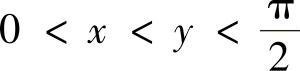，证明下列不等式：

例8.21 设b>a>0，证明

（河南大学）.

证明 将原不等式改写为：

先证左边的不等式.

令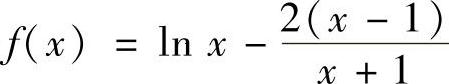，则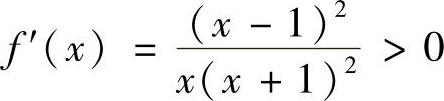，所以f（x）在x>1上单调递增，于是有f（x）>f（1）=0，即

再证右边的不等式.

为此令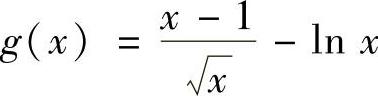，则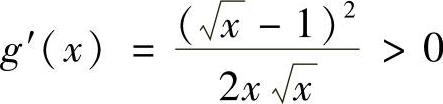，x>1，所以g（x）在x>1上单调递增，于是有g（x）>g（1）=0，即

类题　设m>n>0，证明：

例8.22　证明不等式

（中科院—中科大）.

证明　原不等式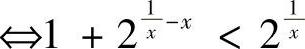，x∈（0，1）.令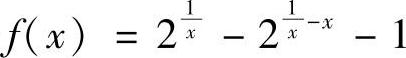，则f（1）=0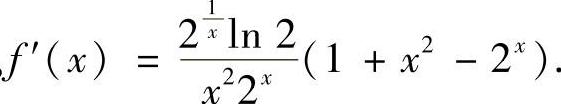，而 f′（x）<0⇔1+x²-2^x<0，

⇔ln（1+x²）-xln2<0，　x∈（0，1）.

令g（x）=xln2-ln（1+x²），则g（0）=g（1）=0，

由此知，g（x）在（0，1）上是凹函数，故g（x）>0，x∈（0，1）.从而f′（x）<0，即f（x）在（0，1）上严格单减.于是f（x）>f（1）=0，这样就证明了原不等式.

例8.23　证明当a>b>1时，成立不等式

证明　原不等式等价于

若记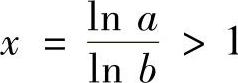，y=lnb>0，则上式可进一步化为：lnx>y（xe^y-e^xy）. （1）

引入辅助函数f（y）=xe^y-e^xy，则f′（y）=x（e^y-e^xy）<0，所以

f（y）<f（0）=x-1.

若f（y）≤0，由lnx>0，y>0可知，lnx>0>yf（y），即式（1）成立；

若f（y）>0，即xe^y-e^xy=e^y（x-e^（x-1）y）>0，由此可知，

e^lnx-e^（x-1）y>0，

亦即 lnx>（x-1）y.

注意到f（y）<x-1，∀y>0，由上式可得

lnx>（x-1）y>yf（y），

即式（1）也成立.从而只要a>b>1，原不等式总成立.

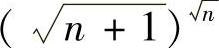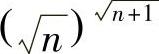类题1　设a，b>0，a≠b，问在什么条件下成立a^b>b^a？并由此比较eπ与πe及与的大小？

提示　将原不等式取对数化成：

令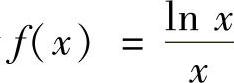，考察f（x）在（0，+∞）的单调性.

类题2　设0<x<y，证明不等式：

（中科院—中科大）.

提示　令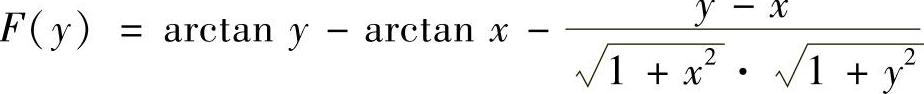，则(www.xing528.com)

注意到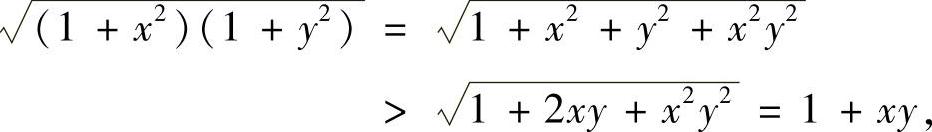可知，F′（y）>0.

例8.24　设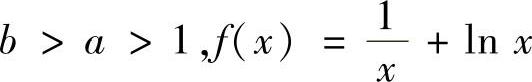，证明：

证明　由拉格朗日中值定理知，∃ξ∈（a，b），使得

因为上式右端大于0，所以f（b）-f（a）>0.

令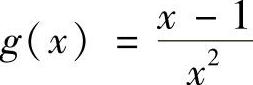，则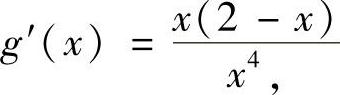，显然x=2是g（x）在（1，+∞）上的唯一驻点.因为当x>2时，g′（x）<0；当1<x<2时，g′（x）>0，所以x=2是g（x）的最大值点.于是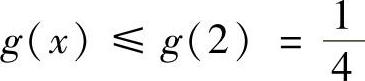，从而原不等式成立.

类题　设x>0，证明：2arctanx<3ln（1+x）.

提示　原不等式等价于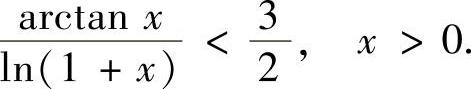

∀x>0，在[0，x]上应用柯西中值定理，∃ξ∈（0，x），使得

剩下的仿照例题证明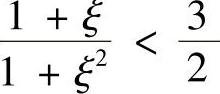，ξ>0即可.

另外，本题若令f（x）=3ln（1+x）-2arctanx，利用单调性证明更为简单！

例8.25　求出使不等式a^x>x^a（x>0）成立的一切正数a.

解　原不等式等价于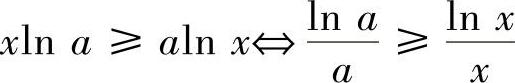，　x>0.

令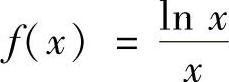，则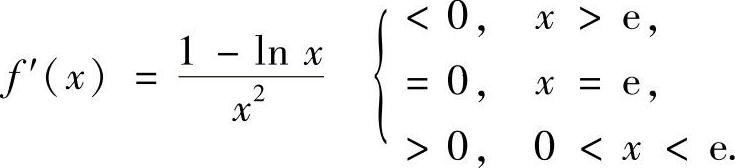

由此可知x=e是f（x）在（0，+∞）上的唯一极大值点，所以它是最大值点，最大值为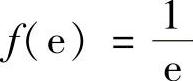.欲使原不等式成立，只要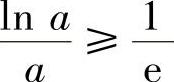即可.从而使原不等式成立的一切正数a适合条件：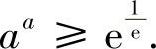

类题1　求实数α的范围，使得对任何正数x，y都成立下面的不等式：

提示　固定x，令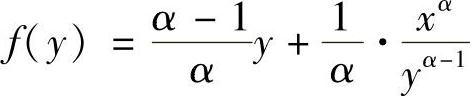，则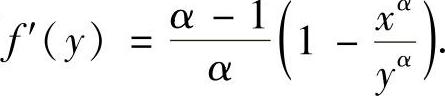当α>1时，y=x为最小值点，此时等式成立；当α=1时，不等式显然成立；当α<1时，y=x为最大值点，此时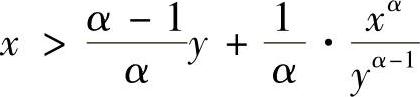，即原不等式不成立.

类题2（1）设α>0，β>0，证明：

（2）设0<x<1，证明：.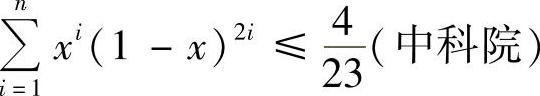

提示 （1）求被积函数f（x）=x^α（1-x）^β在[0，1]上的最大值，即得结论.

（2）令f_i（x）=xⁱ（1-x）²ⁱ，求f_i（x）在（0，1）内的最大值即可.

例8.26　设a，b>0，证明不等式：

（华中科技大学）.

分析　a与b在不等式中的地位是同等的，因此如果令x=1-t，则可将原不等式化为与之等价的形式：

进而，又可等价地化为：

证明　记f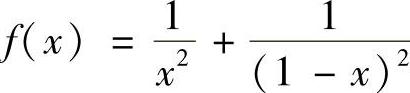，0<x<1，由于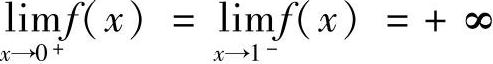，所以f（x）在（0，1）上的最小值必在内部取到.

令f′（x）=0可得驻点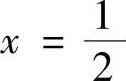，注意到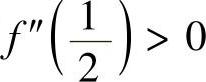，所以f（x）在（0，1）内的最小值为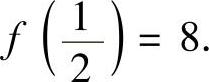

再记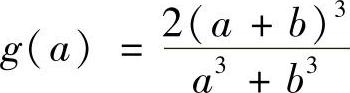，a≥b>0，则有

由此可知，g（a）在[b，+∞）上单调递减，即g（a）在[b，+∞）上的最大值在a=b处取到，且g（a）=8.

综上，我们完成了不等式的证明.

说明：本题将a，b视为常数，直接用单调性方法证明并不困难.在这里，我们主要是为了介绍方法.

例8.27　求最小的β和最大的α，使对所有的自然数n，有

（北师大；中科院）

证明　由于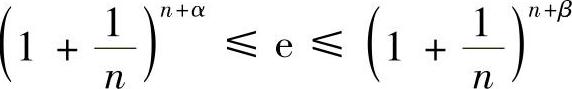，∀n∈N+

因此

将离散变量换成连续变量.令

下证：f（x）在（0，1]上严格单调递减，因而

事实上，

令 g（x）=（1+x）[ln（1+x）]²-x²，则

由此可见，g′（x）严格↓.由g′（0）=0可推出g′（x）<g′（0）=0，∀x∈（0，1].这表明g（x）严格↓，又由g（0）=0推出g（x）<0，∀x∈（0，1]，从而f′（x）<0，即f（x）在（0，1]上严格↓.于是有

类题 证明：集合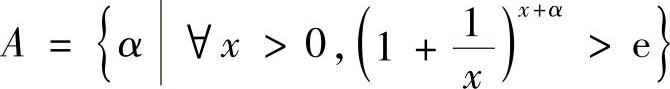有最小值，并求其最小值（北师大）.

提示 不等式

记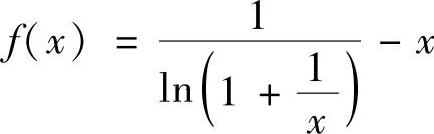，则α∈A是f（x）在x>0的上界.于是

由于f′（x）>0，所以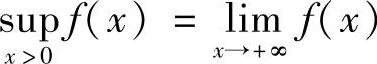.利用泰勒展开不难算出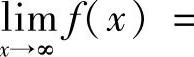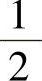，故.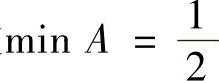

例8.28 求最小实数C，使得满足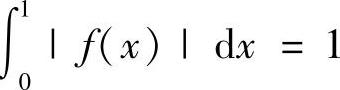的连续函数f（x）都有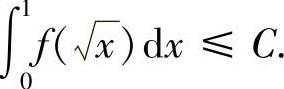（第四届全国大学生数学竞赛（非数学类）预赛试题）

证明 一方面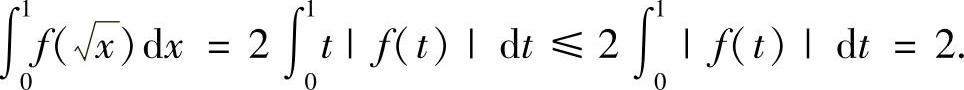，另一方面，如果取f_n（x）=（n+1）xⁿ，则有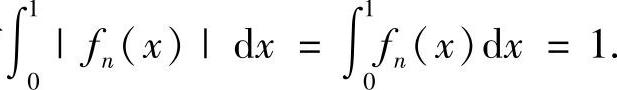而

由此可知，最小实数C=2.