
例8.1 平均值不等式 对任意n个正数a1,a2,…,an,有
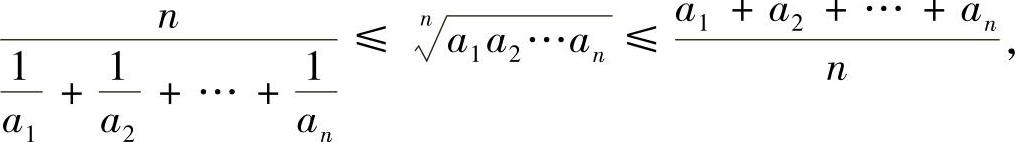
当且仅当a1,a2,…,an都相等时,等号成立.
简单地说,调和平均值≤几何平均值≤算术平均值.
证明 先证明右边的不等式成立.用数学归纳法.
当n=1,2时,不等式显然成立.
当n=2k(k∈N+)时,不等式是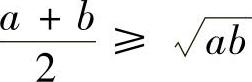 的直接推论.
的直接推论.
当n≠2k时,取l∈N+,使2l-1<n<2l.记
在a1,a2,…,an后面加上(2l-n)个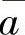 ,将其扩充成2l个正数.对这个2l个正数应用已证得的不等式,可得
,将其扩充成2l个正数.对这个2l个正数应用已证得的不等式,可得
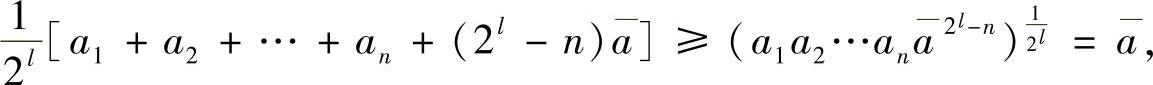
即
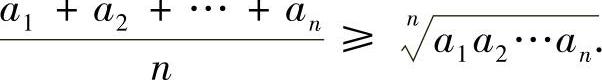
对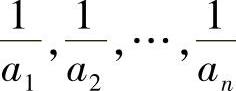 使用上面的结论,便可得左边的不等式.
使用上面的结论,便可得左边的不等式.
这个不等式也可用lnx在(0,+∞)上的凸性来证明.
例8.2 设f1,f2,…,fn为[0,1]上的非负连续函数.求证:存在ξ∈[0,1],使得
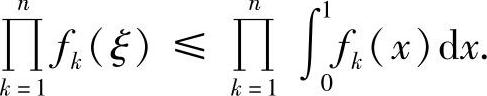
证明 记
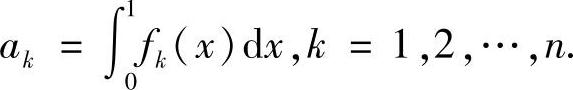
若有某个ak=0,则结论显然成立.
设ak>0(k=1,2,…,n).由平均值不等式,有
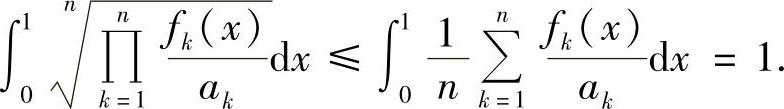
再由积分中值定理,存在ξ∈[0,1],使得
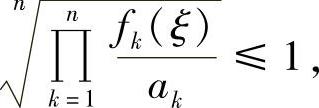
结论得证.
例8.3 施瓦茨(Schwarz)不等式 设f(x),g(x)在[a,b]上可积,则
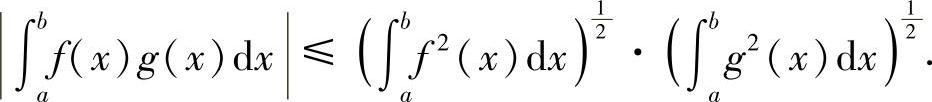
证明 设 ,对任意实数λ则有
,对任意实数λ则有
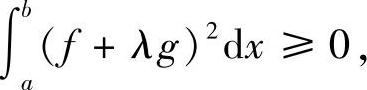
即
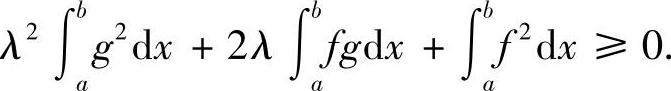
由实数λ的任意性,故其判别式Δ≤0,即
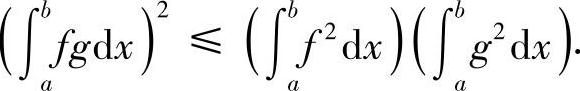
若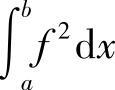 与
与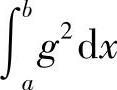 同时为零,则由不等式
同时为零,则由不等式
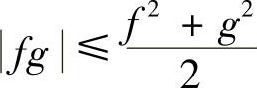
可知,
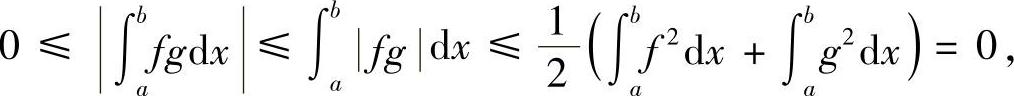
此时不等式变成等式,当然成立.
注8.1 这个不等式也称柯西-施瓦茨不等式.它的离散形式是

利用例8.3可很快捷地证明下面的结论.
类题1 设f(x)在[a,b]上可积,则
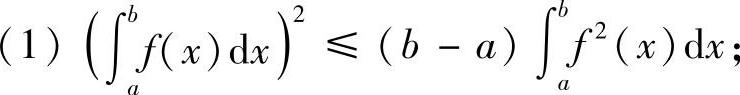
(2)当f(x)>0时,有
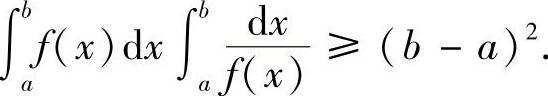
提示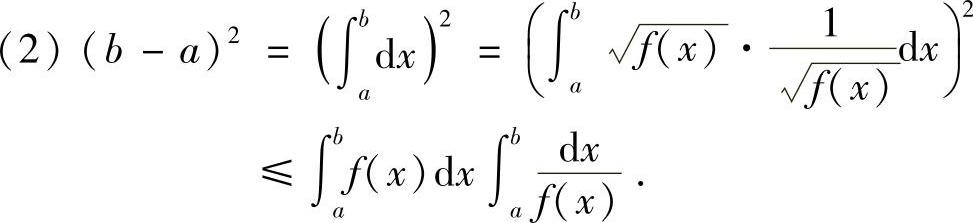
若f(x)在[a,b]上连续,也可用二重积分来证明.
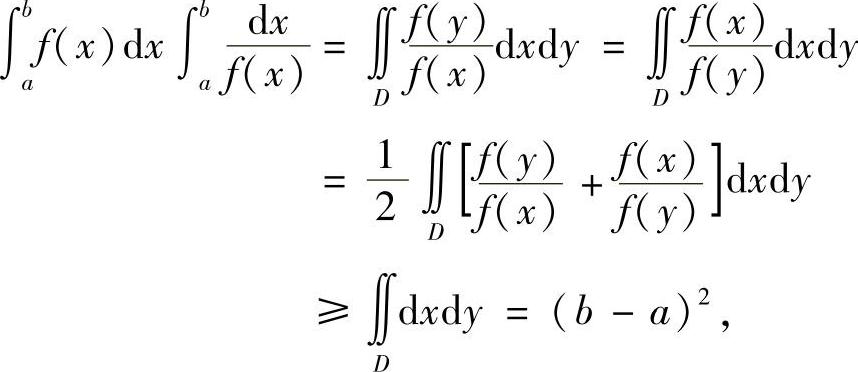
其中D=[a,b]×[a,b].
类题2 已知f(x)≥0在[a,b]上连续,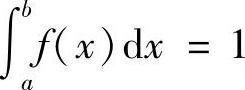 ,k为任意实数,证明:
,k为任意实数,证明:

(中国科大).
类题3 设f(x)在[a,b]上连续可导,f(a)=f(b)=0,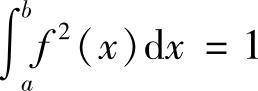 ,证明:
,证明:

提示 由施瓦茨不等式
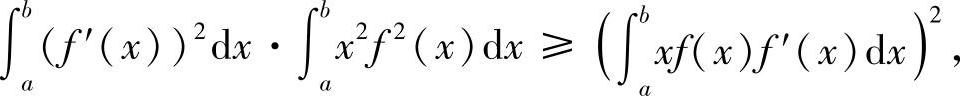
然后分部积分即可.
例8.4 设f(x)在[a,b]上有连续的导函数,f(a)=0,证明:
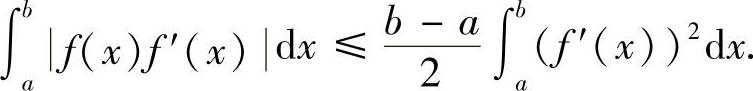
证明 令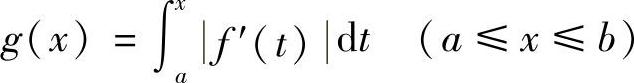 ,则g′(x)=f′(x).由f(a)=0可知,
,则g′(x)=f′(x).由f(a)=0可知,
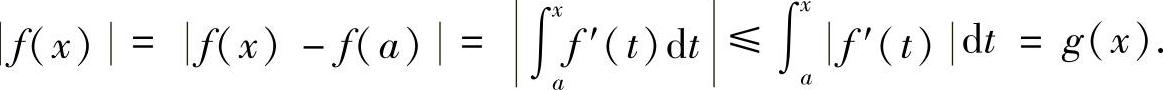
于是有
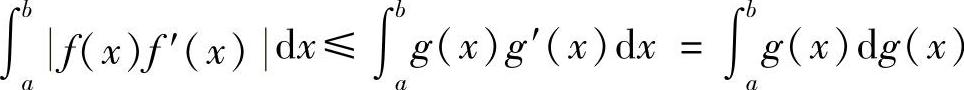
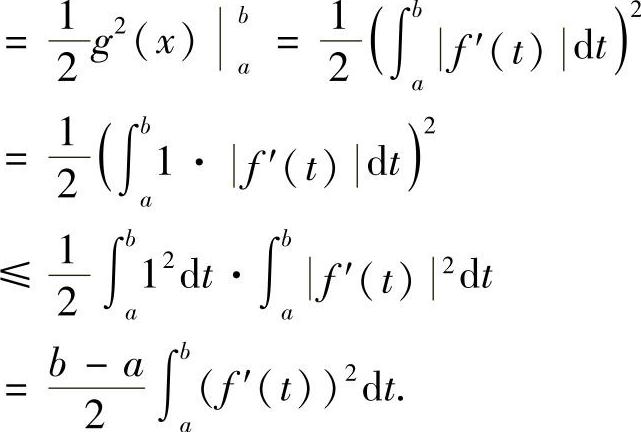
例8.5 杨格(W.H.Young)不等式 设y=f(x)是[0,+∞)上的严格单调递增的连续函数,f(0)=0,x=g(y)是它的反函数,a,b≥0,则(www.xing528.com)
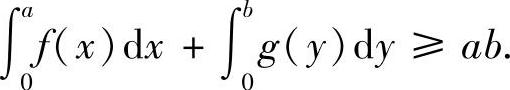
证法1 利用几何直观来证.若ab=0,则不等式显然成立.
不妨设a,b>0,分三种情形证明:
(1)若b=f(a),则显然有
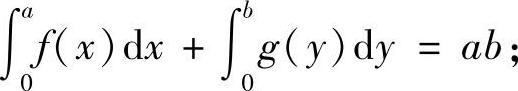
(2)若b>f(a),记f(a)=c,则0<c<b,且有
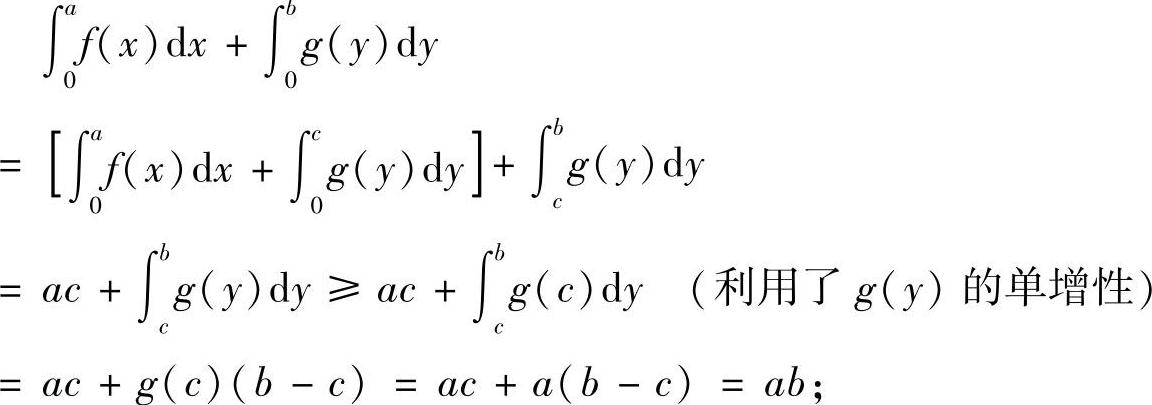
(3)若b<f(a),此时a>g(b),类似于(2)可证.
杨格不等式的几何示意图如图8-1所示.
证法2 用分析法来证.仅证b=f(a)的情形.
因为f(x)在[0,a]上单调递增且连续,故其反函数x=g(y)在[0,b]上单调递增且连续.将区间[0,a]n等分,
T: 0=x0<x1<x2<…<xn=a,
相应地点yi=f(xi)(i=0,1,…,n)构成区间[0,b]的一个分割
T′: 0=y0<y1<y2<…<yn=b.
因为f(x)在[0,a]上连续,所以它在[0,a]上一致连续,故当n→∞,即‖T‖→0时,有
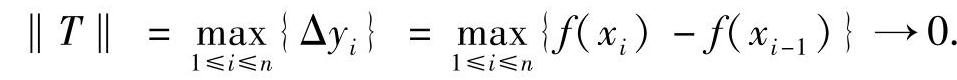
于是,由定积分的定义,得

至于b>f(a)与b<f(a)的情形用与证法1相同的思路.
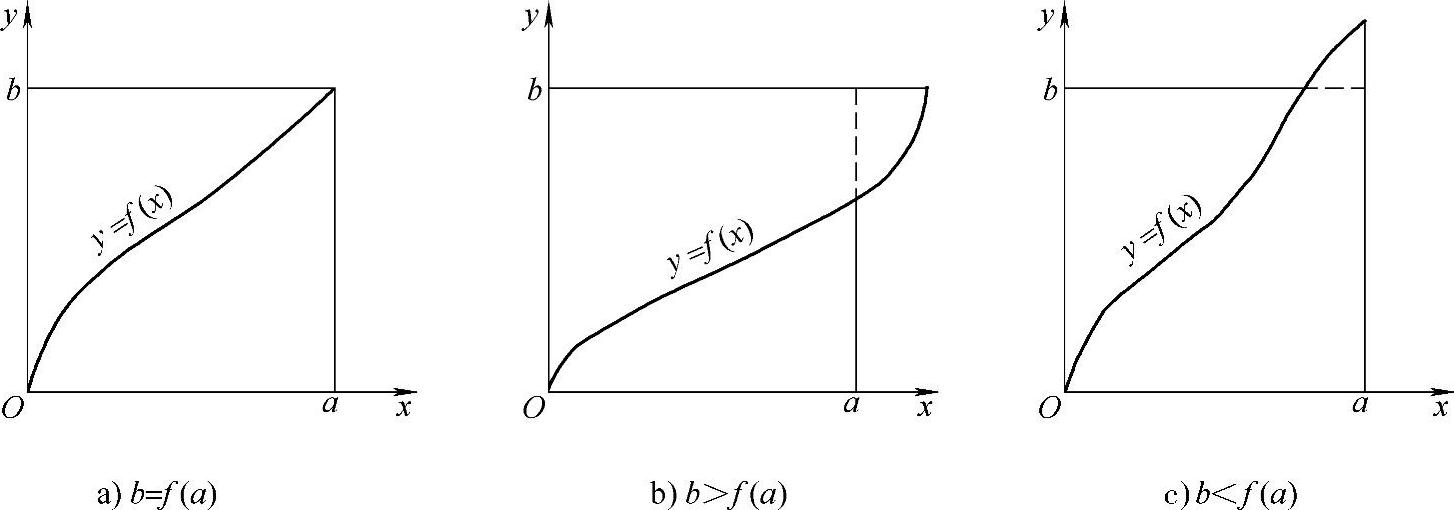
图 8-1
简单推论 设f(x)在[0,+∞)上严格单增且连续,f(0)=0,a,b≥0,证明:
ab≤af(a)+bf-1(b).
下面给出杨格不等式的两个应用.
例8.6 设a,b>0,p>1,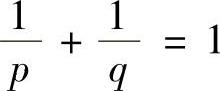 ,证明:
,证明:
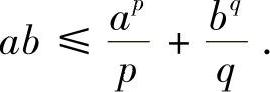
证明 因为p>1,所以f(x)=xp-1在[0,+∞)上严格单增且连续,其反函数为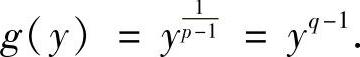 由杨格不等式,有
由杨格不等式,有
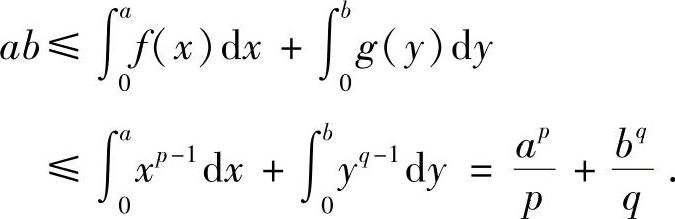
另外,若令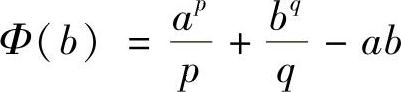 ,求出Φ(b)的最小值点,利用最值法也可证该不等式.
,求出Φ(b)的最小值点,利用最值法也可证该不等式.
类题1 设a,b>0,p>1,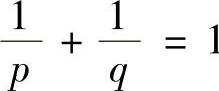 ,证明:
,证明:
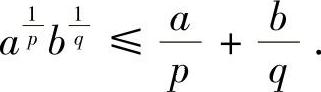
提示 在例8.6中,将a换成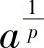 ,b换成
,b换成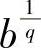 或在杨格不等式中取f(x)=xp-1,此时g(y)=yq-1,并将a换成
或在杨格不等式中取f(x)=xp-1,此时g(y)=yq-1,并将a换成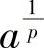 ,b换成
,b换成 即可.
即可.
类题2 设a,b>0,p>1,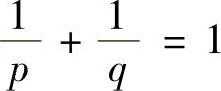 ,证明:∀ε>0,有
,证明:∀ε>0,有
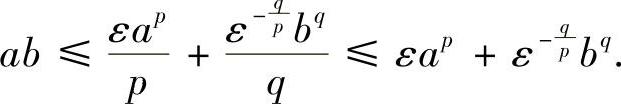
例8.7 设a,b≥1,证明不等式:
ab≤ea-1+blnb.
证明 取f(x)=ex-1,则f(x)在[0,+∞)上严格单增且连续,其反函数g(y)=ln(1+y).利用杨格不等式,可得
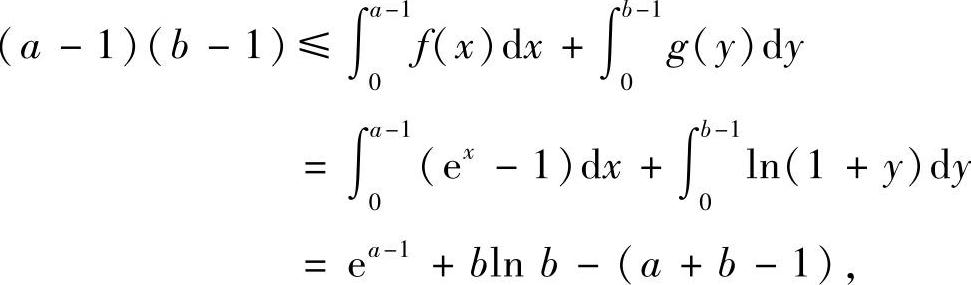
即
ab≤ea-1+blnb.
例8.8 赫尔德(Hölder)不等式 设f(x),g(x)在[α,β]上可积,p,q>1且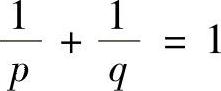 ,则
,则

当p=q=2时,该不等式即为施瓦茨不等式.
证明 先设f,g是[α,β]上的非负可积函数.
如果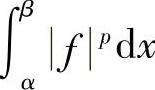 与
与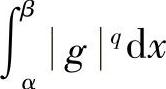 之一为零,不妨设
之一为零,不妨设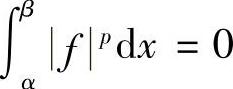 ,则此时赫尔德不等式右边为零,我们将证明左边也为零.
,则此时赫尔德不等式右边为零,我们将证明左边也为零.
事实上,设0≤f(x),g(x)≤M,x∈[α,β].由可积性条件,∀ε>0,η>0,存在[α,β]的分割T,使得分割T中满足fp(x)≥εp的区间长度之和不超过η.并且当分割细度充分小时,有
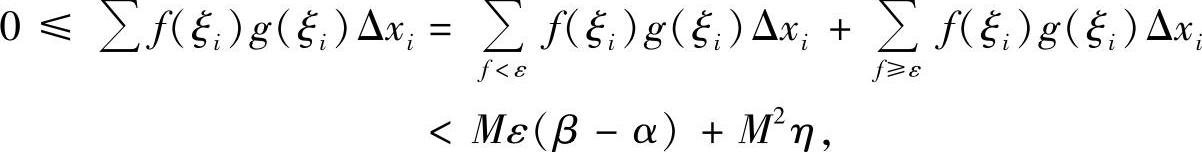
故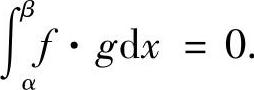
如果 ,
,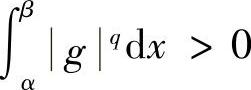 ,则令
,则令
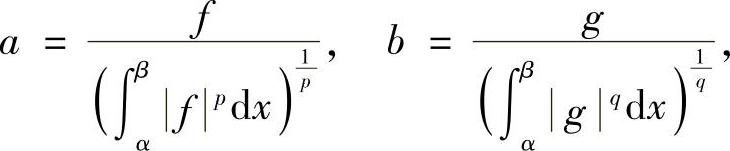
显然a,b≥0.由例8.6的不等式,有
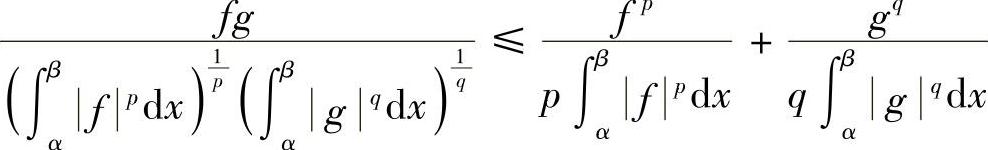
对上式两边从α到β积分,并注意到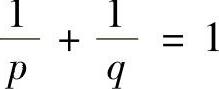 可得结论.
可得结论.
当f,g变号时,由不等式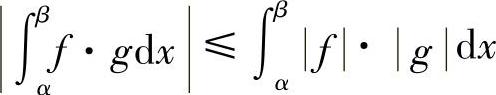 ,利用已证得的结论可知赫尔德不等式也成立.
,利用已证得的结论可知赫尔德不等式也成立.
注8.2 赫尔德不等式的离散形式:设ak,bk(k=1,2,…,n)是两组正实数,p,q>1,且 ,则
,则
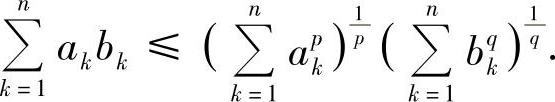
当p=q=2时,上述不等式就是柯西-施瓦茨不等式.
例8.9 试证明:
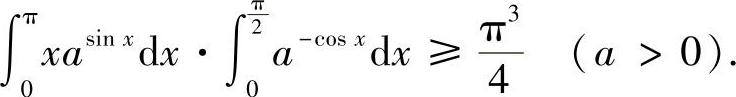
证明 令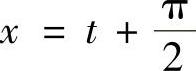 ,则
,则
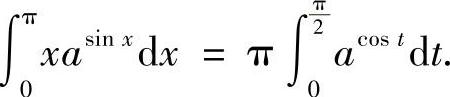
于是原不等式左边变为
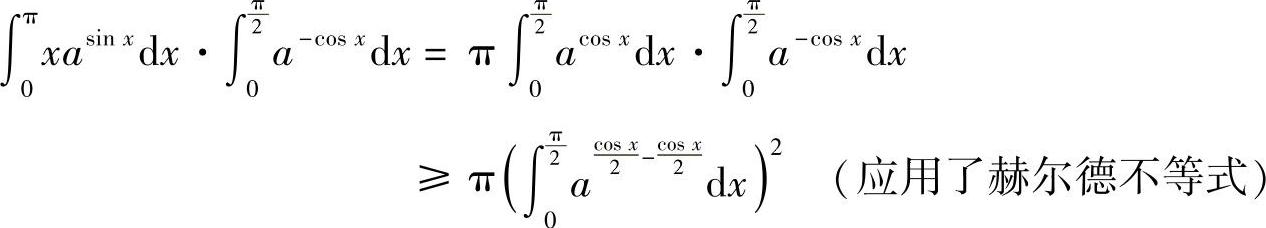
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




