曲线积分关系考研数学分析整理真题精选

坐标微元dr=τds，其中τ为曲线沿指定方向的单位切向量，则

对平面曲线L，设cosα，cosβ为它的切方向余弦，则

若用n表示曲线L的外法向，用（x，n）表示x轴正向与n的夹角，则cosα=-sin（x，n），　sinα=cos（x，n）.

于是又有

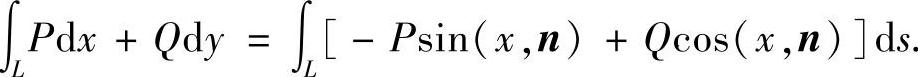
对空间曲线L，设cosα，cosβ，cosγ是切方向余弦，则

例7.49　计算，其中L为球面x²+y²+z²=R²与平面x+y+z=0的交线.

解法1　（用参数方程求解）.将z=-x-y代入球面方程整理可得

令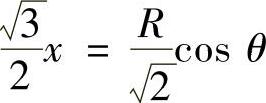，代入上式得：，所以

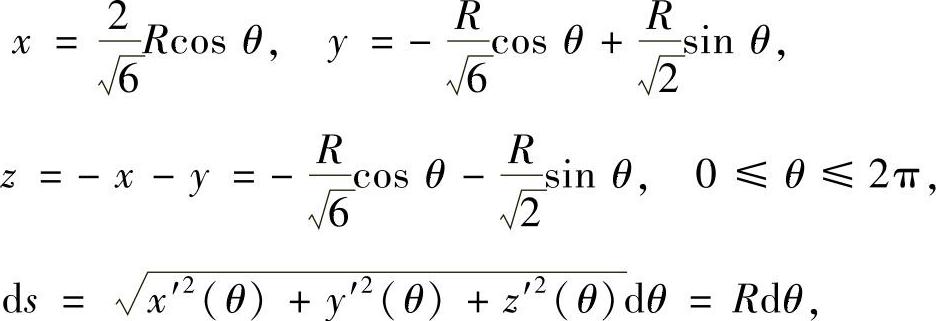
于是

解法2　（用对称性求解）.由于积分变量x，y，z在曲线方程中具有轮换对称性（即三个变量轮换位置，曲线方程不变），所以

故

类题1　计算，其中L是球面x²+y²+z²=R²与平面x+y+z=0的交线.

提示　可直接利用参数方程求解，但利用对称性更为简单.由

可得

类题2　计算曲线积分，其中L是椭圆周，方向为逆时针方向.

提示　曲线L位于x轴上、下方的部分分别记为L₁、L₂，显然L₁与L₂关于x轴对称，且走向相反.由于关于y是偶函数，所以

同理，从而I=0.

例7.50　求八分之一球面x²+y²+z²=R²，x≥0，y≥0，z≥0的边界曲线的重心.设曲线的线密度ρ=1（数学Ⅱ）.

解　设边界曲线L在xOy，yOz，zOx平面内的弧段分别为L₁，L₂，L₃，则曲线的重量为

设曲线L的重心坐标为，则

由对称性知，，故所求的重心为

例7.51　计算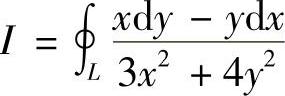，其中L是椭圆2x²+3y²=1，方向沿逆时针方向.

解 ，在任何不包含原点的区域内均有，因此对任何完全落在L内部且包含原点的封闭曲线C，在L和C所夹的区域内应用格林公式，有

其中C^-表示在曲线C上方向沿顺时针方向.

由此可得

选取ε>0适当小，使C：3x²+4y²=ε²完全落在L内，则有

注7.8　本例的解法是利用积分与路径的无关性来处理内部含有奇点的第二型曲线积分常用的方法.另外，需要提醒大家的是，要注意题设的条件.例如，当f（u）连续时，证明

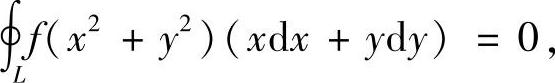
（其中L是一光滑封闭曲线）就不能使用.此时只能使用积分与路径无关的另一个条件，即Pdx+Qdy是某个函数的全微分.

类题　证明：

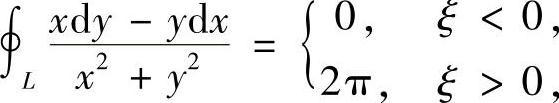
其中L是以（ξ，1），（ξ，-1），（-1，-1），（-1，1）为顶点的矩形边界，积分沿L的正向.

例7.52　计算曲线积分，其中

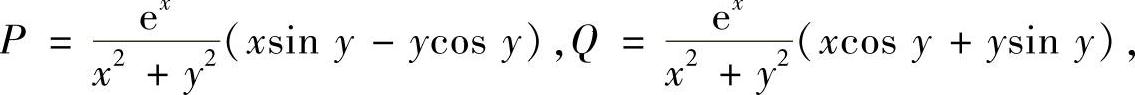
L是绕原点的简单闭曲线.

解法1　当x²+y²≠0，可以验证，所以可将曲线L换成以原点为中心，适当小的ε>0为半径的小圆周：

L′：x=εcosθ，y=εsinθ，0≤θ≤2π.

易见

构造辅助函数.

仍有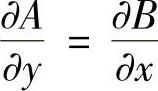.若定义A（0，0）=0，B（0，0）=1，则A，B在原点连续.

事实上，由泰勒展开式，有

所以有

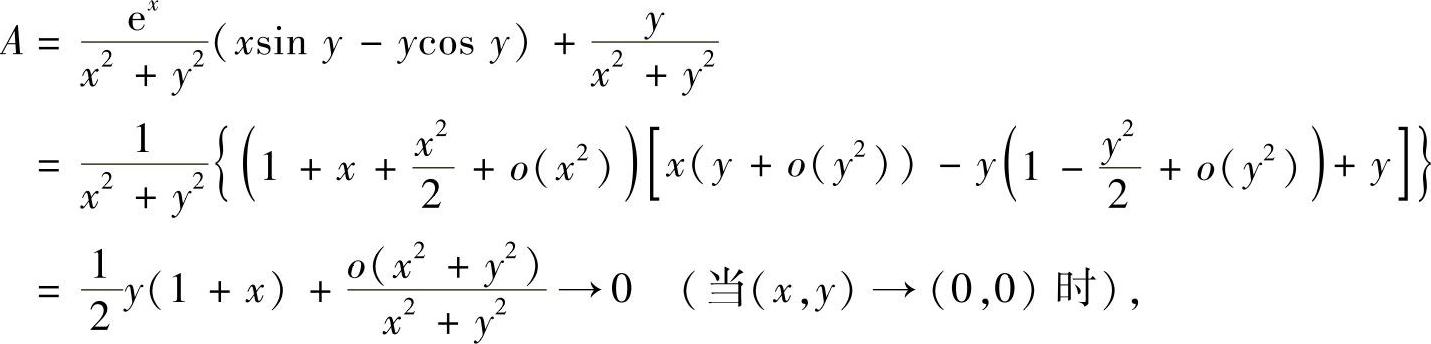
即补充定义后A在原点连续.同理可证B也在原点连续.于是

I=J=2π

解法2　在L′上，有

故

积分值与ε无关.注意到被积函数关于ε，θ连续，令ε→0+，在积分号下取极限可得

例7.53　设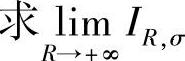，（浙大）.

解　记椭圆周x²+xy+y²=R²为L，取ε>0充分小，使小圆Γ：x²+y²=ε²完全落在L内.并记L与Γ所夹的区域为D，由格林公式，则有

对J₁作极坐标变换：x=ρcosθ，y=ρsinθ，则

对J₂利用参数方程：x=εcosθ，y=εsinθ，则

J₂=2πε^2-2σ.

于是

注意到

所以

例7.54　计算曲线积分，其中L是曲线，从z轴的正向往负向看去L的方向是顺时针方向（数学Ⅰ）.

解法1　（用参数方程求解）　令x=cost，y=sint，则

z=2-cost+sint.

故

解法2　（用斯托克斯公式求解）　设S为平面x-y+z=2上以L为边界的有限部分，其法向量与z轴正向的夹角为钝角.D_xy为S在xy平面的投影域，即D_xy：x²+y²≤1.记F={z-y，x-z，x-y}，则

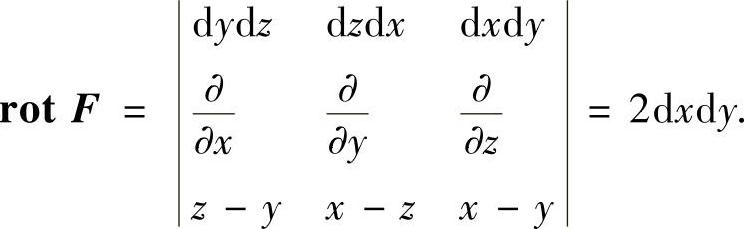
由斯托克斯公式可得

其中dr={dydz，dzdx，dxdy}.

注7.9　在使用斯托克斯公式将空间曲线积分化成第二类曲面积分（当然也可化成第一类曲面积分，关于这些在下一段我们详细讲解）时，要注意L的方向和曲面S的法向量符合右手法则.

例7.55　设封闭曲线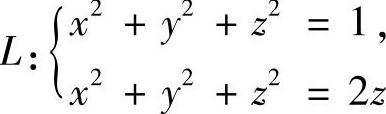的正向与z轴正向符合右手法则，求曲线积分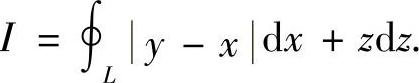

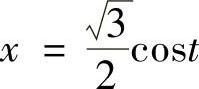解　由可得因此可设曲线L的参数方程为：，，，t从到3

于是

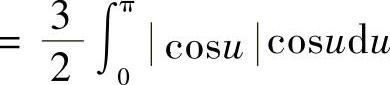
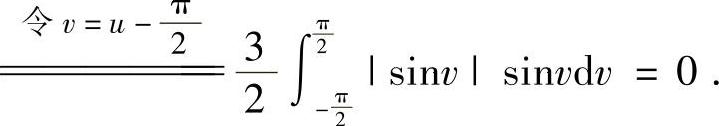
注7.10（1）由于被积函数中出现了y-x，所以本例不能使用斯托克斯公式；

（2）参数t的取值从到是为了让后面定积分的积分区间化成对称区间.当然也可以取t的值为-π到π或0到2π等.

例7.56　计算曲线积分，其中L是从点（a，0，0）沿着以下曲线到点（0，0，c）的路径：，（a>0，b>0，c>0为常数），x≥0，y≥0，z≥0（复旦）.(https://www.xing528.com)

解法1　（用参数方程求解）.从中解出代入椭球面方程，整理可得：

令

则

由于x≥0，y≥0，z≥0，并注意到椭圆心在处，所以0≤θ≤π，故

解法2　（选取z作为参数）.曲线L的参数方程为：

于是有

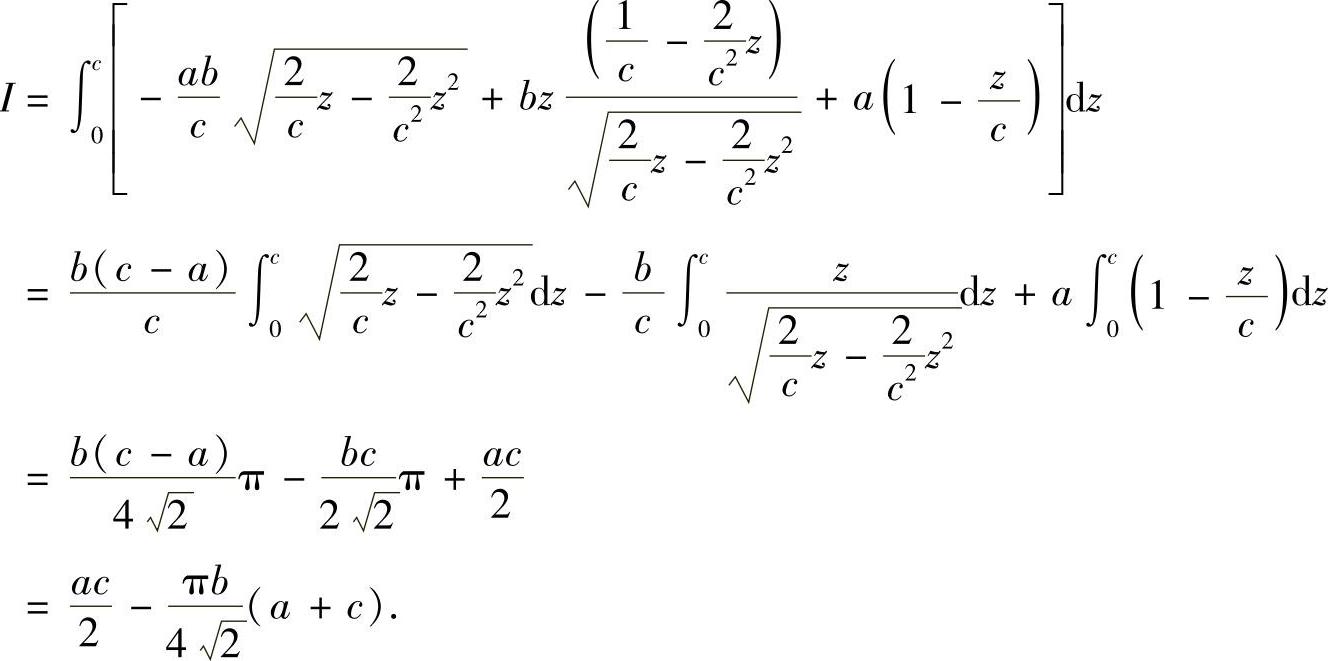
解法3　（用斯托克斯公式求解）.由于空间曲线L不是闭曲线，所以补充直线段L₁，使得L+L₁为闭曲线，其中L₁是从点（0，0，c）沿直线到点（a，0，0）的直线段.由斯托克斯公式，有

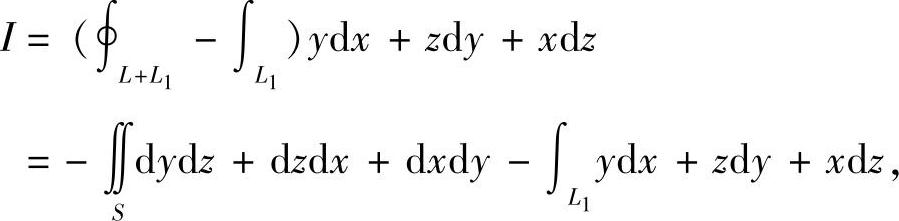
其中S是由L+L₁所围的有限部分.

注意到S在xOy平面、yOz平面以及zOx平面的投影分别为：

及

所以

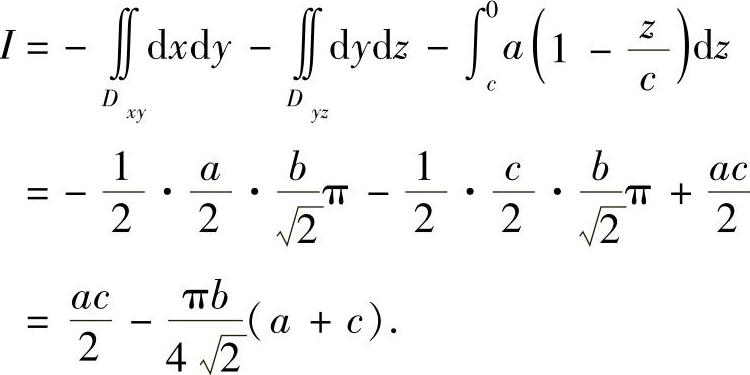
例7.57　设函数f（x）在（-∞，+∞）上具有一阶连续导数，L是上半平面y>0内的有向分段光滑曲线，其起点为（a，b），终点为（c，d）.记

（1）证明：曲线积分I与积分路径无关；

（2）当ab=cd时，求I的值.

（数学Ⅱ）.

证明　（1）因为

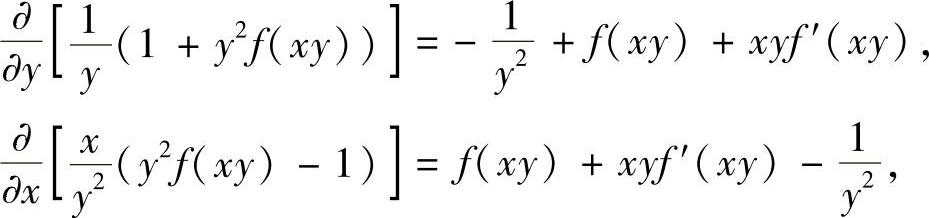
所以在上半平面内曲线积分I与积分路径无关.

解　（2）由（1）知，是某个函数u（x，y）的全微分，而

设F（x）是f（x）的一个原函数，则，因此

类题1　设曲线积分与积分路径无关，其中φ（x）具有连续导数，且φ（0）=0，计算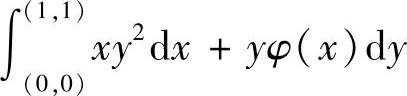（数学Ⅰ）.

类题2　设函数Q（x，y）在xy平面上具有一阶连续偏导数，曲线积分与积分路径无关，并且对任意t恒有

求Q（x，y）（数学Ⅰ，Ⅱ）.

提示　由已知条件：，即Q（x，y）=x²+c（y），c（y）为待定函数.又

让两者相等，并两边关于t求导可得c（t）=2t-1，故Q（x，y）=x²+2y-1.

或由

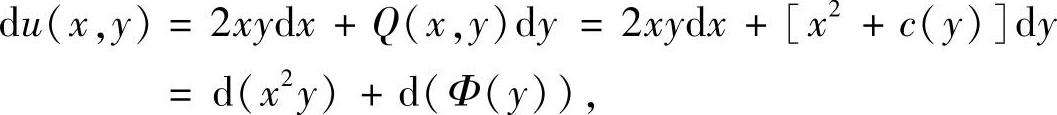
可得

u（x，y）=x²y+Φ（y），

其中Φ（y）是c（y）的一个原函数.

又由

可知，

Φ（t）=t²-t+Φ（1）.

两边关于t求导可得

c（t）=2t-1.

例7.58　质点P沿着以AB为直径的圆周，从点A（1，2）运动到点B（3，4）的过程中受变力F作用，如图7-5所示.F的大小等于质点P到原点O之间的距离，其方向垂直于线段OP且与y轴正方向的夹角小于，求变力F对质点P所做的功（数学Ⅰ）.

解　设P点的坐标为（x，y）.由题设，

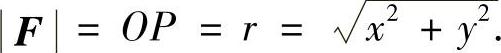
图7-5　例7.58图

设r₀=（cosα，sinα），则r₀可表示为

由题设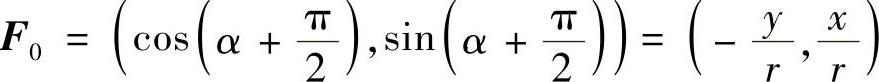，（F₀是F方向的单位向量），故F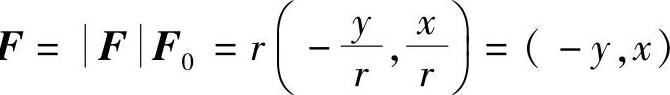.于是变力F对质点P所做的功为

由于的方程为（x-2）²+（y-3）²=2，所以的参数方程可表示为：，，　t从到.从而

类题　设质点受力作用，力的反方向指向原点，大小与质点离原点的距离成正比.若质点从点（a，0）沿椭圆移动到点（0，b），a，b>0.求力所做的功（北京航空航天大学）.

提示　由题意，F=（kx，ky），则

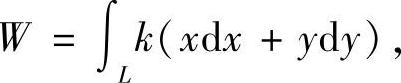
其中L是从点（a，0）到点（0，b）的椭圆段.

例7.59　计算积分

其中（n，x），（n，y）分别是由x轴、y轴正向与L的外法向n之间的夹角，L为逐段光滑的简单闭曲线.

解　L⁺表示L的正向，即沿逆时针方向，切线方向τ与L+一致，如图7-6所示.从n逆时针旋转即到τ，于是有

（n，x）=（τ，y），（n，y）=π-（τ，x），

故

cos（n，x）ds=cos（τ，y）ds=dy，

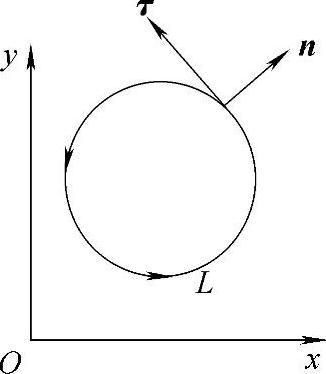
图7-6　例7.59图

cos（n，y）ds=-cos（τ，x）ds=-dx.

从而

其中S表示L所围的面积.

类题　计算高斯积分

其中D表示单连通区域D的边界，r为D上一点P（x，y）到D外一点A（ξ，η）的距离，（r，n）为r（即向量）与外法向n的夹角.

提示　因为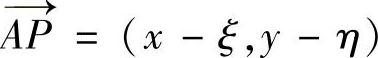，n=（cos（n，x），cos（n，y）），所以

于是

当A在D外部时，由格林公式可得I=0.

当A在D内部时，取含于D内的以A点为圆心的小圆C，则

例7.60　已知平面区域D={（x，y）0≤x≤π，0≤y≤π}，L为D的正向边界.试证：

（数学Ⅰ）.

证法1　（1）由于

所以欲证的等式成立.

（2）由（1），利用平均值不等式得

证法2　（1）由格林公式，有

因为D关于直线y=x对称，所以左边=右边.

（2）由（1）得