【摘要】：第二型曲线积分的背景是质点受力作用沿曲线运动所做的功的计算，因此这类曲线积分与方向（即起、终点）有关.这样凡是用不等式表示的性质对第二型曲线积分均不再成立，由此可推出积分的中值性也不再成立.但定积分的其他性质如线性性、可加性等对第二型曲线积分仍然成立.（1）计算方法第二型曲线积分计算的基本方法是：化为定积分.积分的下限对应曲线L的起点，上限对应曲线L的终点.若t=α对应曲线L的起点A，t=β对应曲
第二型曲线积分的背景是质点受力作用沿曲线运动所做的功的计算，因此这类曲线积分与方向（即起、终点）有关.这样凡是用不等式表示的性质对第二型曲线积分均不再成立，由此可推出积分的中值性也不再成立.但定积分的其他性质如线性性、可加性等对第二型曲线积分仍然成立.
（1）计算方法
第二型曲线积分计算的基本方法是：化为定积分.积分的下限对应曲线L的起点，上限对应曲线L的终点.
若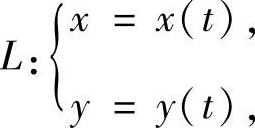
t=α对应曲线L的起点A，t=β对应曲线L的终点B，则
对空间曲线L也有类似的公式.
计算第二型曲线积分常用的方法：
1）利用曲线的参数方程化成定积分求解；
2）对平面曲线积分用格林公式化成二重积分求解；
3）对空间曲线积分用斯托克斯公式化成第一型曲面积分求解；
4）当积分与路径无关而只与起、终点有关时，用求原函数的方法求解.
另外利用对称性可以简化运算.(www.xing528.com)
对称性定理 设L为分段光滑的平面曲线.
1）若L=L1∪L2，L1与L2关于x轴对称，且走向相反，则
2）若L=L1∪L2，L1与L2关于y轴对称，且走向相反，则
（2）第二型曲线积分的应用
1）求变力做功
设质点在变力F（x，y）作用之下沿着曲线L从A点运动到B点，则变力所做的功为
2）求平面图形的面积
设L是逐段光滑的简单闭曲线，则它所围的面积S用曲线积分表示为：
其中曲线L的正向为逆时针方向.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
