(1)连续性定理 设f(x,y)在闭区域D=[a,b]×[c,d]上连续,则
在[c,d]上连续.
(2)积分次序交换定理 设f(x,y)在闭区域D=[a,b]×[c,d]上连续,则
(3)可微性定理 设f(x,y),fy(x,y)都在闭区域D=[a,b]×[c,d]上连续,则I(y)在[c,d]上可微,且在[c,d]上成立
又设a(y),b(y)在[c,d]上可微,满足a≤a(y)≤b,a≤b(y)≤b,则
在[c,d]上可微,且成立
注7.1 由于连续性和可微性刻画的都是函数的局部性质,所以将定理中闭区间[c,d]改为开区间(c,d)(c可以是-∞,d可以是+∞),相应地连续性定理和可微性定理的结论在(c,d)上仍成立.
但可积性刻画的是函数的整体性质,一般不能将闭区间改为开区间.例如,函数
在[0,1]×(0,1)上连续.易见
于是
类似地,有
这表明积分次序不能交换.
(4)求参变量积分常用的方法
如果直接求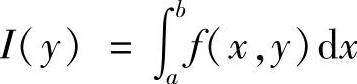 有困难,常用如下两种方法:
有困难,常用如下两种方法:
1)先求I′(y),即先求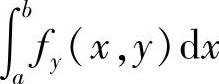 ,然后再对y积分求出I(y);
,然后再对y积分求出I(y);
2)把f(x,y)表示为积分形式,然后再交换积分的次序.
例7.1 求极限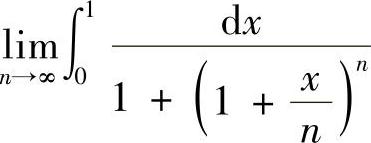 .
.
解 这个题目在第五讲中我们曾经用狄尼定理做过(见例5.30),在这里我们将用连续性定理来求解.
将离散变量n改成连续变量,即令
显然,f(x,y)在[0,1]×[0,1]上连续,由连续性定理,有
例7.2 设f(x)在[0,1]上连续,研究函数
的连续性.
解 显然F(t)在(-∞,+∞)上有定义.记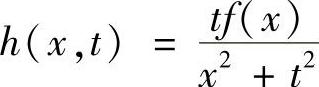 ,∀t0∈R且t0≠0.由于h(x,t)在[0,1]×[t0-δ,t0+δ](取δ>0适当小使0不属于[t0-δ,t0+δ])上连续,所以根据连续性定理F(t)在点t0处连续.
,∀t0∈R且t0≠0.由于h(x,t)在[0,1]×[t0-δ,t0+δ](取δ>0适当小使0不属于[t0-δ,t0+δ])上连续,所以根据连续性定理F(t)在点t0处连续.
下面讨论F(t)在t0=0处的连续性.先考虑
将积分分成两段来计算:(https://www.xing528.com)
而当t→0+时,
其中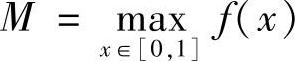 .因此,
.因此,
同理可证
由此可见,仅当f(0)=0时,F(t)在0点连续,否则在0点不连续.
例7.3 设a>0,b>0,求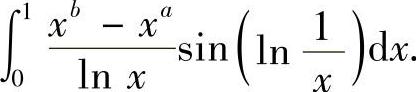
解 当x→1-和x→0+时,被积函数趋向于0,所以积分是正常积分.注意到
则原积分可写成
由于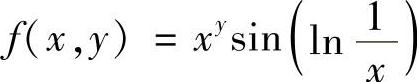 在[0,1]×[a,b](设a<b)上连续,所以积分次序可交换,即
在[0,1]×[a,b](设a<b)上连续,所以积分次序可交换,即
记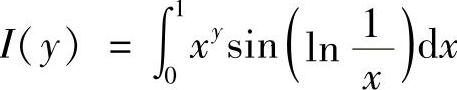 ,连续使用分部积分法可得
,连续使用分部积分法可得
即
于是
例7.4 计算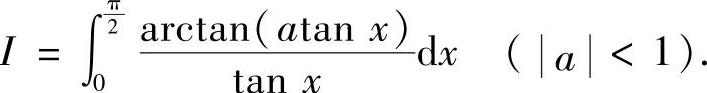
解 记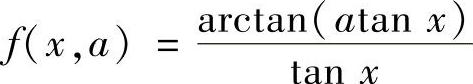 .因为
.因为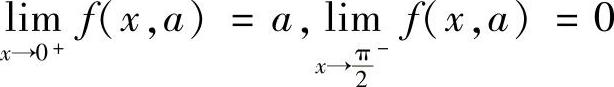 ,所以积分I为正常积分.若补充定义
,所以积分I为正常积分.若补充定义
则f(x,a)在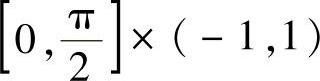 上连续.而显然
上连续.而显然
也在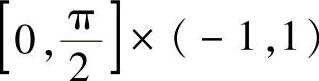 上连续.由可微性定理,有
上连续.由可微性定理,有
由于a=0时,I(a)=0,所以
当a≥0时,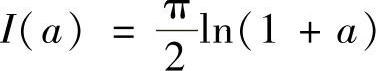 ;当a<0时,
;当a<0时,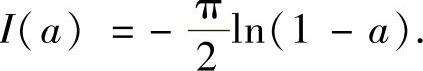
注7.2 从本例的求解过程可以看出,有时连续性条件并不满足,需要人为地补充个别点的定义,使之符合积分号下求导(求积分)的条件.
例7.5 设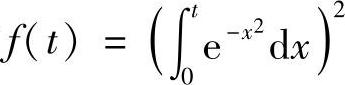 ,
,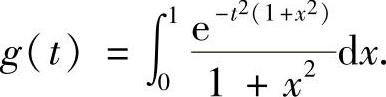 证明:
证明: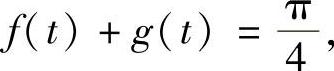 并由此计算
并由此计算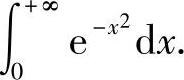
证明 由可微性定理,有
令xt=y,则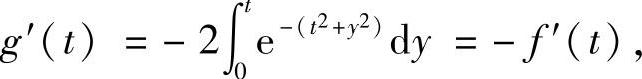 或
或
f′(t)+g′(t)=0.
对上式两边从0到t积分可得
令t→+∞,有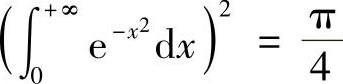 , 即
, 即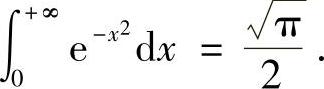
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




