极值和最值-考研数学分析复习

（1）无条件极值与最值

无条件极值

设f（x₁，x₂，…，x_n）是开区域D⊂Rⁿ上二次可微函数，P₀=（x⁰₁，x⁰₂，…，x⁰_n）∈D.若点P₀是f的一个极值点，由极值的必要条件有Δf（P₀）=0.根据泰勒公式有

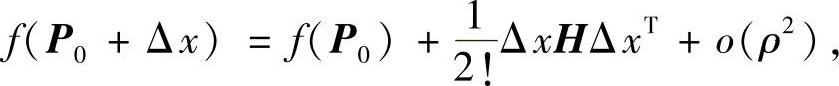
其中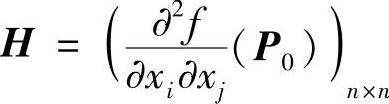称为海赛（Hesse）阵.由此可得到取得极值的充分条件：

1）若H正定，则f（P₀）是极小值；

2）若H负定，则f（P₀）是极大值；

3）若H不定（即既有正特征根，也有负特征根），则点P₀不是极值点；

4）若H半定（即所有特征根同号，但有零特征根），则需要作进一步判断.特别地，对二元函数f（x，y），如果f（x，y）在驻点（x₀，y₀）的某个邻域内有二阶连续偏导数，并记A=f_xx（x₀，y₀），B=f_xy（x₀，y₀），C=f_yy（x₀，y₀），Δ=AC-B²，则

1）若Δ>0，A>0（或C>0），则f（x₀，y₀）是极小值；

2）若Δ>0，A<0（或C<0），则f（x₀，y₀）是极大值；

3）若Δ<0，则（x₀，y₀）不是极值点；

4）若Δ=0，则需要作进一步判断.

注6.6　上面给出的极值充分条件只局限于特殊驻点P₀（即f在驻点P₀的某邻域内有二阶连续偏导数）.而对其他点（偏导数不存在的点、二阶偏导数不存在的驻点、二阶偏导数不连续的驻点）必须用别的方法来判断.

无条件最值

求多元函数的最值一般有以下四种方法（以二元函数为例）.

1）f（x，y）定义在有界闭区域D上.先求出D内的全部驻点和不可偏导点及相应的函数值，然后求f在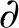D上的最值（可将边界曲线代入f（x，y）化为求一元函数的最值），最后比较这些函数值的大小.最大者为最大值，最小者为最小值；

2）f（x，y）定义在无界区域上.去掉明显不取最值的无界子区域，化成在剩余部分（即有界区域）上的最值问题；

3）f（x，y）定义在有界开区域上.先将f（x，y）连续延拓到D—上，然后在有界闭区域上求最值，最后求出所要的结果；

4）利用

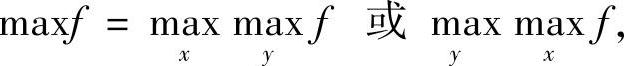
对x，y累次求最大值.

注6.7　对多元函数而言，唯一的极值点并不一定是最值点.例如，函数f（x，y）=x³-4x²+2xy-y²在R²有唯一的极大值点（0，0），但f（0，0）=0并不是f（x，y）在R²上的最大值.事实上，由

f（x，y）=x³-3x²-（y-x）².

可见，f（x，y）的最大值只能在直线y=x上取到，此时，f（x，x）=x³-3x².显然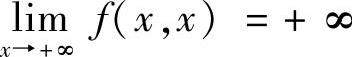，即f（x，x）无最大值.

但在实际问题中，如果所考虑的问题确有最值，而边界值明显不是最值，在区域内部驻点又唯一，则该驻点必是最值点.

（2）条件极值与最值

条件极值

目标函数f（x₁，x₂，…，x_n）在约束条件φ_i（x₁，x₂，…，x_n）=0（i=1，2，…，m，m<n）之下的极值问题，可归结为求拉格朗日函数

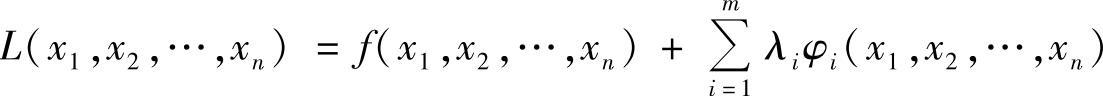
的无条件极值，其中λ_i（i=1，2，…，m）为常数因子，这种方法称为拉格朗日乘子法.

拉格朗日乘子法的具体步骤如下：

第一步：令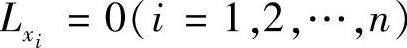与φ_i=0（i=1，2，…，m）联立解出L的全部驻点和λ_i的具体值（在许多情况下，可不解出λ_i的具体值），并要求在驻点处矩阵

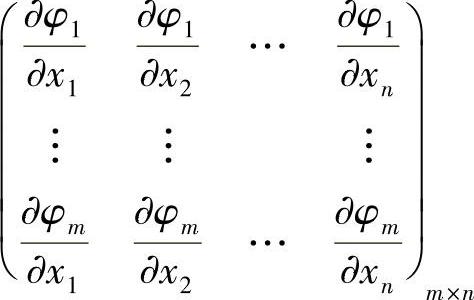
的秩为m（即要求m个约束条件是独立的）；

第二步：对每一个驻点P₀，算出海色阵.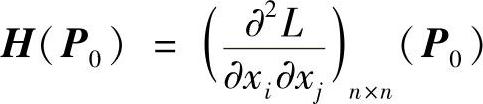

1）若H（P₀）正定，则P₀点为（条件）极小值点；

2）若H（P₀）负定，则P₀为（条件）极大值点；

3）若H（P₀）既不正定，也不负定，则由

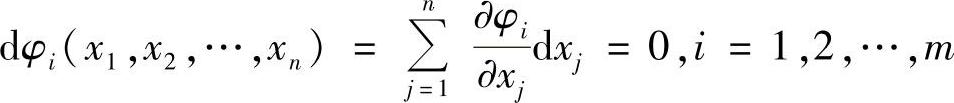
可解出dx₁，dx₂，…，dx_n中的m个因为矩阵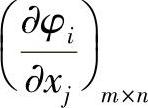的秩为m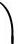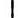.不妨设解出的是dx₁，dx₂，…，dx_m，将它们代入n元二次型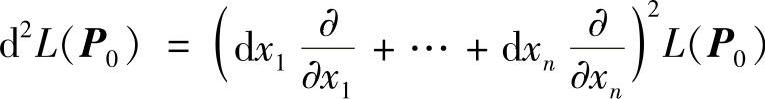中，化为（n-m）元二次型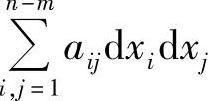.令A=（a_ij）（n-m）×（n-m）.

（3-1）若A正定，则P₀点为（条件）极小值点；

（3-2）若A负定，则P₀点为（条件）极大值点；

（3-3）若A不定，则P₀点不是（条件）极值点；

（3-4）若A半定，则需要作进一步判断.

条件最值

条件最值可通过比较条件极值、边界最值、不可偏导点的值以及二阶偏导数不存在点的值来得到.但由于确定条件极值比较麻烦，所以条件最值的求法也是很烦琐的！

（3）隐函数的极值

求隐函数的极值有两种方法：（1）直接从方程出发，求出驻点，并利用求无条件极值的方法判断驻点是否为极值点，从而求出极值.这种方法叫直接法；（2）化为条件极值，并利用求条件极值的方法求出极值.这种方法叫间接法.

例6.37　在什么条件下，方程组

x=f（u，v），y=g（u，v），z=h（u，v），F（u，v）=0（1）

能在O-xyz空间代表一空间曲线？在怎样的点

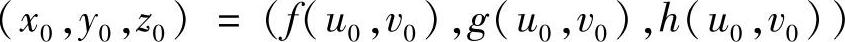
处可求切线？写出切线方程和法平面方程.

解　在所给的方程组中，若能由F（u，v）=0确定一个隐函数，例如v=v（u），则x=x（u）=f（u，v（u）），y=y（u）=g（u，v（u）），z=z（u）=h（u，v（u））表示一空间曲线（实际上是空间曲线的一部分）.为此，假设F_u，F_v在点（u₀，v₀）的某邻域内连续，且F（u₀，v₀）=0，F_v（u₀，v₀）≠0.此时有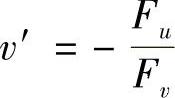，故当

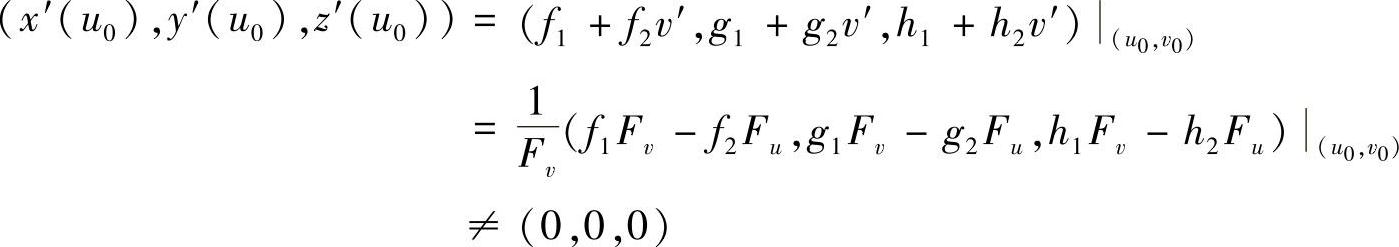
时，在点（x₀，y₀，z₀）=（f（u₀，v₀），g（u₀，v₀），h（u₀，v₀））的某邻域内，方程组（1）能代表唯一的一条通过点（x₀，y₀，z₀）的曲线，且在该点可求切线.

切线方程和法平面方程分别为：

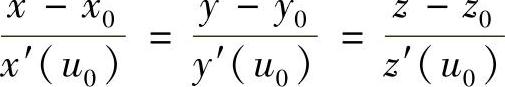
和

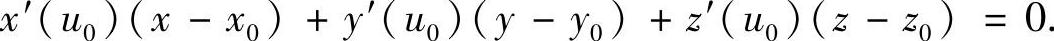
例6.38　求空间曲线

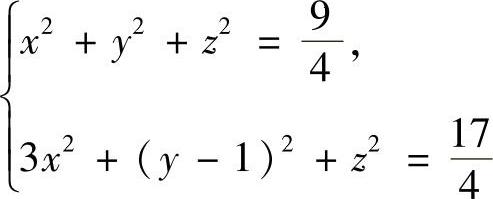
上对应于点x=1的处的切线方程与法平面方程.

解　当x=1时，有

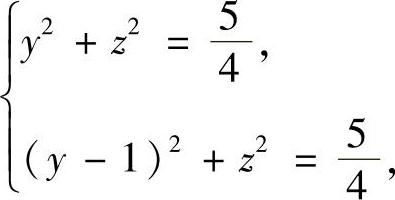
解之得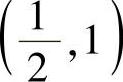与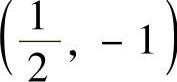.于是对应于x=1的点是，

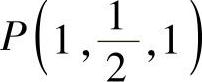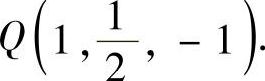
设

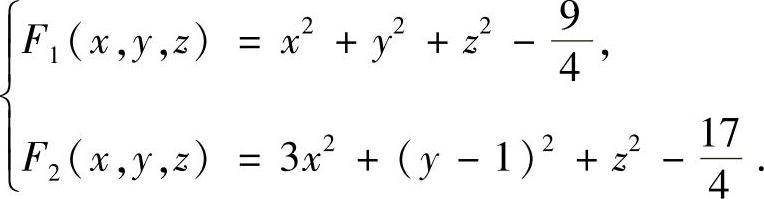
通过计算易知，

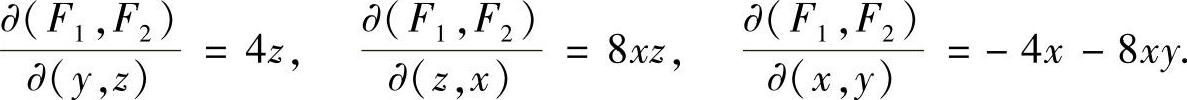
在点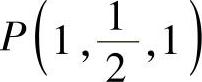，有

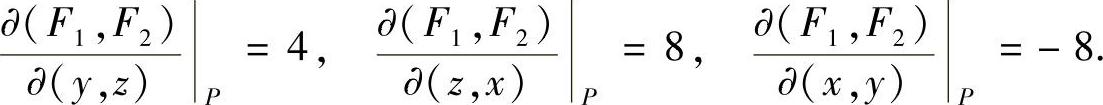
于是，切线方程和法平面方程分别为：

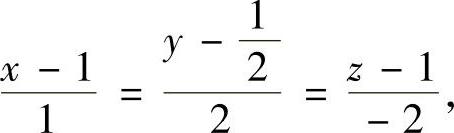
和

x+2y-2z=0；

在点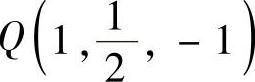，有

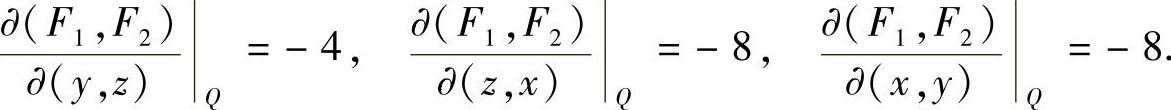
于是，切线方程和法平面方程分别为：

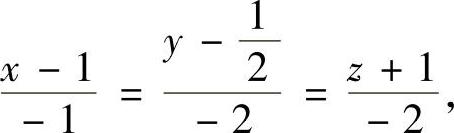
和

x+2y+2z=0.

例6.39 选择题：设函数f（x，y）在点（0，0）附近有定义，且f_x（0，0）=3，f_y∣_（0，0）=1，则（ ）（数学Ⅰ）.

（A）dz（0，0）=3dx+dy；

（B）曲面z=f（x，y）在点（0，0，f（0，0））的法向量为（3，1，1）；

（C）曲线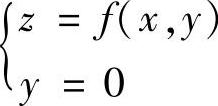在点（0，0，f（0，0））的切向量为（1，0，3）；

（D）曲线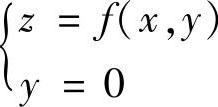在点（0，0，f（0，0））的切向量为（3，0，1）.

解　题目中只假设f（x，y）在点（0，0）有两个偏导数存在，而偏导数存在不能保证f（x，y）在点（0，0）可微，所以（A）不能选.

令F（x，y，z）=f（x，y）-z，易知，曲面z=f（x，y）在点（0，0，f（0，0））的法向量为±（3，1，-1）.因此（B）不能选.

曲线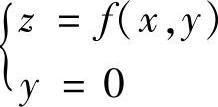的参数方程为：

x=x，y=0，z=f（x，0）.

因此曲线在点（0，0，f（0，0））的切向量为（1，0，3），故选（C）.

例6.40 给定曲面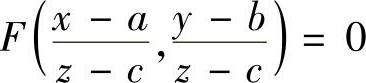（a，b，c为常数），或由它确定的曲面z=z（x，y）.证明：

（1）曲面的切平面通过一定点；

（2）函数z=z（x，y）满足方程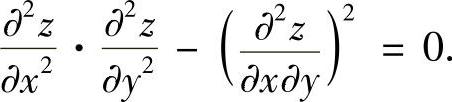

证明 （1）由

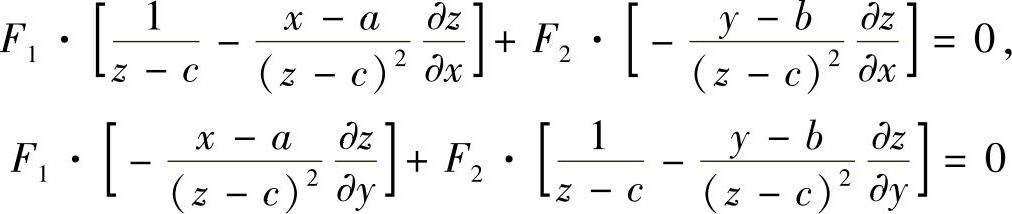
及F₁，F₂不能同时为零，可得

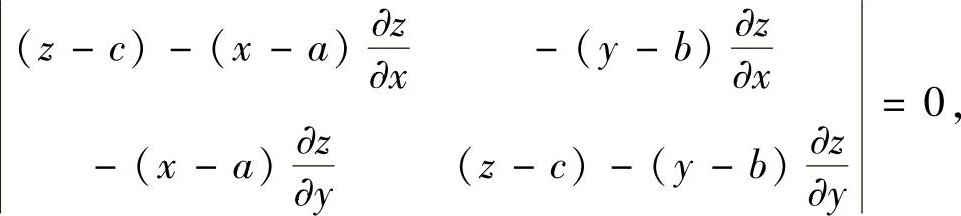
化简得

由此可以看出，曲面z=z（x，y）的切平面过定点（a，b，c）.

（2）对上式两边再分别关于x，y求偏导，得

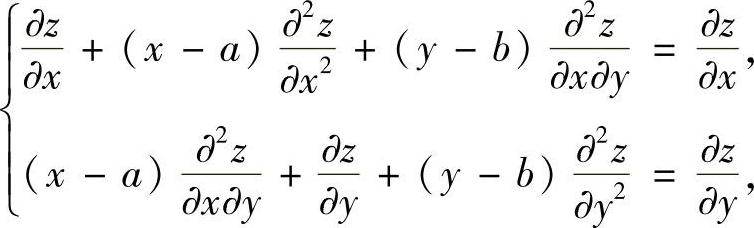
即

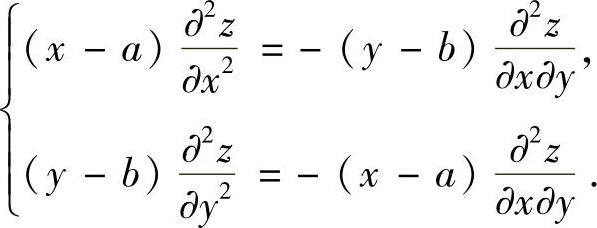
由此可见，当（x-a）（y-b）≠0时，等式成立.由函数连续可微知，对x=a或y=b时等式仍成立.

类题 证明：可微曲面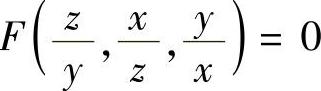的切平面过一定点.

例6.41 设

求f（x，y）在点（0，0）的四阶泰勒多项式，并求出

（北师大）.

解 由于

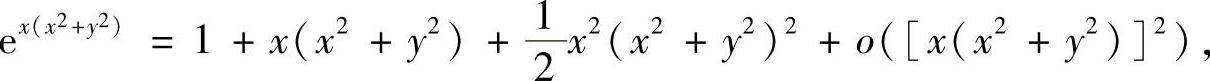
所以

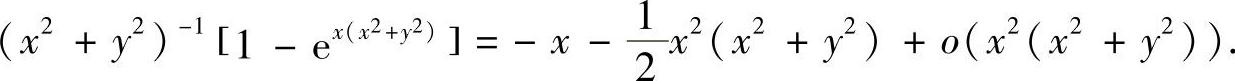
由泰勒展开式的唯一性知，f（x，y）在点（0，0）的四阶泰勒展开式为：

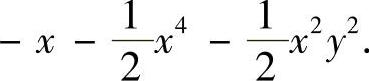
由此可得

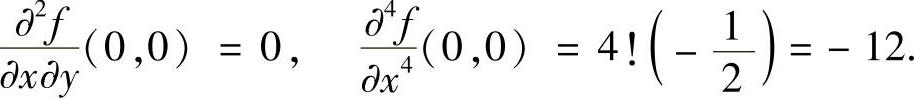
例6.42 设f（x，y）在单位圆域D：x²+y²≤1上具有一阶连续的偏导数，且满足∣f（x，y）∣≤1.证明：在单位圆内有一点（x₀，y₀），使得

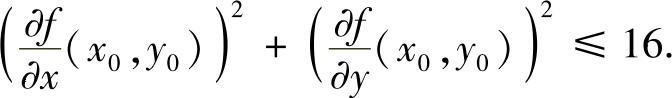
证明 设g（x，y）=f（x，y）+2（x²+y²），则在单位圆周x²+y²=1上显然有g（x，y）≥1.而g（0，0）≤1，所以或者g在D上恒等于1，或者在单位圆内存在一点（x₀，y₀），使g在该点取到极小值.总之，必在单位圆内存在一点（x₀，y₀），使得

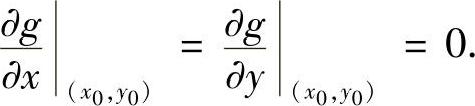
由此可得

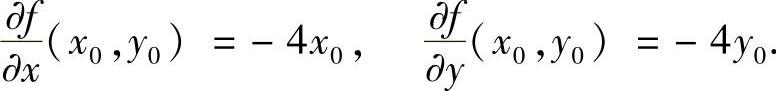
故

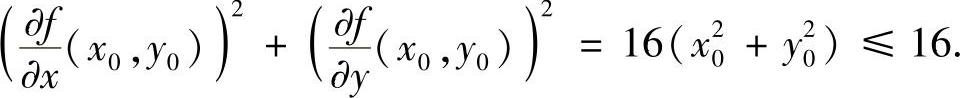
例6.43 证明：函数

f（x，y）=（1+e^y）cosx-ye^y

有无穷多个极大值，但无极小值（大连海运学院）.

证明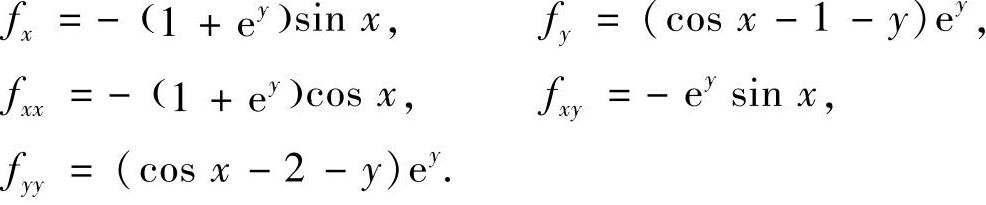

令f_x=0，f_y=0，解方程组可得无穷多个驻点（nπ，cosnπ-1）（n=0，±1，±2，…）.

当n为偶数时，驻点为（2kπ，0）（k=0，±1，±2，…），此时

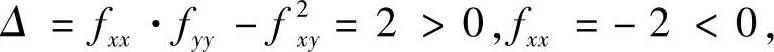
故f（x，y）在驻点（2kπ，0）处取得极大值，极大值为f（2kπ，0）=2.

当n为奇数时，驻点为（（2k+1）π，-2），此时

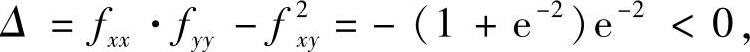
f（x，y）在（（2k+1）π，-2）处无极值.综上知，f（x，y）有无穷多个极大值，但无极小值.

注6.8 在一元函数中，极大值与极小值总是交替出现，但在多元函数中这种情况却不一定发生.例6.43正说明了这一点.

例6.44 设D是由光滑封闭曲线L所围成的区域，f（x，y）在有二阶连续偏导数，且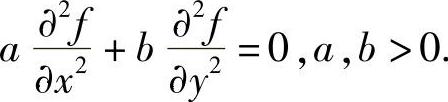如果f在L上等于常数C，证明：f在D上恒等于常数C.

证明 只需证明：f的最值不可能在D内取到即可.若∃（x₀，y₀）∈D，使得f在（x₀，y₀）点达到它在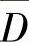上的最大值或最小值.由f的连续性可知，（x₀，y₀）必是f的极大值点或极小值点，因而应有f_x（x₀，y₀）=0，f_y（x₀，y₀）=0.由已知条件，易知判别式

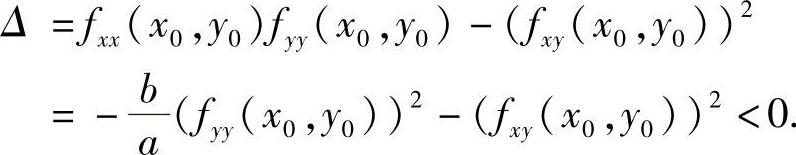
由此可知，（x₀，y₀）不是f的极值点.这与上面的假设矛盾，因而f在D上的最值只能在边界L上取到，所以f在D上恒等于常数C.

例6.45 求f（x，y）=x²-xy+y²-2x+y在全平面上的最大最小值.

解法1 令f_x=2x-y-2=0，f_y=-x+2y+1=0可得驻点（1，0）.通过计算易知，Δ=f_xx·f_yy-（f_xy）2=3>0，f_xx=2>0，所以（1，0）为极小点，极小值为f（1，0）=-1.注意到

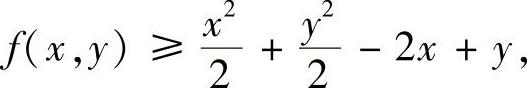
于是有

由此可见，f（x，y）在全平面上无最大值.而另一方面，∃M>0，当x≥M或y≥M时

f（x，y）>f（1，0）=-1.

即f（x，y）在有界闭域：x≤M，y≤M上的最小值-1，必是f（x，y）在全平面上的最小值.

解法2　先固定x，求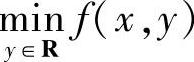.将f（x，y）改写为：

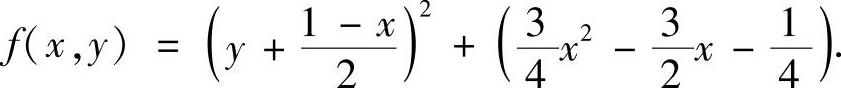
显然，

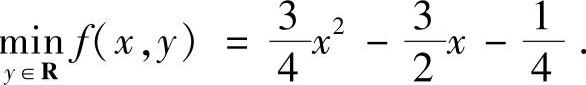
于是

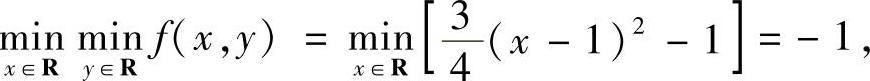
故

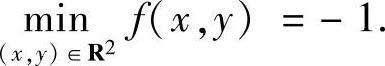
又由f（0，y）=y²+y可知，f（x，y）在R²上无最大值.

解法3　用配方法.

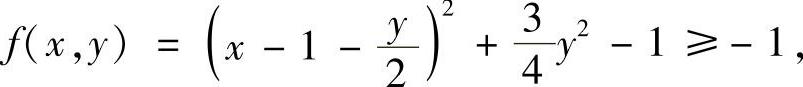
且f（1，0）=-1即最小值为-1，但无最大值.

例6.46　对三角形ABC，求3sinA+4sinB+18sinC的最大值.

解　这个题目有一定难度，在此我们将采用累次求最值的方法求其最大值.

三角形三个角A，B，C的取值范围为

（A，B，C）∈D≜{（α，β，γ）|α+β+γ=π，α>0，β>0，γ>0}.

首先，求3sinA+4sinB+18sinC在D的闭包

E={（α，β，γ）|α+β+γ=π，α≥0，β≥0，γ≥0}

上的最大值，此时有

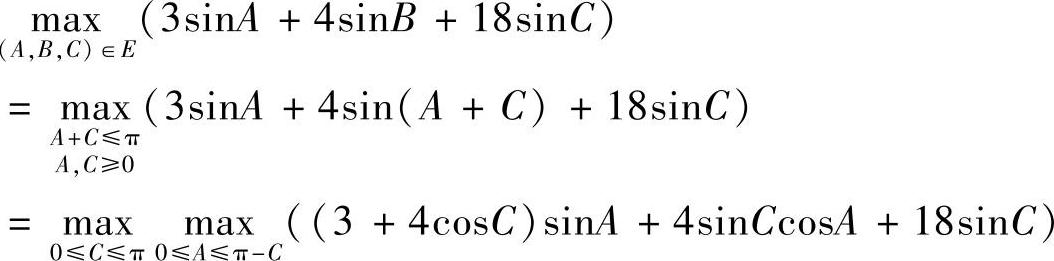
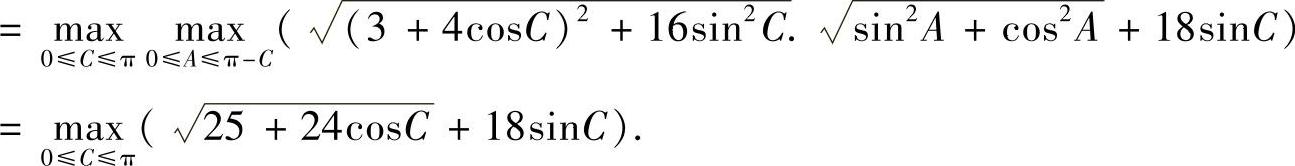
记

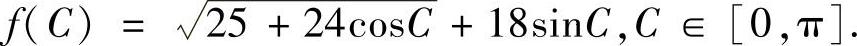
由于

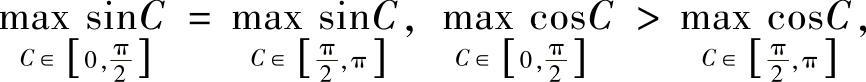
所以　f（C）在[0，π]上的最大值实际上在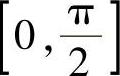上取到.因此，只须考虑f（C）在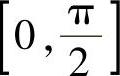上的最大值即可.

令

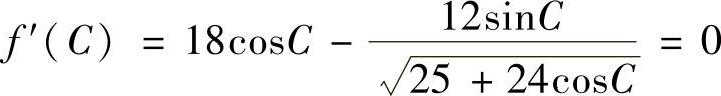
可得

（8cosC-1）（27cos²C+32cosC+4）=0.

解之可得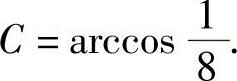于是

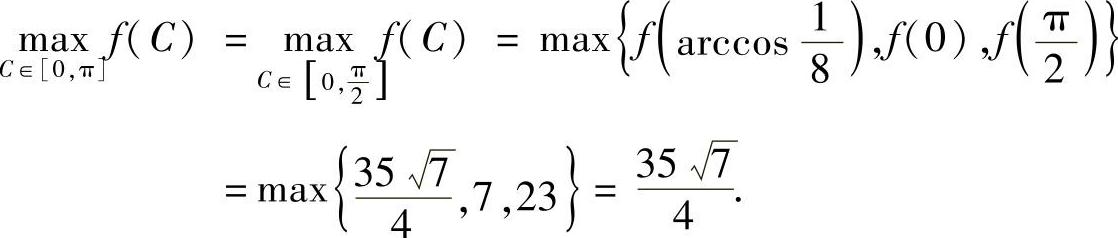
下面求3sinA+4sinB+18sinC在E的边界上（A，B，C之一为零）的最大值.

若A=0，则B+C=π，此时目标函数变成4sinB+18sinC=22sinB，易见最大值为22；

若B=0，则A+C=π，此时目标函数变成3sinA+18sinC=21sinA，易见最大值为21；

若C=0，则A+B=π，此时目标函数变成3sinA+4sinB=7sinA，易见最大值为7.综上可知，所求的最大值为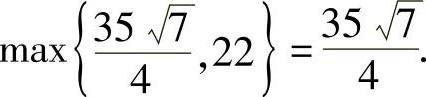

类题　已知x，y，z为实数，且e^x+y²+z=3，证明：

e^xy²z≤1.

提示　记a=e^x，b=y²，c=z，则a，b，c是三个非负实数，所求问题转化为计算二元函数u（a，b）=ab（3-a-b）在有界闭区域D={（a，b）|a+b≤3，a≥0，b≥0}上的最大值.

例6.47 证明：

f（x，y）=yx^y（1-x）<e^-1，0<x<1，0<y<+∞.（吉林大学）.

证明 只要证明f（x，y）在区域0<x<1，0<y<+∞上的最大值小于e^-1即可.

显然，f（x，y）在区域0<x<1，0<y<+∞的边界上恒为0，而在区域内部f（x，y）>0.由于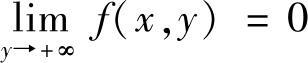，因此，它的最大值只能在区域内部达到.(www.xing528.com)

令

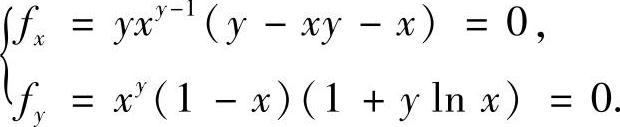
注意到0<x<1，y>0，上述方程组可化为：

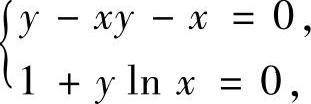
即

y（1-x）=x，x^y=e^-1.

在这样的点上，f（x，y）=yx^y（1-x）=xe^-1<e^-1，即f（x，y）在区域0<x<1，0<y<+∞上的最大值小于e^-1.

类题 证明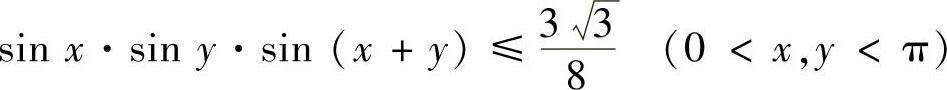（中科院）.

例6.48 证明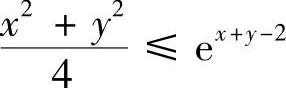：对x≥0，y≥0成立.

证明 将原不等式变形为

（x²+y²）e^-x-y≤4e^-2，∀x≥0，y≥0.

这样就将问题转化为求f（x，y）=（x²+y²）e^-x-y在区域D={（x，y）x≥0，y≥0}上的最大值.

令

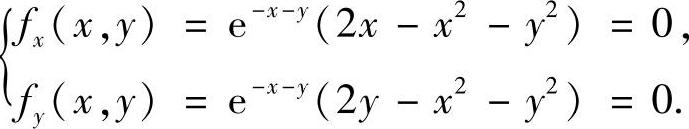
解之可得，在D的内部有唯一驻点（1，1），且f（1，1）=2e-2.

注意到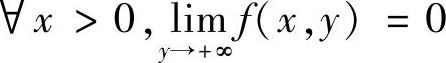，和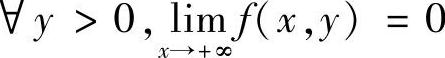，所以f（x，y）在D的内部最大值为f（1，1）=2e^-2.

下面求f（x，y）在D的边界上的最大值.

在y=0上，f（x，0）=x²e^-x，x≥0.

令f_x（x，0）=0，可得驻点x=0，2.此时f（0，0）=0，f（2，0）=4e^-2.因此，f（x，y）在y=0上的最大值为4e^-2.

同理，f（x，y）在x=0上的最大值为4e^-2.综上，f（x，y）在D上的最大值为4e^-2，即（x²+y²）e^-x-y≤4e^-2，∀x≥0，y≥0.

例6.49　试求函数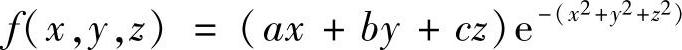的最大最小值，其中a²+b²+c²>0.

解　令f_x=0，f_y=0，f_z=0可得

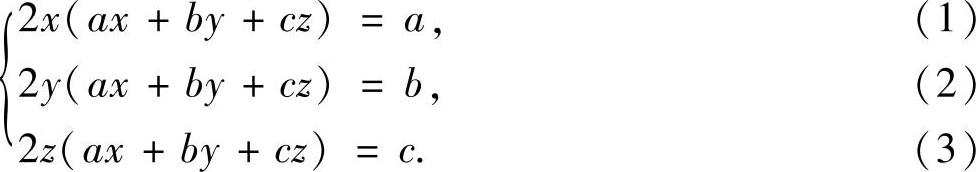
（1）×a+（2）×b+（3）×c可得

2（ax+by+cz）²=a²+b²+c²，

即

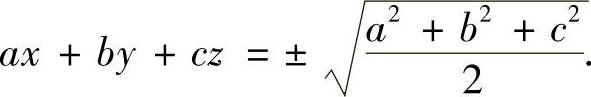
记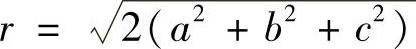，由式（1）、式（2）、式（3）可得两个驻点：

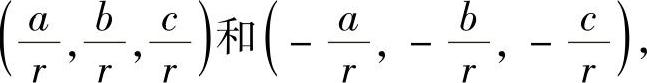
函数f（x，y，z）在这两个驻点处的值分别为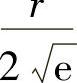和.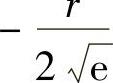

下面我们将说明这两个值就是f在R³上的最大值和最小值.

考虑以原点为中心，ρ为半径的球面Sρ：x=ρcosα，y=ρcosβ，z=ρcosγ.在Sρ上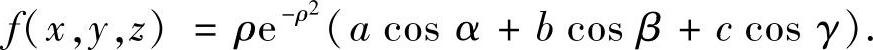，所以

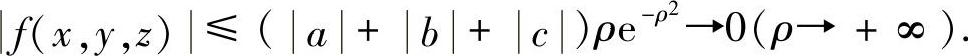
从而存在ρ₀>0，使当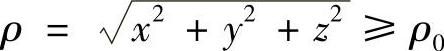时，有

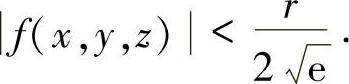
由此可见，f在整个R³上的最值与它在有界闭域D={（x，y，z）ρ≤ρ₀}上的最值相同.由上式知，f在D上的最值一定在D的内部达到，因而必在驻点处达到，故f在整个R³上的最大、最小值分别为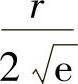和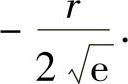

例6.50　求f（x，y，z）=xyz在条件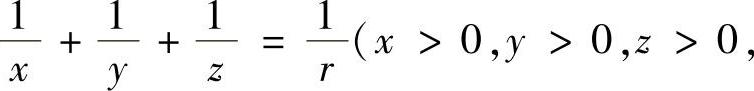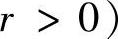下的极小值；并证明不等式

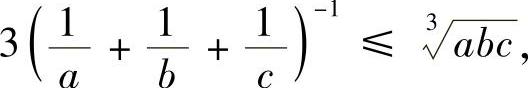
其中a，b，c为任意正实数.

解　构造拉格朗日函数

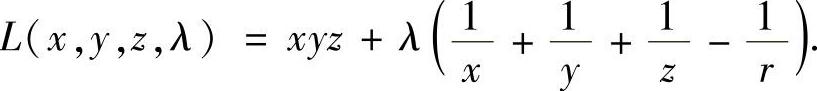
令

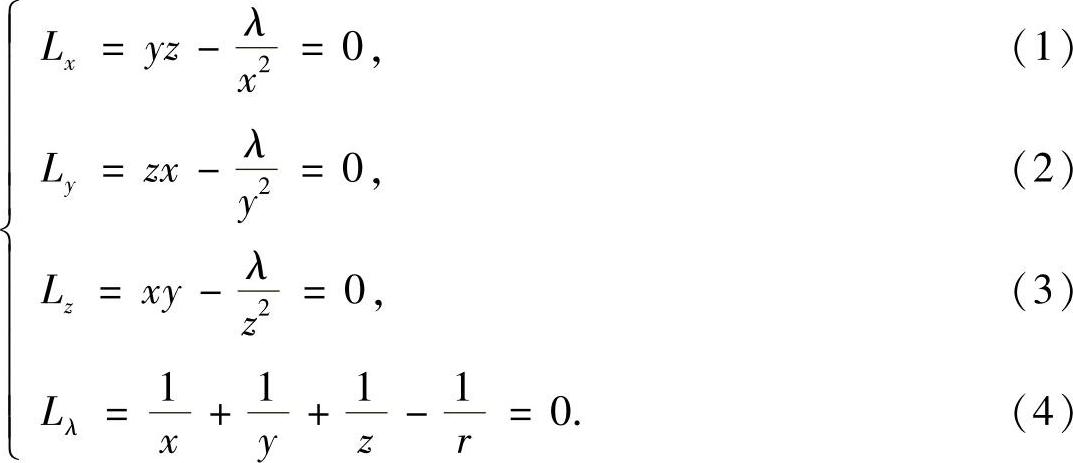
由式（1）、式（2）、式（3）易得

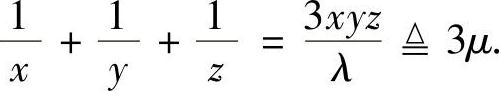
将它们代入式（4）求出，从而解出驻点为x=y=z=3r，λ=（3r）4.

下面来判断这个驻点是极小值点.

由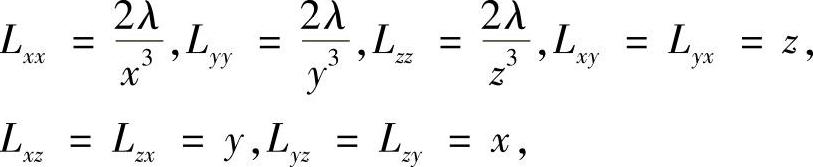

可得L在驻点P₀处的海色阵

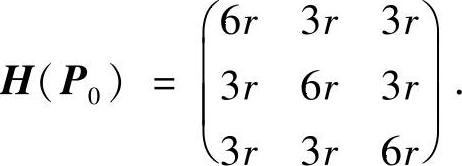
因为

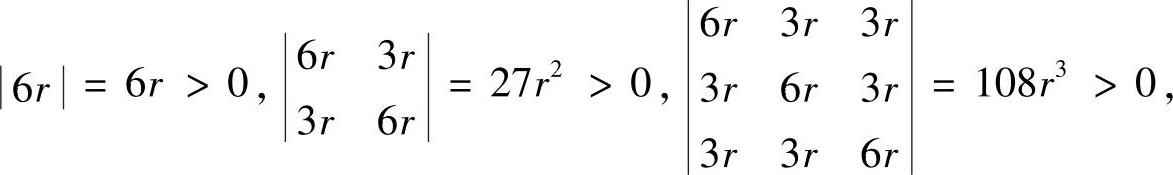
所以H（P₀）正定，故驻点为极小值点，而且极小值为f（3r，3r，3r）=（3r）3.

注意到在x>0，y>0，z>0上，变量x，y，z中任何一个趋向于+∞，都将有f➝+∞，所以f在第一卦限的最小值必在有界区域D={（x，y，z）ρ≤ρ₀，x，y，z>0}（其中ρ₀>0是一个适当的正常数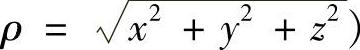，上取到.而由约束条件知，x，y，z中均不可能趋向于0，因此f在第一卦限的最小值必在D的内部取到.由于f在D的内部有唯一的极小值点，所以这个极小值点也是最小值点，且最小值为（3r）3.这样，

当x>0，y>0，z>0且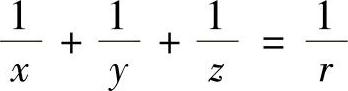时，有xyz≥（3r）3.（5）

令x=a，y=b，z=c，则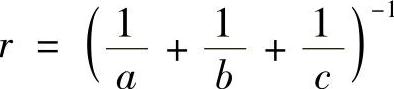，代入不等式（5），有

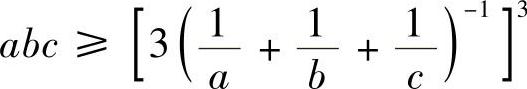
或

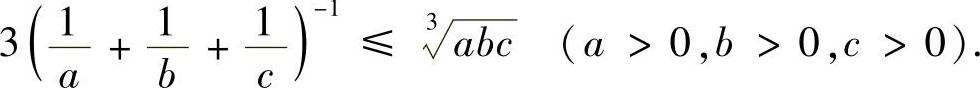
例6.51　求x>0，y>0，z>0时，函数

f（x，y，z）=lnx+2lny+3lnz

在球面x²+y²+z²=6r²上的极大值；并证明当a，b，c为正实数时，有

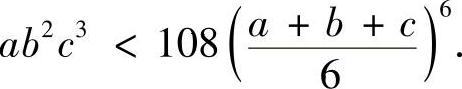
（清华大学）.

解　构造拉格朗日函数

L（x，y，z，r）=lnx+2lny+3lnz+λ（x²+y²+z²-6r²）.

令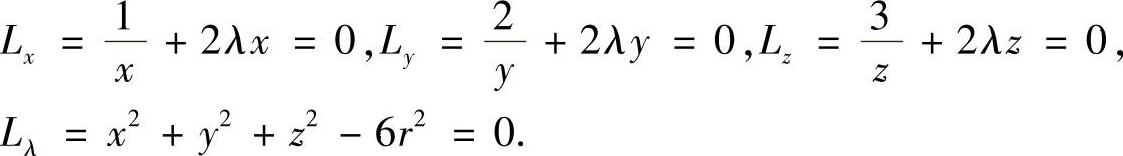

解出驻点为x=r，，，.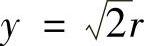

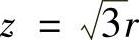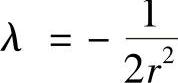下面来判断这个驻点为极大值点.

由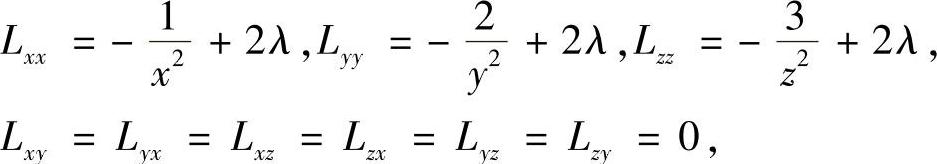

可得L在驻点P₀处的海色阵

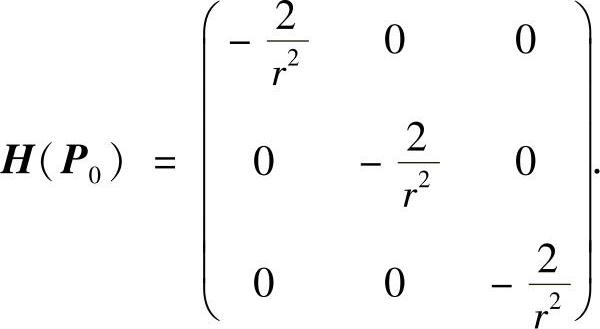
显然H（P₀）负定，故驻点为极大值点，而且极大值为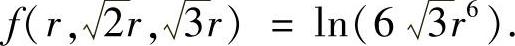

因为f在球面x²+y²+z²=6r²位于第一卦限的部分上连续，所以f必在其上取到最大值.注意到当动点趋向于边界线（其上x，y，z之一为0）时，f➝-∞，故f的最大值只能在内部取到，而内部有唯一的极大值点，因此这个极大值点也必是最大值点，且最大值为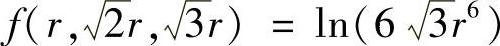，即

当x>0，y>0，z>0且满足x²+y²+z²=6r²时，有

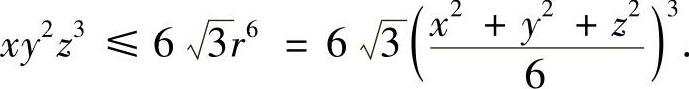
取x²=a，y²=b，z²=c，上式变为：

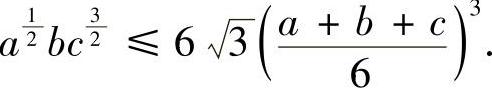
两边平方，即得

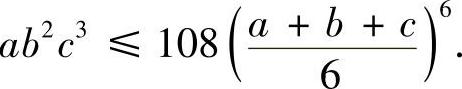
例6.52　设有一座小山，取它的底面所在的平面为xOy坐标平面，其底部所占的区域为D={（x，y）x²+y²-xy≤75}.小山的高度函数为

h（x，y）=75-x²-y²+xy.

（1）设M（x₀，y₀）为区域D上一点，问h（x，y）在该点沿平面上什么方向的方向导数最大？若记此方向导数的最大值为g（x₀，y₀），试写出g（x₀，y₀）的表达式；

（2）现欲利用此小山开展攀岩活动，为此需要在山脚寻找一上山坡度最大的点作为攀登的起点.也就是说，要在D的边界线x²+y²-xy=75上找出使（1）中的g（x，y）达到最大值的点.试确定攀登起点的位置（数学Ⅰ）.

解　（1）高度函数h（x，y）在点M（x₀，y₀）处的梯度是

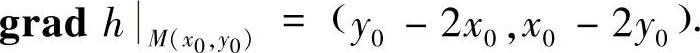
由梯度的几何意义知，沿此梯度方向，高度函数h（x，y）的方向导数取最大值，并且这个最大值就是此梯度的模.于是

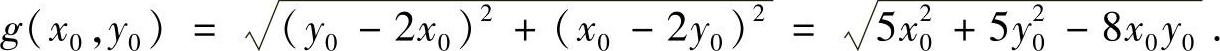
（2）令f（x，y）=g²（x，y）=5x²+5y²-8xy.依题意，只需求函数f（x，y）在约束条件x²+y²-xy=75下的最大值点即可.

令L（x，y，λ）=5x²+5y²-8xy+λ（x²+y²-xy-75），则由

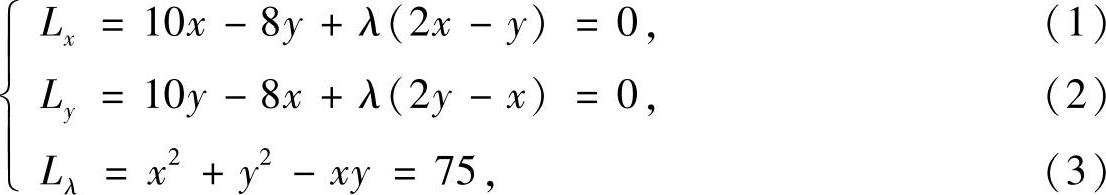
可得

（x+y）（λ+2）=0，即x+y=0或λ=-2.

当x+y=0时，由式（3）可得：x=±5，y=∓5；

当λ=-2时，由式（1）得：y=x.再由式（3）可得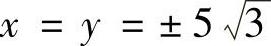：.这样就得到了四个驻点：

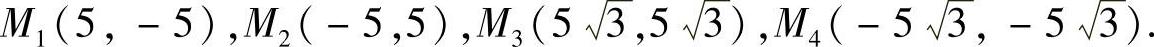
计算可知，

f（M₁）=f（M₂）=450，f（M₃）=f（M₄）=150，故M₁，M₂点都可作为攀登的起点.

例6.53　求函数f（x，y）=ax²+2bxy+cy²在闭区域D={（x，y）x²+y²≤1}上的最大值与最小值.这里b²-ac<0，a，b，c>0.

解　先考虑D的内部intD={（x，y）x²+y²<1}，这是无条件极值问题.

令

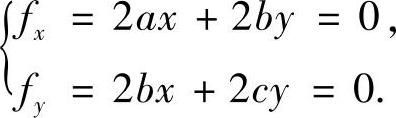
由b²-ac<0知，方程组的系数行列式不等于零，因此方程组只有零解x=0，y=0，即（0，0）点是驻点.通过计算易知，在（0，0）点

A=f_xx=2a，B=f_xy=2b，C=f_yy=2c

Δ=AC-B²=4（ac-b²）>0，A>0.

所以（0，0）点是f的极小值点，极小值为f（0，0）=0.

再考虑D的边界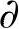D={（x，y）x²+y²=1}，这是条件极值问题.

构造拉格朗日函数

L（x，y，λ）=ax²+2bxy+cy²-λ（x²+y²-1）.

令

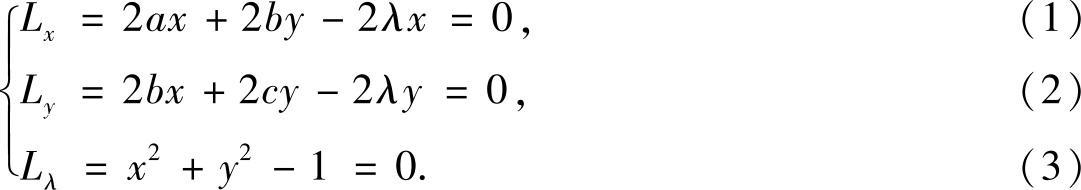
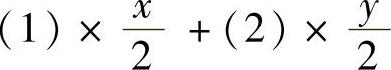，并注意到式（3），可得

f（x，y）=λ（x²+y²）=λ.

下面来求λ的值.

由（3）知，由方程（1）、（2）所构成的方程组有非零解，因此其系数行列式等于零，即

λ²-（a+c）λ+ac-b²=0.

因为Δ=（a+c）2-4（ac-b²）=（a-c）2+4b²>0，所以，关于λ的方程有两个相异实根，即

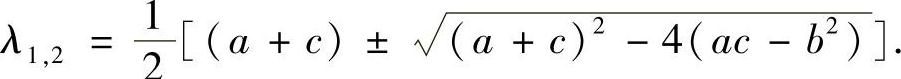
由于连续函数f在有界闭集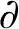D={（x，y）∣x²+y²=1}上必存在最大值和最小值，因此f在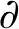D上的最大值为λ₁，最小值为λ₂.将其与D内部的极值f（0，0）作比较，就得到f在D上的最大值为max{λ₁，0}=λ₁，最小值为min{λ₂，0}=0.

类题　求函数f（x，y）=2x²+12xy+y²在区域x²+4y²≤25上的最大值与最小值（复旦大学）.

注6.9　从本例的求解过程可以看出，二元二次型f（x，y）在圆周x²+y²=1的最大值和最小值分别等于该二次型矩阵的最大特征根和最小特征根.对一般情形，这个结论仍然成立，即二次型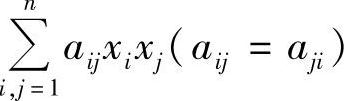在n维单位球面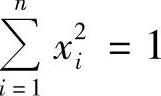上的最大值和最小值也分别等于该二次型矩阵A=（a_ij）_n×n的最大特征根和最小特征根.

例6.54　椭球面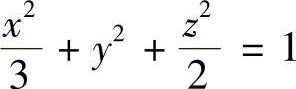被过原点的平面2x+y+z=0截成一个椭圆，求此椭圆的面积.

解　只要求出椭圆的长、短半轴即可.设（x，y，z）是椭圆面上任一点，它到原点的距离为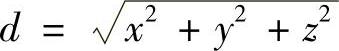，这样问题就转化为求d²在约束条件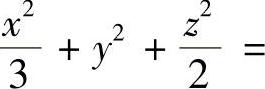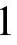和2x+y+z=0下的最值问题.

构造拉格朗日函数

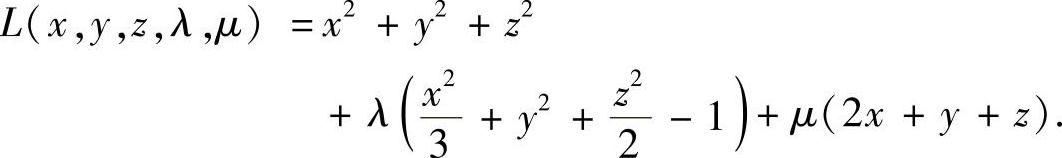
令

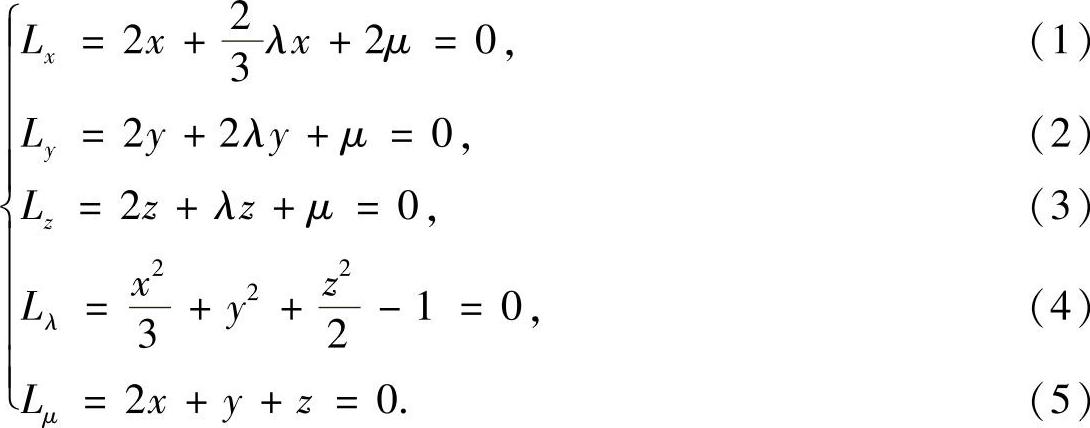
在式（1）、式（2）、式（3）两边分别乘以x，y，z相加，并利用式（4）、式（5）可得

λ=-d².

将上式代入式（1）可得

（d²_-3）x=3_μ.

若d²=3，则μ=0.代入式（2）、式（3）两式可得：y=z=0，再由式（5）可得：x=0.这显然不满足式（4），所以d²-3≠0，于是

同理，将λ=-d²分别代入式（2）、式（3）可得

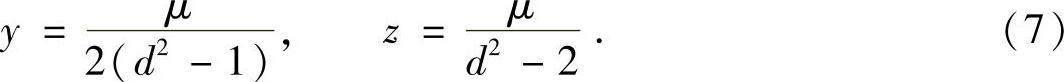
将式（6）、式（7）代入式（5）可得

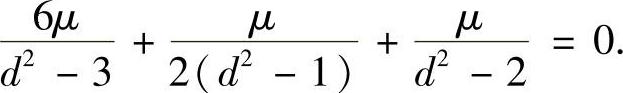
消去_μ（因为μ≠0），整理可得

15（d²）²-49d²+36=0.（8）

因为函数d²=x²+y²+z²在有界闭集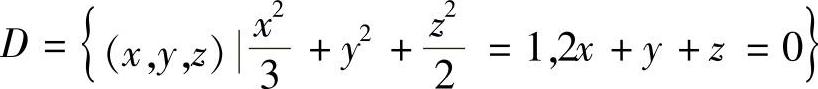上连续，所以d²在D上一定存在最大值和最小值，且它们分别是方程（8）的大根和小根，即它们分别是椭圆的长、短半轴的平方.由韦达（Viète）定理，有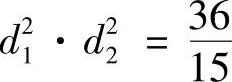

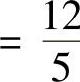
2

，于是椭圆的面积为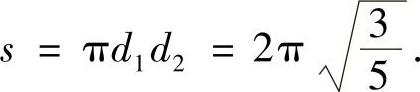

例6.55　求a，b之值，使得椭圆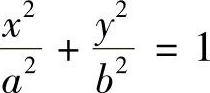包含圆（x-1）2+y²=1，且面积最小.

解　椭圆的面积S=πab.先求a，b所满足的约束条件φ（a，b）=0.

欲使S最小，必须要求椭圆与圆相切，在切点处纵坐标y值和斜率y′值应相等，即

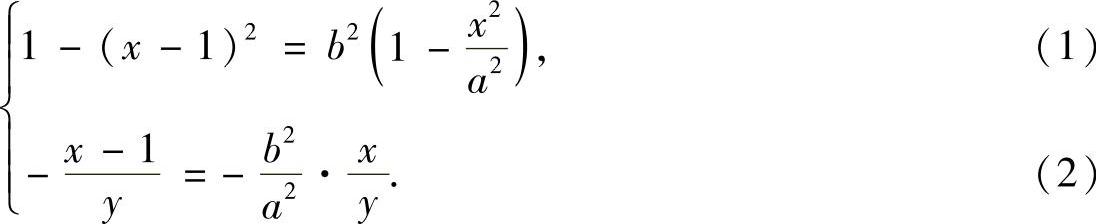
从式（2）中解出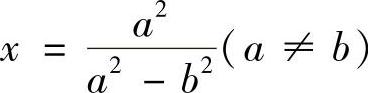，代入式（1）可得：

φ（a，b）=a²-a²b²+b⁴=0.

构造拉格朗日函数

L（a，b，λ）=πab-λ（a²-a²b²+b⁴）.

由

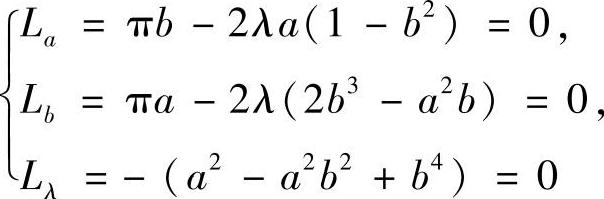
解之可得：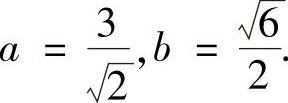

由于实际问题存在最小值，所以这唯一的极值点必是最小值点，最小值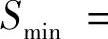

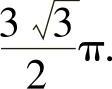
例6.56 求由方程

x²+2y²+3z²-2xy-2yz-2=0

所确定的隐函数z=z（x，y）的极值.

解法1 直接法.对方程两边分别关于x，y求偏导：

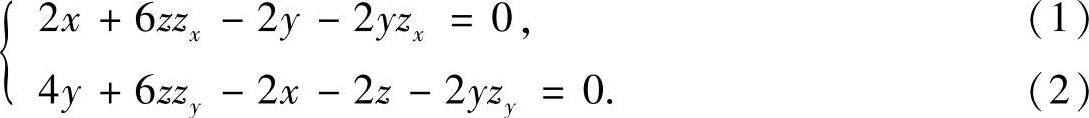
令z_x=z_y=0，可得

x=y， 2y-x-z=0.

由此得y=x，z=x.代入原方程可得：x=±1，即有两个驻点（1，1，1）和（-1，-1，-1）.

在式（1）、式（2）两边再求偏导可得

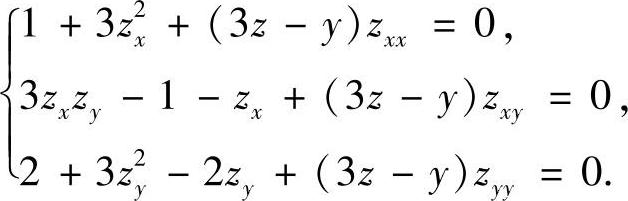
在驻点（1，1，1）处算得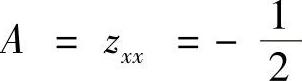：，B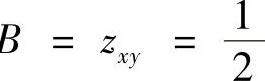，C=z_yy=-1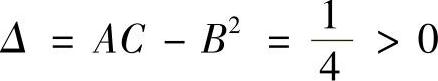，，所以驻点（1，1，1）为极大值点，极大值为z=1.

在驻点（-1，-1，-1）处算得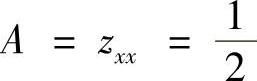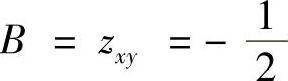：，，C=z_yy=1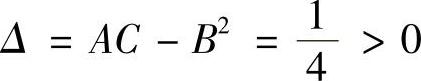，，所以驻点（-1，-1，-1）为极小值点，极小值点为z=-1.

解法2　间接法.取目标函数为f（x，y，z）=z，约束条件为x²+2y²+3z²-2xy-2yz-2=0.构造拉格朗日函数：

L（x，y，z，λ）=z+λ（x²+2y²+3z²-2xy-2yz-2）.

令

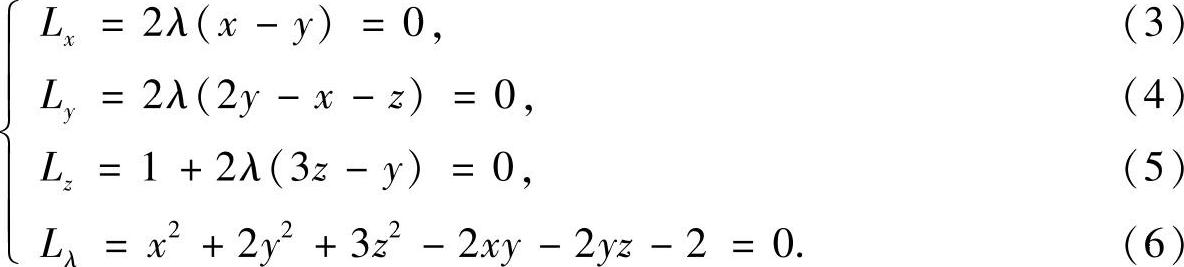
由式（5）可见，λ≠0.于是可解出x=y=z=±1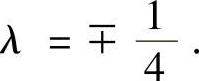，下面来判断驻点是否为极值点.

L_xx=2λ，L_yy=4λ，L_zz=6λ，L_xy=L_yx=-2λ，

L_xz=L_zx=0，L_yz=L_zy=-2λ.

在驻点（1，1，1）处，相应地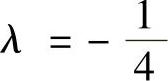，海色阵为

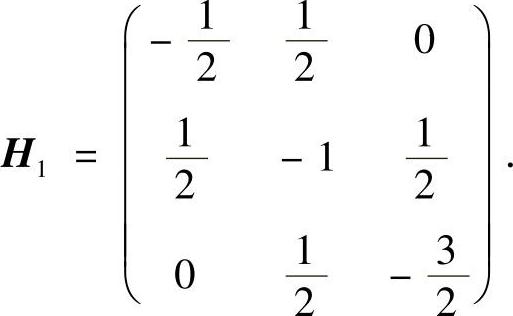
它的主对角线行列式为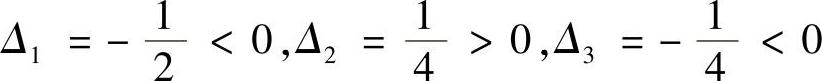：，所以H₁负定，故驻点（1，1，1）为极大值点，极大值为z=1.

在驻点（-1，-1，-1）处，相应地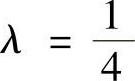，海色阵为

它的主对角线行列式为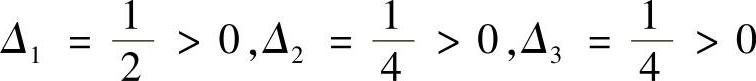：，所以H₂正定，故驻点（-1，-1，-1）为极小值点，极小值为z=-1.

例6.57　设三角形的三个顶点分别位于曲线f（x，y）=0，φ（x，y）=0，ψ（x，y）=0上.求证：若三角形的面积达到极值，则曲线在三角形顶点处的法线都通过该三角形的垂心（华中工学院）.

证明　如图6-6所示：

若三角形面积达到极值，即函数

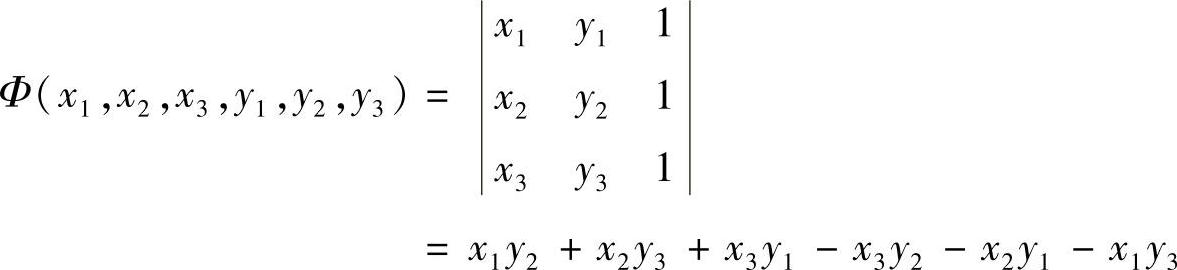
在条件f（x₁，y₁）=0，ψ（x₂，y₂）=0，φ（x₃，y₃）=0下达到极值.

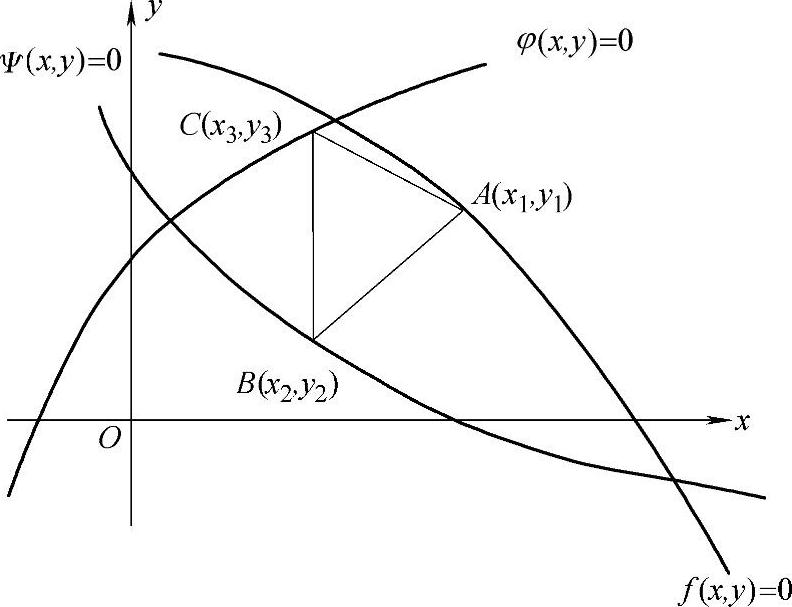
图6-6　例6.56图

构造拉格朗日函数

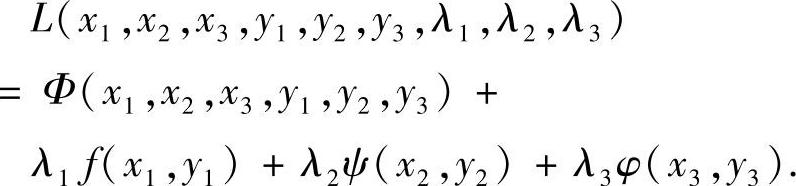
由取得极值的必要条件可知：

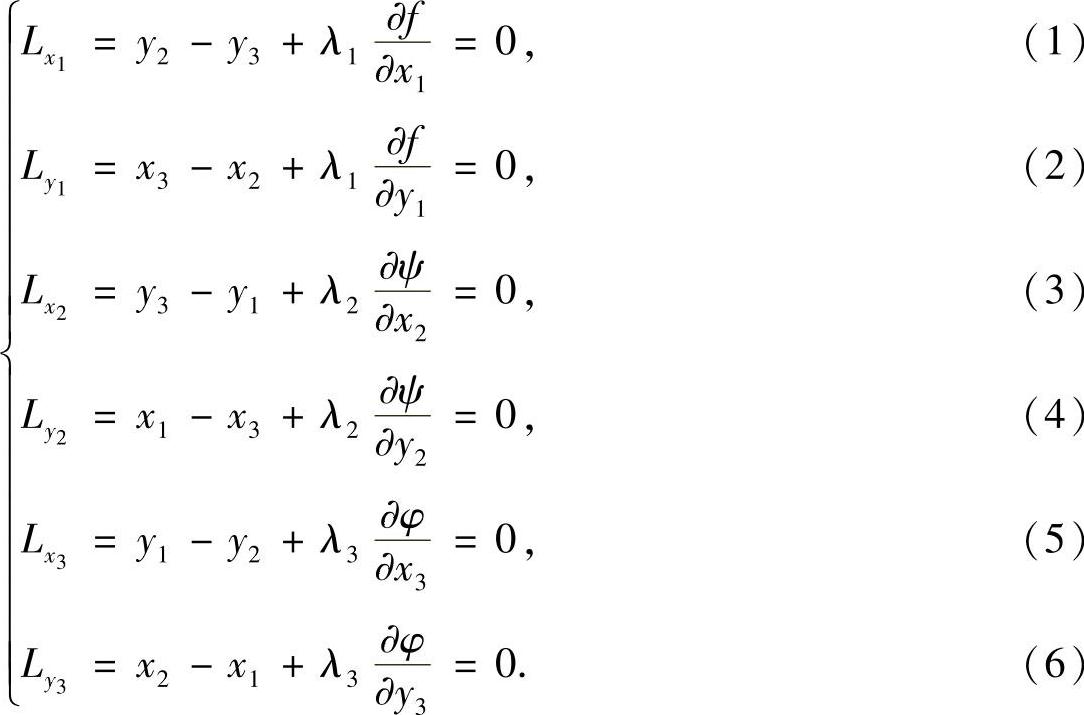
若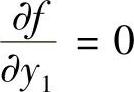，由式（2）知，x₂=x₃.由此知，△ABC的BC边与x轴垂直，且曲线f（x，y）=0上在点A处的切线平行于y轴，所以点A处曲线的法线与BC垂直，即点A处的法线过△ABC的垂心；

若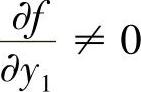，则曲线f（x，y）=0上点A处的切线斜率为

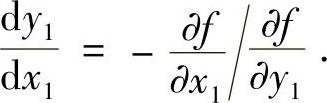
而BC边的斜率为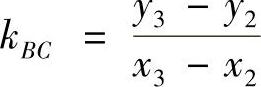.由式（1）、式（2）易知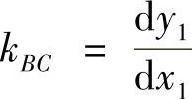，，即曲线f（x，y）=0在点A处的切线平行于BC，从而点A处的法线过△ABC的垂心.

同理可证：点B，C处的法线也经过△ABC的垂心.