考研数学分析总复习：全微分及其定义

设P₀（x₀，y₀）∈D⊂R²，给自变量x和y增量Δx，Δy，相应地可得到函数值的增量Δz.当ρ➝0时，若Δz可表示为如下形式：

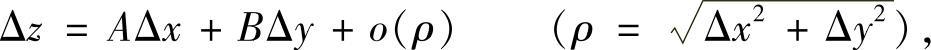
其中，A，B是与Δx，Δy无关而与x₀，y₀有关的常数，则称f在点P₀可微，并把其线性主部AΔx+BΔy称为f在点P₀的全微分，记为dz∣_P0或df（x₀，y₀）.习惯上写成：dz∣_P0=A∣P₀^dx+B∣_P0dy.

从定义可以看出，如果函数f在点P₀可微，则在P₀附近有

f（x₀+Δx，y₀+Δy）≈f（x₀，y₀）+AΔx+BΔy.

因此可微的意义在于在点P₀附近f可用一个Δx和Δy的线性函数来逼近.

全微分的性质：

（1）若f在点（x₀，y₀）可微，则A=f_x（x₀，y₀），B=f_y（x₀，y₀）.这样，全微分公式可以写成：df∣_P0=f_x（x₀，y₀）dx+f_y（x₀，y₀）dy.若不特指某一点，则可写成：

df=f_x（x，y）dx+f_y（x，y）dy；

（2）若f在点（x₀，y₀）可微，则f在点（x₀，y₀）连续；

（3）若f在点（x₀，y₀）可微，则对∀l=（cosα，sinα），f在点（x₀，y₀）沿l的方向导数存在，且

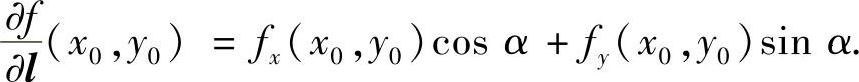(www.xing528.com)

另外，多元函数的微分也具有一阶形式的不变性，利用这个性质可求函数的偏导数.

证明函数f在点（x₀，y₀）不可微常用的方法：1）证明f在点（x₀，y₀）至少有一个偏导数不存在；2）证明f在点（x₀，y₀）不连续；3）从定义出发，证明

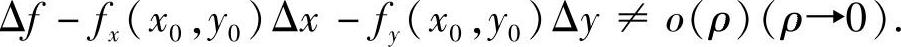
多元函数的连续性、可偏导性以及可微性之间的关系如图6-1所示.由此可见，仅由偏导数存在是推不出连续的，这一点与一元函数有着本质的区别.由连续性也推不出偏导数存在，考虑函数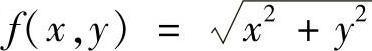在点（0，0）.

方向导数与连续性之间也不存在蕴含关系.例如

在点（0，0）沿任何方向的方向导数都存在且为0，但该函数在点（0，0）无极限，当然也不连续.又如，

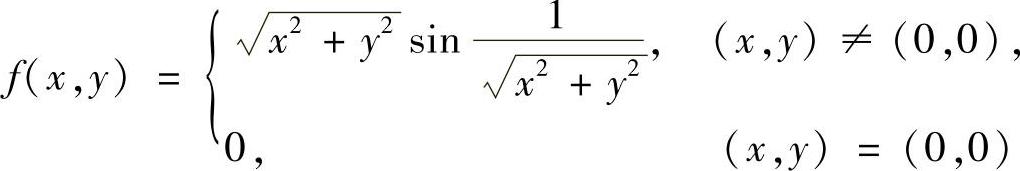
在原点连续，但它沿任何方向的方向导数都不存在.

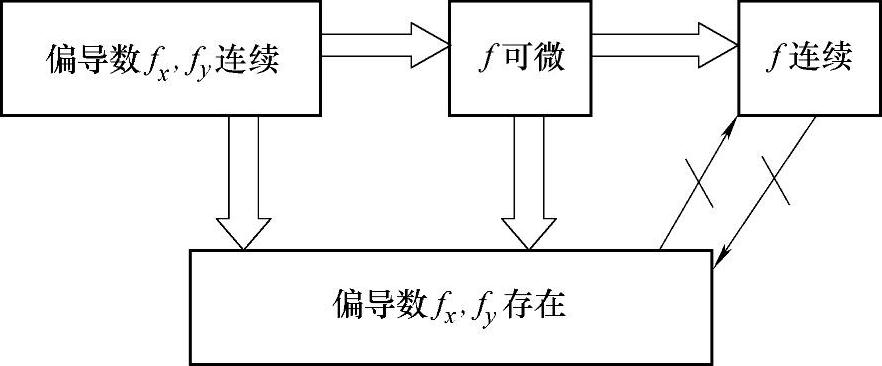
图6-1　多元函数的连续性、可偏导性以及可微性之间的关系