欧氏空间基本定理：考研数学分析真题精选

R中的六个基本定理除了“确界原理”“单调有界定理”由于涉及点之间的大小关系而不再有意义外，其余的定理在Rⁿ（n>1）中依然成立.它们是：

（1）闭区域套定理——常用其特殊形式闭矩形套定理；

（2）聚点定理：Rⁿ中的有界无限点集必有聚点；

（3）柯西收敛准则：收敛点列⇔基本列；

（4）紧性定理：Rⁿ中的点集S是紧集⇔S是有界闭集.

例6.1 设S是Rⁿ的子集，则以下三个命题等价：

（1）S是有界闭集；

（2）S是紧集；

（3）S的任一无限子集在S中必有聚点.

证明 由紧性定理可知，（1）⇔（2）.

下证：（1）⇔（3）.

（1）⇒（3）.设S是有界闭集.由聚点定理知，S的无限点集必有聚点，因为S是闭的，所以这个聚点必属于S.

（3）⇒（1）.若S的任一无限子集在S中都有聚点，则显然S中的任一收敛点列{x_k}的极限必属于S，因此S含有它的全部聚点，即S是闭集.

若此时S不是有界的，那么在S中存在点列{x_k}满足(https://www.xing528.com)

∣x_k∣>k， k=1，2，….

而{x_k}是无限集，且在Rⁿ中（因而在S中）没有聚点，矛盾.这表明S是有界集.

例6.2 设S₁，S₂都是Rⁿ中的有界闭集，S₁∩S₂=，证明：存在两个开集O₁和O₂，使得S_i⊂O_i，且O₁∩O₂=.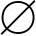

证明 先证：d=d（S₁，S₂）>0.

用反证法.若d=d（S₁，S₂）=0，则由距离的定义知，∃x_n∈S₁，y_n∈S₂，使得

由S₁，S₂的有界性，利用聚点定理知{x_n}，{y_n}都存在收敛子列，仍记为{x_n}，{y_n}，并设x_n➝x，y_n➝y（n➝∞）.由S₁，S₂的闭性知，x∈S₁，y∈S₂.在式（1）中令n➝∞可得x=y，这与S₁∩S₂=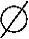矛盾.

定义

则O_i为开集，且S_i⊂O_i，并有O₁∩O₂=.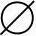

例6.3　设S⊂R²，P₀（x₀，y₀）为S的内点，P₁（x₁，y₁）为S的外点，证明：直线段P₀P₁至少与S的边界∂S有一个交点（华东师大）.

证明　用闭区域套定理.记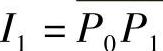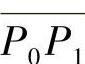（表示直线段P₀P₁，下同），将I₁二等分，分点为P₂.如果P₂是∂S上的点，则问题得证，否则取I₂，使得I₂的两个端点一个是S的内点，而另一个是S的外点.此时，有I₂⊂I₁，且；

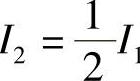再将I₂二等分，分点为P₃.如果P₃是∂S上的点，则问题得证，否则取I₃，使得I₃的两个端点一个是S的内点，而另一个是S的外点.此时，有I₃⊂I₂，且；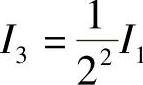

如此下去，要么到某一步时，得到一分点P_n∈∂S，则问题得证；要么这种步骤可无限地进行下去，得到一闭直线段列{I_n}，满足I_n+1⊂I_n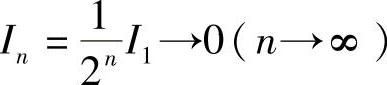，.由闭区域套定理，存在P*属于所有的直线段I_n.

下证：P^*∈∂S.事实上，对∀ε>0，以P*为中心，ε为半径作小圆B_ε（P^*）.由于P*属于所有I_n，而且I_n→0（n→∞），所以当n适当大时，I_n∈B_ε（P^*）.由I_n的造法可知，在B_ε（P^*）既含有S的内点，又含有S的外点，故P*∈∂S.