1)傅里叶系数的渐近性质.
由黎曼引理知,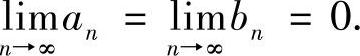
随着f的可导性的提高,an,bn趋向于零的速度也会加快.
命题5.6 设f在[-π,π]上有直到k+1阶的导数,f(k+1)在[-π,π]上可积,且f(l)(π)=f(l)(-π)(l=0,1,…,k),则
2)傅里叶级数的唯一性定理.
命题5.7 设f是以2π为周期的连续函数,且其傅里叶系数均等于0,即a0=0,an=bn=0,n=1,2,…,则f必是恒为零的常值函数.
这个命题告诉我们,如果两个连续函数在某一给定区间上的傅里叶级数相同,则这两个连续函数相等.
3)傅里叶级数的逐项积分定理:设f(x)在[-π,π]上可积,且
则级数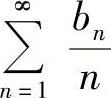 一定收敛,且∀x0,x∈[-π,π],有
一定收敛,且∀x0,x∈[-π,π],有
进而,取x0=0可得
上式右端是上式左端函数的傅里叶级数.
注5.8 只要f可展开成傅里叶级数,不论这个级数是否收敛,是否收敛于f(x),它逐项积分后所得到的级数一定收敛于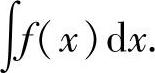
另外,这个定理还告诉我们,一个三角级数 有资格成为某个可积函数的傅里叶级数的必要条件是
有资格成为某个可积函数的傅里叶级数的必要条件是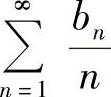 收敛.
收敛.
例如,级数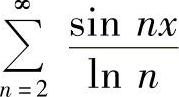 虽然在(-∞,+∞)上收敛,但它却不能是任何可积函数的傅里叶级数.
虽然在(-∞,+∞)上收敛,但它却不能是任何可积函数的傅里叶级数.
4)傅里叶级数逐项求导定理:设f在[-π,π]上连续、按段光滑,且
若f′在[-π,π]上按段光滑,则下面的逐项求导公式成立:
若f′(x)在[-π,π]上连续,则有
进而,若还有f′(-π)=f′(π),则上式对x=±π也成立.
傅里叶级数的部分和Sm(x)的性质以及由它导出的贝塞尔(Bessel)不等式和巴塞伐尔(Parseval)等式在此不再赘述.
例5.59 求f(x)=x3在区间[0,2π]上的傅里叶级数展开式,并由此证明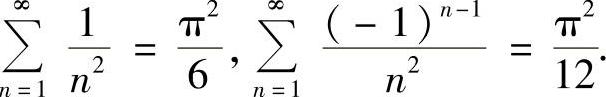
解 因为f(x)在[0,2π]上可积,所以可展开成傅里叶级数.而
故
显然,当x∈(0,2π)时,f(x)=x3连续,故
当x=0时,级数收敛于f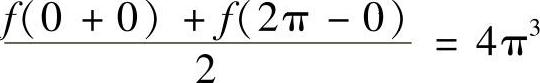 .于是由式(1)可得
.于是由式(1)可得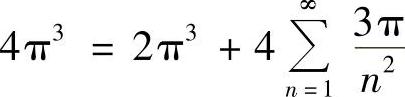 , 即
, 即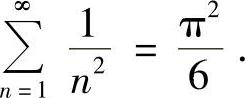
再在式(1)中,令x=π,可得
例5.60 求和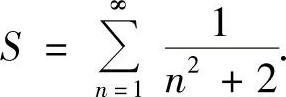
解 考虑函数f(x)=e2x,x∈[0,2π).将f(x)展开成傅里叶级数,则
当n≥1时,
所以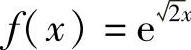 的傅里叶级数为
的傅里叶级数为
由收敛定理,上面的级数在x=0处收敛于
即
例5.61 设
(1)求f的傅里叶级数展开式;
(2)讨论f的傅里叶级数在(-π,π]上是否收敛于f,是否一致收敛于f?
解 (1)由于f在(-π,π)上为奇函数,故
所以f的傅里叶级数展开式为
(2)因为f在(-π,π)上除x=0外都连续,故当x∈(-π,π),且x≠0时,有
又当x=0时,级数收敛于
当x=π时,级数收敛于
由此可见,f的傅里叶级数在(-π,π]上收敛于f.
由于f在(-π,π]上不连续,由连续性定理,若级数在(-π,π]上一致收敛于f,这就与f的不连续性相矛盾,故f的傅里叶级数在(-π,π]上不一致收敛于f.
例5.62 设f(x)是以2π为周期的连续函数,an,bn是傅里叶系数,求函数
的傅里叶系数An,Bn,并利用F(x)的展开式证明巴塞伐尔等式:
解 ∀x∈R,有
即F(x)是以2π为周期的函数,而F(x)的连续性显然.
即F(x)是偶函数.于是,函数F(x)的傅里叶系数
对内层积分作变量替换t+x=y,注意到f的周期性,有
于是
故
在上式中,令x=0,可得巴塞伐尔等式:
注5.9 本例中给出的F(x)称为函数f(x)的卷积,它具有许多好的性质.有兴趣的同学可参看任何一本傅里叶分析的教材或专著.另外,巴塞伐尔等式是熟知的结果,利用它很容易证明傅里叶级数的唯一性定理.
例5.63 证明: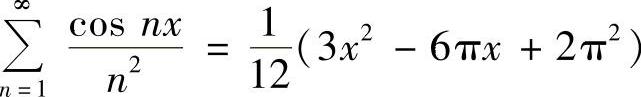 ,x∈[0,π].
,x∈[0,π].
证明 这类题目不能把它视为级数求和,而应把它看成右端函数的傅里叶展开.
记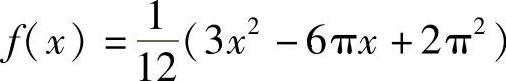 ,从欲证的等式可以看出,需将f(x)在[0,π]上展开成余弦级数.为此,只需将g(x)=3x2-6πx在[0,π]上展开成余弦级数即可.而
,从欲证的等式可以看出,需将f(x)在[0,π]上展开成余弦级数.为此,只需将g(x)=3x2-6πx在[0,π]上展开成余弦级数即可.而
由傅里叶级数收敛定理,有
即
例5.64 (1)设f(x)以2π为周期,在(0,2π)内有界,证明:若f(x)↓,则bn≥0;若f(x)↑,则bn≤0 (n=1,2,…);
(2)设f′(x)在(0,2π)内有界,证明:若f′(x)↑,则an≥0;若f′(x)↓,则an≤0 (n=1,2,…);(https://www.xing528.com)
(3)设f(x)在[0,2π]上连续,证明:若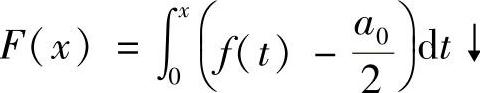 ,则an≥0;若F(x)↑,则an≤0 (n=1,2,…).
,则an≥0;若F(x)↑,则an≤0 (n=1,2,…).
证明 (1)将[0,2π]n等分,则
注意到当f(x)↓时, ,在区间
,在区间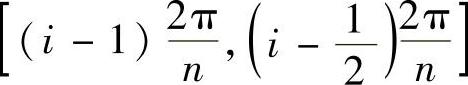 上,sinnx≥0,所以bn≥0.
上,sinnx≥0,所以bn≥0.
类似地可证,当f(x)↑时,bn≤0.
(2)由傅里叶系数的计算公式易得,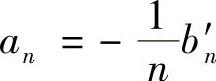 ,这里b′n是f′(x)的傅里叶系数.对f′应用(1)的结论知,若f′(x)↑,则bn′≤0,故an≥0;若f′(x)↓,则bn′≥0,故an≤0.
,这里b′n是f′(x)的傅里叶系数.对f′应用(1)的结论知,若f′(x)↑,则bn′≤0,故an≥0;若f′(x)↓,则bn′≥0,故an≤0.
(3)由f(x)在[0,2π]上连续知,F(x)在[0,2π]上可导,用An,Bn表示F(x)的傅里叶系数,则有
类似地可得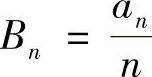 ,n=1,2,….
,n=1,2,….
对F(x)应用(1)的讨论知,若F(x)↓,则an≥0;若F(x)↑,则an≤0.
注5.10 从本例的证明过程可以看出,关键是证明(1).而(1)的证明,也可用第二积分中值定理:
由此易得结论.
例5.65 设f,g在[0,2π]上可积,an,bn和αn,βn分别表示f和g的傅里叶系数,则
证明 写出f+g和f-g的巴塞伐尔等式:
将上两式相减可得结论.
作为例5.65的一个应用,我们用它来证明傅里叶级数的逐项积分定理.
例5.66 设f(x)在[-π,π]上可积,且
则∀[a,b]⊂[-π,π],有
证明 由例5.65知,
上式对[-π,π]上的任一可积函数g(x)都成立.特别地,取
则上式就变成
例5.67 设f(x)在[-π,π]上连续,
求Tn(x)(即确定系数αk,βk),使均方差
最小.
解 设an,bn为f(x)在[-π,π]上的傅里叶系数,而
上式第一、三项为常数.由此可见,当且仅当
αk=ak,βk=bk (k=1,2,…,n),α0=a0时δ最小,最小值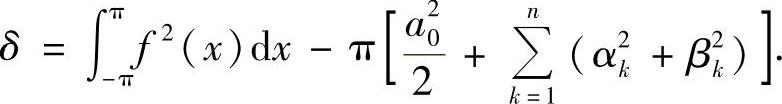
这个结论告诉我们,在均方收敛的意义下,连续函数f(x)的傅里叶三角多项式是所有三角多项式的最佳逼近,并且是一致的.
例5.68 设f(x)在[0,π]上有连续导数,f′(x)在[0,π]上分段光滑,且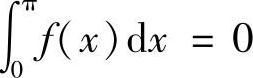 ,试证:
,试证:
证明 将f(x)偶延拓到[-π,0]上,由已知条件,延拓后的函数能在[-π,π]上展开成傅里叶级数,且a0=0,bn=0,
逐项微分可得
二者均为傅里叶展开式.利用巴塞伐尔等式:
故
类题 设f(x)在[0,π]上二阶连续可导,f(0)=f(π)=0.
试证明:级数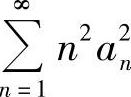 收敛(华南理工).
收敛(华南理工).
提示 将f(x)奇延拓到[-π,0]上,则f′(x)是[-π,π]上的偶函数,而且能展开成傅里叶级数.
记f′(x)在[-π,π]上的傅里叶系数分别为An,Bn则A0=0,Bn=0,n=1,2,….
由
可得
An=nan,n=1,2,….
由巴塞伐尔等式,有
即级数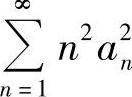 收敛.
收敛.
例5.69 设f(x)在[a,b]上可积且平方可积,{φn(x)}是[a,b]上的标准正交系,即
记
证明:级数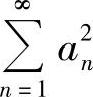 收敛,且
收敛,且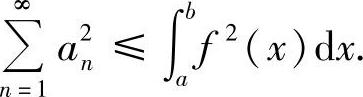
证明 令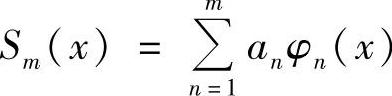 ,则
,则
即
这表明级数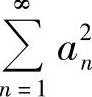 的部分和有上界,所以
的部分和有上界,所以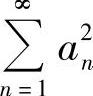 收敛,且
收敛,且
例5.70 设f(x)在[0,π]上连续,且对任意的n≥1,均有
证明:f(x)为常值函数(南大).
证明 先将f(x)偶延拓到[-π,π]上,然后再作周期为2π的周期延拓到(-∞,+∞)上,则f(x)的傅里叶系数bn=0,n=1,2,….
由已知条件,an=0,n=1,2,….所以,f(x)的傅里叶展开为
由傅里叶级数的收敛定理,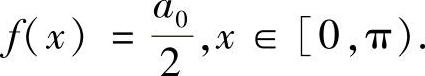 再由f(x)在[0,π]上连续性,有
再由f(x)在[0,π]上连续性,有 ,x∈[0,π].
,x∈[0,π].
类题 设f(x)在[-π,π]上连续,f(-π)=f(π),且
证明:f(x)≡0,∀x∈[-π,π].
提示 用巴塞伐尔等式.
由已知条件,an=0(n=0,1,…),bn=0(n=1,2,….).由于f(x)在[-π,π]上连续,所以巴塞伐尔等式成立:
由连续函数的性质知,f2(x)≡0,即f(x)≡0,∀x∈[-π,π].
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




