常用的方法:
1)收敛原理,即正项级数收敛的充要条件是它的部分和数列有上界;
2)比较法.在使用比较法判定级数敛散性时,首先要对级数的敛散性有个精确地估计,然后通过不等式的放大或缩小找到合适的比较级数;
3)根式判别法;
4)比式判别法.
根式判别法和比式判别法都是比较法的具体化,它们是以几何级数作为比较级数而建立的.另外,凡是能用比式判别法判别的级数一定能用根式判别法判别,但反之不行!换言之,就是根式判别法比比式判别法有更广的适用范围.
除了上述大家熟悉的判别法外,下面我们再介绍几个判别法.
5)拉贝(Raabe)判别法.
对正项级数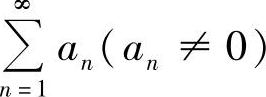 ,记
,记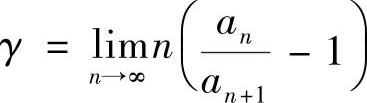 ,则γ>1时,级数收敛;当γ<1时,级数发散.
,则γ>1时,级数收敛;当γ<1时,级数发散.
6)高斯(Gauss)判别法.
对正项级数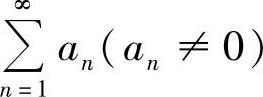 ,若
,若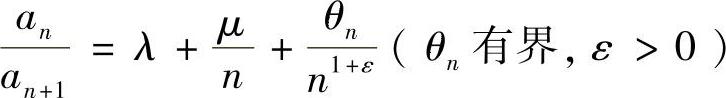 ,则当λ>1或λ=1而μ>1时,级数收敛;当λ<1或λ=1而μ≤1时,级数发散.
,则当λ>1或λ=1而μ>1时,级数收敛;当λ<1或λ=1而μ≤1时,级数发散.
7)柯西判别法.(https://www.xing528.com)
若{an}为递减正数列,则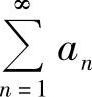 与
与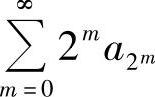 同敛散.
同敛散.
8)对数判别法.
对正项级数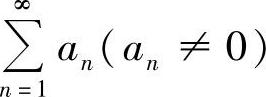 ,若∃α>0及自然数N,当n>N时,有
,若∃α>0及自然数N,当n>N时,有
则级数收敛;
若存在自然数N,使当n>N时,
则级数发散.
9)柯西积分判别法.
设f(x)在[1,+∞)上非负且递减,则 与
与 同敛散.
同敛散.
需要特别说明的是:拉贝判别法和对数判别法都是以p级数作为比较级数而建立的,而高斯判别法则是以比p级数收敛得更慢的级数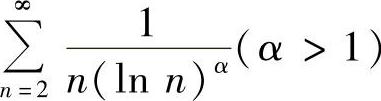 作为比较级数而建立的.从比式判别法(或根式判别法)到拉贝判别法(或对数判别法)再到高斯判别法虽然适用范围一个比一个更广泛,但由于我们找不到(事实上也不存在)一个收敛最慢的级数作为比较级数,因此也就无法建立适用于一切正项级数的判别法.
作为比较级数而建立的.从比式判别法(或根式判别法)到拉贝判别法(或对数判别法)再到高斯判别法虽然适用范围一个比一个更广泛,但由于我们找不到(事实上也不存在)一个收敛最慢的级数作为比较级数,因此也就无法建立适用于一切正项级数的判别法.
另外,我们还会经常用到如下的
斯特林(Stirling)公式:n!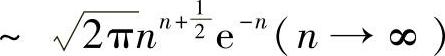 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




