技巧揭秘数学分析定积分计算方法

（1）设f（x）是以T为周期的连续函数，a为任意常数，则

（2）设f（x）在[a，b]上连续，则

这个公式对不易求出原函数的定积分，使用起来非常有效！在后面我们将举例来说明这一点.

（3）设f（x）在[-l，l]（l>0）上连续，则

（3）是（2）的特例.

例4.15　求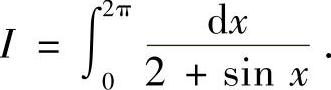

分析　直接作变换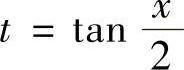导致失败的原因是：在[0，2π]上上述变换不满足换元法的条件.正确的作法是，先把[0，2π]分成若干个小区间，把不在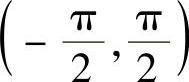内的部分平移至其内，然后再用上述变换.

解　由于被积函数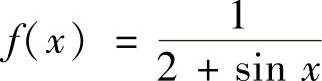是以2π为周期的连续函数，故有

对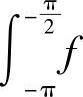，作变换t=-π-x，则有

即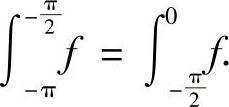

对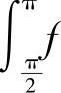f，作变换t=π-x，类似于上面，则有

于是有

令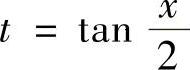，则有

例4.16　求下列定积分

分析　利用计算技巧的（2）.

解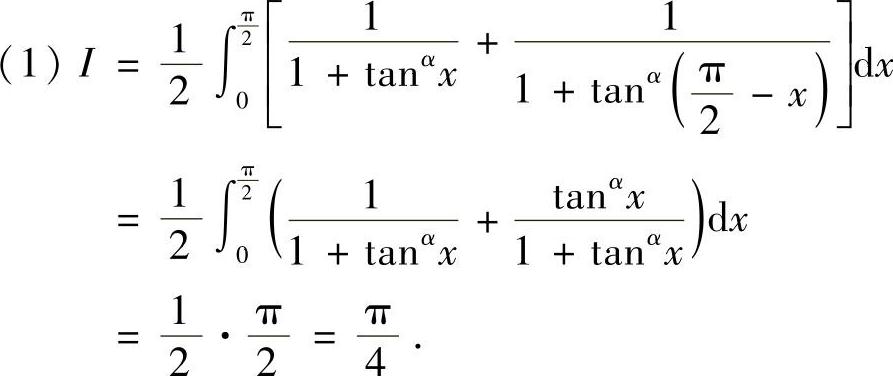

（3）先作变换：x=tant，则可将积分化为

用这种方法可以很快求出下面的积分.

类题　计算下列积分

例4.17　设函数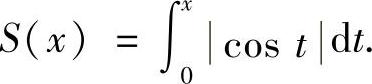

（1）当n为正整数，且nπ≤x<（n+1）π时，证明：

2n≤S（x）<2（n+1）；

（2）.

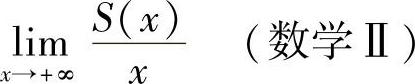证明　（1）因为cost≥0，且nπ≤x<（n+1）π，所以

又因为cost是以π为周期的函数，所以(https://www.xing528.com)

所以当nπ≤x<（n+1）π时，有2n≤S（x）<2（n+1）.

（2）由（1）知，当nπ≤x<（n+1）π，有

令x→+∞可得.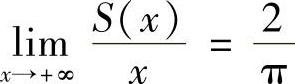

注4.5　本例的一般形式为：设f（x）是以T为周期的非负连续函数，则

事实上，∀x>0，∃n∈N+，使得nT≤x<（n+1）T.而f（x）≥0，故有

于是有

令x→+∞，可得结论.

类题　求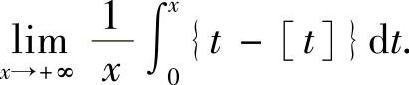

例4.18　求下列积分

分析　分段函数求积分，其方法是：将积分区间从分段点分开.

解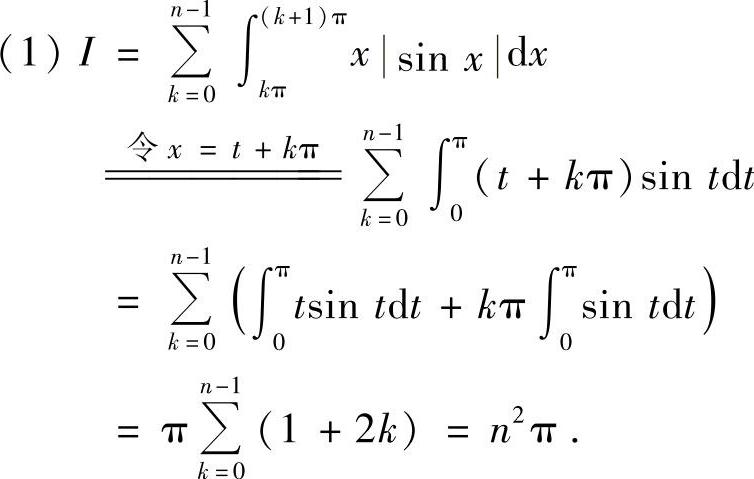

（2）因为被积函数是偶函数，所以

例4.19　设函数f（x）在（-∞，+∞）内满足f（x）=f（x-π）+sinx且f（x）=x，x∈[0，π）.计算.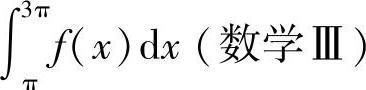

解法1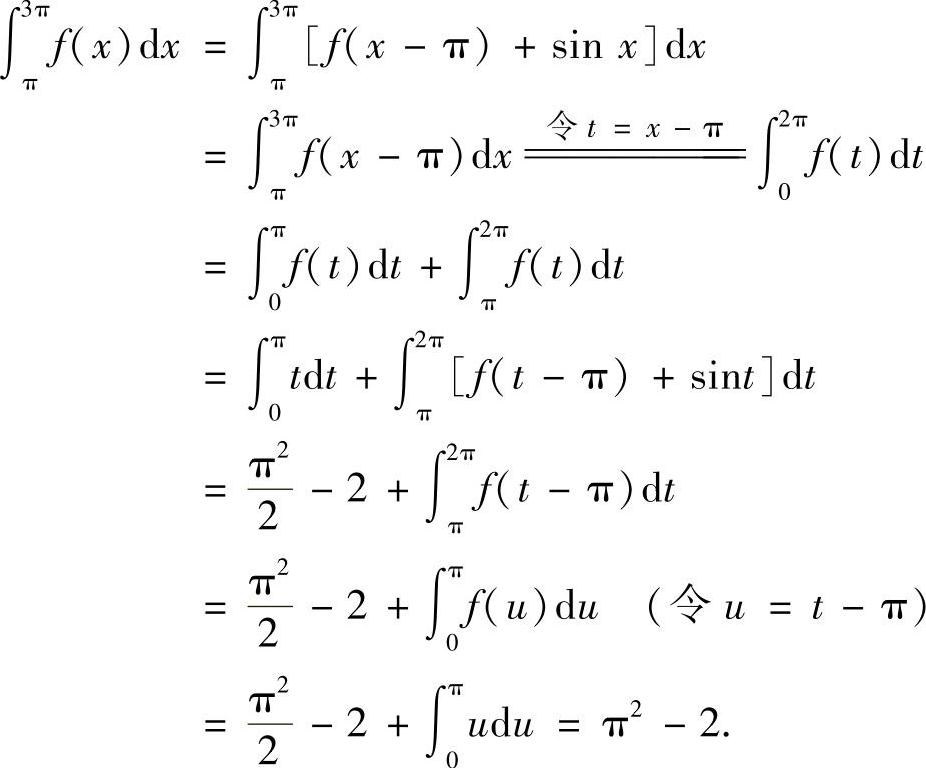

解法2　当x∈[π，3π）时，有

故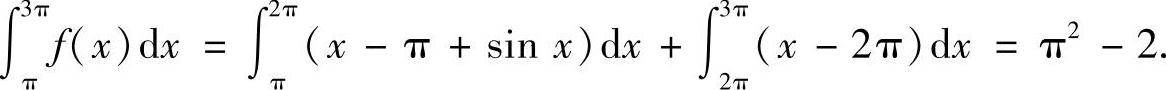

例4.20　计算积分

分析　当被积函数中含有“变限积分”时，常用的求解方法：①分部积分法；②化成二重积分，然后交换积分的顺序.

解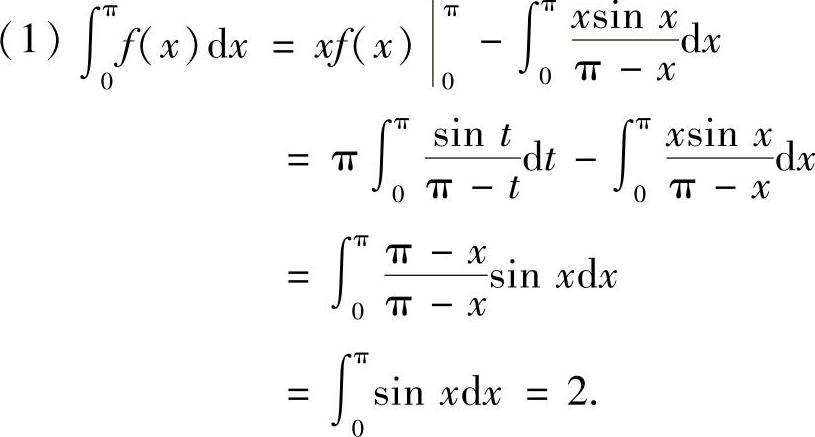

或用二重积分交换顺序来计算.

由x，t所满足的不等式组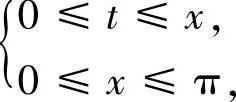画出积分区域的草图.改变积分的顺序：

或用二重积分交换顺序来计算.

由x，t所满足的不等式组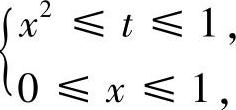画出积分区域的草图.改变积分的顺

序