【摘要】：相对而言，在不定积分中对此不作过多的强调，而自然认为所作的变换是在“可行”的区间上进行的.例如，求若令，则，，且x=0，2π时，t=0.这样有：这是一个错误的结果，正确的解法我们将在后面给出.定理3若u，v在[a，b]上具有连续导数u′，v′，则在使用定积分的分部积分公式时，要特别注意对右端第一项的理解，否则将会导致错误的结论.看下面的例子：由此导致0=-1的谬误，问题出在什么地方呢？请同学们指出来.
定理1 （牛顿-莱布尼茨公式）若f（x）在[a，b]上连续，则对f（x）在[a，b]上的任何原函数F（x）都有
牛顿-莱布尼茨公式可以作如下的减弱.
命题4.1 若f（x）在[a，b]上可积，且有原函数F（x）（即F′（x）=f（x）），则
命题4.2 若f（x）在[a，b]上可积，F（x）在[a，b]上连续，在（a，b）内除有限个点外均有F′（x）=f（x），则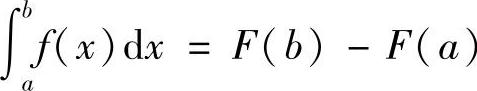
.
命题4.2在下一段中我们将给予证明.
定理2 （换元法）设f（x）在[a，b]上连续，代换x=φ（t）满足条件：
（1）φ（t）在[α，β]或[β，α]上单调且有连续的导数；
（2）当t∈[α，β]或[β，α]时，a≤φ（t）≤b且φ（α）=a，φ（β）=b，(www.xing528.com)
则有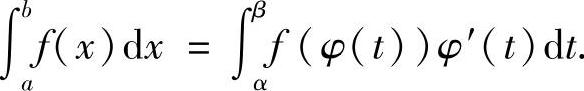
定积分的换元法和不定积分的换元法在形式上是类似的，但它们还存在着差异.这是因为定积分的换元必须和积分区间联系起来，不仅要考虑换元后的积分是否好算，而且还要考虑在积分区间上所作的换元变换是否可行！相对而言，在不定积分中对此不作过多的强调，而自然认为所作的变换是在“可行”的区间上进行的.
例如，求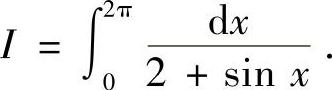
若令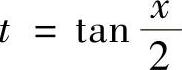
，则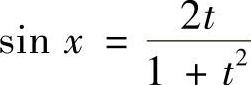
，
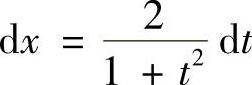，且x=0，2π时，t=0.这样有：
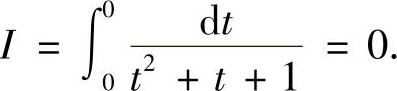这是一个错误的结果，正确的解法我们将在后面给出.
定理3 （分部积分法）若u（x），v（x）在[a，b]上具有连续导数u′（x），v′（x），则
在使用定积分的分部积分公式时，要特别注意对右端第一项的理解，否则将会导致错误的结论.看下面的例子：
由此导致0=-1的谬误，问题出在什么地方呢？请同学们指出来.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
