带余项的泰勒公式及巨大差异

1.带有佩亚诺（Peano）型余项的泰勒公式：设f（x）在x₀点n阶导数存在，则

2.带有格拉朗日型余项的泰勒公式：设f（x）在（a，b）内有连续的n阶导数，n+1阶导数f^（n+1）（x）存在，x，x₀∈（a，b），则

其中ξ介于x₀与x之间.

带有佩亚诺型余项的泰勒公式要求x→x₀，而带有拉格朗日型余项的泰勒公式没有这个要求.这也导致了两类公式在证明上的巨大差异，前者可用洛必达法则证明，而后者要用柯西中值定理证明.另外，在使用上前者主要用于定性分析，后者主要用于定量计算.如，应用泰勒展开计算极限，就不需要对余项作定量的计算，因此，用佩亚诺型余项即可.

显然，当x→x₀时满足拉格朗日型余项蕴含着满足佩亚诺型余项.

当遇到与高阶导数（二阶以上）有关的命题时，一般应考虑用泰勒公式.一个困难而关键的问题是：如何选取点x₀？一般来说，选取使f^（i）（x₀）=0（i=1，2，…，k）的点，比如f（x）的极值点等.

3.基本公式（带有佩亚诺型余项）.

例3.40　设f（x）在原点的邻域内二次可导，且

（1）求f（0），f′（0），f″（0）；

（2）求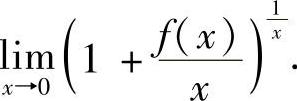

解　将f（x）在点0展开成带有佩亚诺型余项的泰勒公式

（1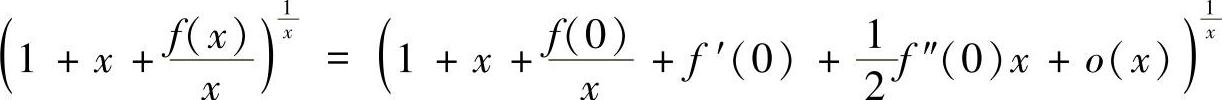），由已知的极限，必须有f（0）=f′（0）=0.于是有

由此可得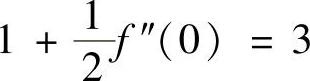，即f″（0）=4.

（2）由（1）有

例3.41　设函数f（x）在x=0的某邻域内具有二阶连续导数，且f（0）≠0，f′（0）≠0，f″（0）≠0.证明：存在唯一的一组实数λ₁，λ₂，λ₃，使得当h→0时，λ₁f（h）+λ₂f（2h）+λ₃f（3h）-f（0）是比h²高阶的无穷小（数学Ⅱ）.

解　由泰勒公式可知，当h→0时，有

于是

由题意，λ₁，λ₂，λ₃应满足下面的代数方程组

由方程组的理论易知，关于λ₁，λ₂，λ₃的方程组存在唯一的解，即存在唯一的一组实数λ₁，λ₂，λ₃，使当h→0时，λ₁f（h）+λ₂f（2h）+λ₃f（3h）-f（0）是比h²高阶的无穷小.

例3.42　确定常数a，b，使当x→0时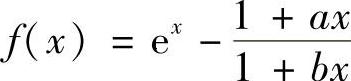，为x的3阶无穷小.

证明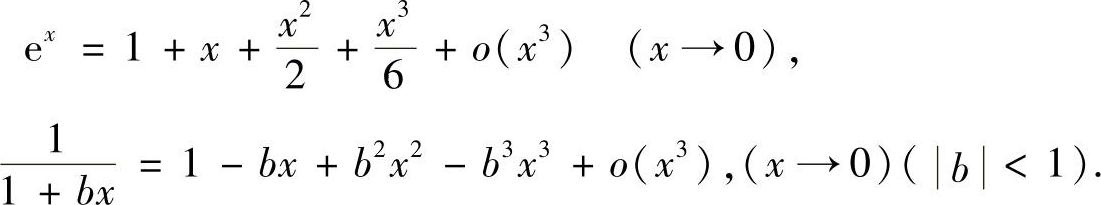

于是

欲使f（x）为三阶无穷小量，必须有

解之得，.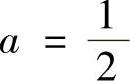

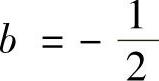例3.43　设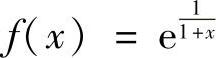，求f（5）（0）.

解 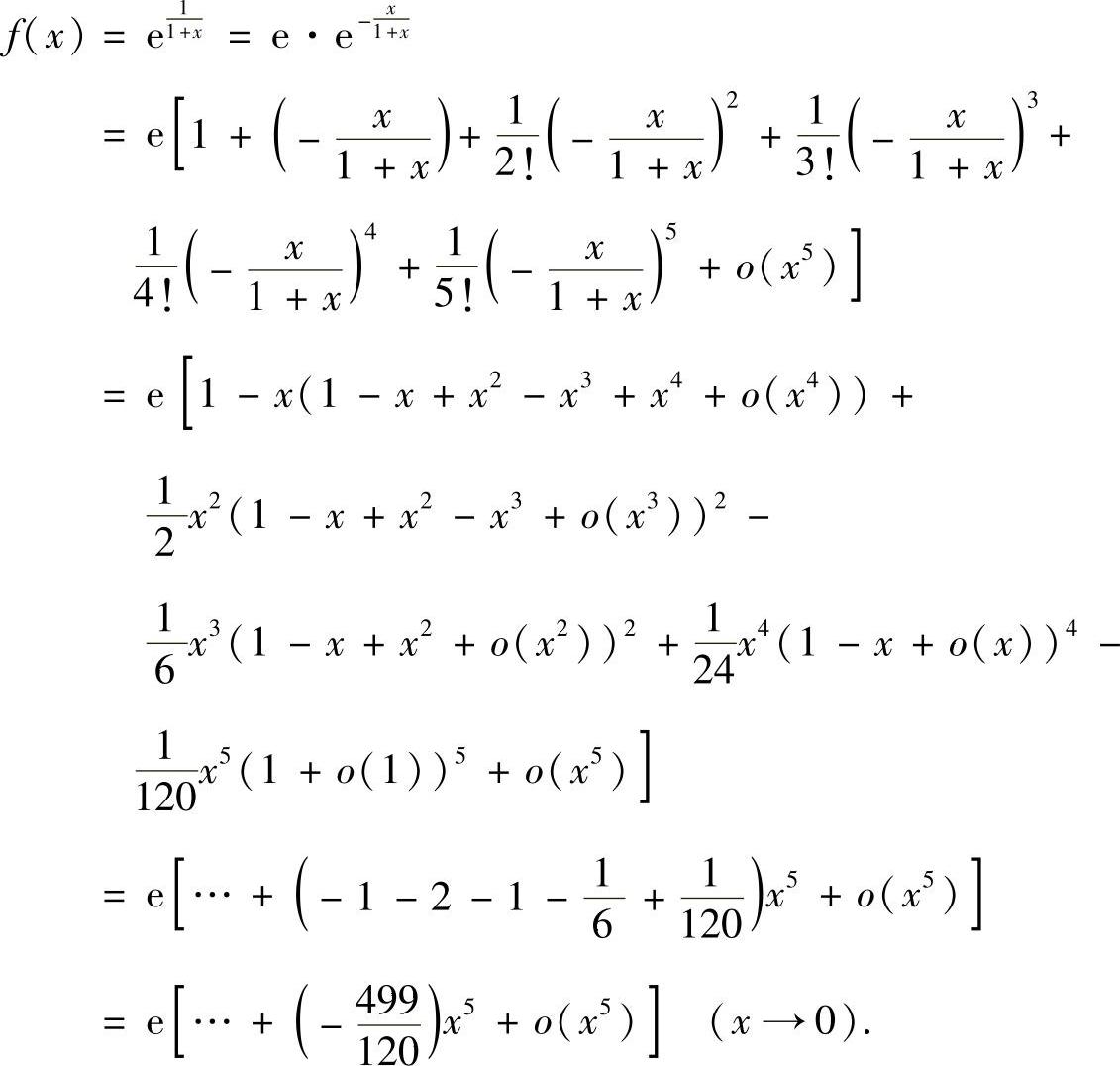所以

例3.44　设f（x）在[0，1]上有二阶连续导数，且f（0）=f（1）=0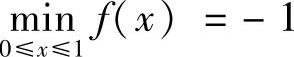，，证明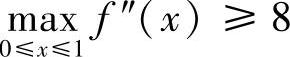：（北师大）.

证法1　用泰勒公式证明.由题设f（x）在[0，1]上的最小值必在（0，1）内取到，即∃c∈（0，1），使f（c）=-1.由费马引理知，f′（c）=0.将f（x）在c点作泰勒展开，有

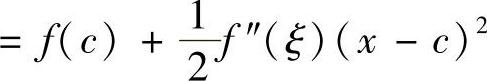，　其中ξ在x与c之间.

在上式中分别令x=0，x=1可得

将两式相加可得

f″（ξ₁）c²+f″（ξ₂）（1-c）²=4.

由此可知，

注意到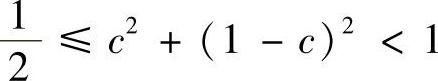，可得

证法2　用辅助多项式方法证明.构造辅助多项式P（x）=4x（x-1），满足条件P（0）=P（1）=0，且.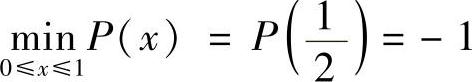

令F（x）=f（x）-P（x）=f（x）-4x（x-1），则F（0）=F（1）=0，且F（x）在[0，1]上有二阶连续导数.由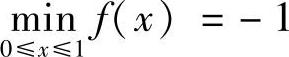知，∃c∈（0，1）使得f（c）=-1.

若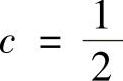，则F（c）=0；

若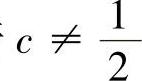，则F（c）=f（c）-P（c）<0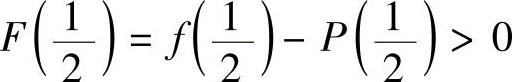，，由连续函数的介值定理知，∃η∈（0，1），使得F（η）=0.

对F（x）分别在[0，η]和[η，1]上应用罗尔定理知，∃ξ₁∈（0，η）和ξ₂∈（η，1）使得F′（ξ₁）=F′（ξ₂）=0.再对F′（x）在[ξ₁，ξ₂]上应用罗尔定理知，∃ξ∈（ξ₁，ξ₂）使得F″（ξ）=0，即f″（ξ）=8.从而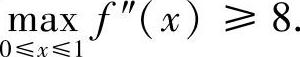

注3.8　本例的证法2应用了所谓的辅助多项式法.若题目的结论要求证明“∃ξ∈（a，b），使得‘f^（n）（ξ）=k　（n≥2，k≠0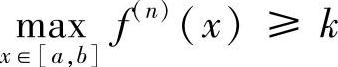）’或‘’或‘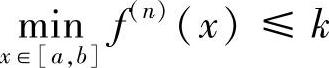’”，那么我们可构造一个n次多项式P（x）让它满足题目中f（x）的所有条件，然后令F（x）=f（x）-P（x），最后对F（x）多次使用罗尔定理即可.例3.22、3.23用的正是这种方法.

在本例中，由结论知，P（x）应是一个二次多项式.由f（0）=f（1）=0可知，x和（x-1）都是P（x）的因式，故可令P（x）=Ax（x-1）（A>0，待定）.再由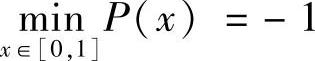可得A=4，从而P（x）=4x（x-1）.

下面再看两个这类题目.

类题1 设f（x）在闭区间[-1，1]上具有三阶连续导数，且f（-1）=0，f（1）=1，f′（0）=0.证明：∃ξ∈（-1，1），使f（ξ）=3 （数学Ⅱ）.

分析 由结论知，这里的辅助多项式P（x）是三次的.又由f（-1）=0知，可设P（x）=（x+1）（Ax²+Bx+C），其中A，B，C待定.这里有三个常数要确定，但仅要求P（1）=1，P′（0）=0是不够的，为此我们附加条件P（0）=f（0）（这是为了使F（x）能在[-1，0]和[0，1]上应用罗尔定理）.通过简单计算可求得

类题2 设f（x）在[0，1]上具有三阶连续导数，且f（0）=1，f（1）=2，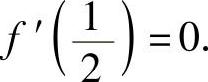

证明：∃ξ∈（0，1），使f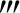（ξ）≥24（数学Ⅰ，副题）.

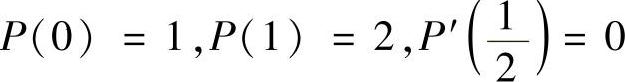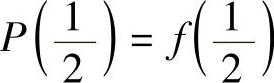分析 这里P（x）是三次的，设为P（x）=Ax³+Bx²+Cx+D.由题设条件让P（x）满足和附加条件，可得

另外，这两个类题仿本例的证法1用泰勒公式做也不复杂，请同学们一试.

例3.45 设f（x）在[0，1]上有一阶连续导数，证明存在c∈（0，1），使

分析 这个题目乍一看起来无从下手，因为中值定理无法直接将导数和积分联系起来，而泰勒公式似乎也无法应用.但是不要忘记了f（x）的原函数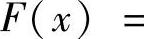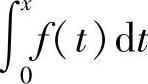，这样就可将结论改写成

问题就变得明了啦！这是处理这类问题的常用手段.

证明 令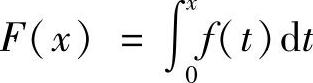，则F（x）在[0，1]上有二阶连续导数.对F（x）应用泰勒公式，有

在上式中取x=1，即得

例3.46 设f（x）在[0，2]上二次可微，∣f（x）∣≤1，∣f″（x）∣≤1，∀x∈[0，2].证明：∀x∈[0，2]，有∣f′（x）∣≤2（东南大学）.

证明 将f（x）在x点作泰勒展开，得

将上两式相减，得

即

其中x²+（2-x）²在[0，2]上的最大值为4.

类题1 设f（x）在[0，1]上具有二阶导数，且f（x）≤a，f″（x）≤b，c是（0，1）内任一点，则.

类题2 设f（x）在[0，1]上具有二阶导数，且f（1）=f（0），f″（x）≤M.证明：∀x∈[0，1]，有.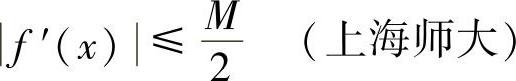

下面的两个例子是例3.47在无限区间上的推广.

例3.47 设f（x）在（a，+∞）上二次可微，且∣f（x）∣，∣f″（x）∣在（a，+∞）上分别有有限的上确界M₀，M₂.证明∣f′（x）∣在（a，+∞）上也有界且其上确界M₁满足不等式

M²₁≤4M₀M₂. （1）

证明　若M₂=0，则f″（x）=0.由f（x）有界可知，f（x）=常数，故M₁=0，此时式（1）显然成立.

设M₂>0，∀x∈（a，+∞）及h>0，由泰勒公式有

由此可得

记

易知，g（h）在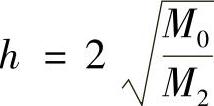处达到最小值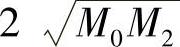.于是有

对上式取上确界即得式（1）.

注3.9 式（1）通常称为内插不等式，它在实分析中经常会用到，并且系数4是最好的.例如，在（-1，+∞）上考虑函数

容易验证：M₀=1，M₁=4，M₂=4，即M²₁=4M₀M₂.若取c<4，对这个函数来说，将有

M²₁>cM₀M_2.

也就是说，若式（1）中的系数小于4，那么式（1）将可能不再成立.

例3.48 设f（x）在（-∞，+∞）上二次可微，且

证明：M²₁≤2M₀M₂（北大）.

证明 对∀x∈（-∞，+∞）及任意的实数h，由泰勒公式，有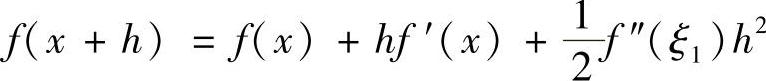，_ξ1在x与x+h之间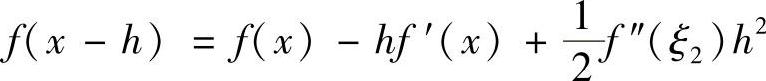，，ξ₂在x与x-h之间.将上两式相减得

所以

2h∣f′（x）∣≤2∣hf′（x）∣≤2M₀+M₂h²，∀x，h∈R.

固定h，对上式关于x取上确界，可得

M_2h²-2M₁h+2M₀≥0，∀h∈R.

上式是关于h的二次三项式，由其判别式Δ≤0可得

M²₁≤2M₀M₂.

例3.49　设函数f（x）在（-∞，+∞）上有三阶导数，并且f（x），f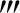（x）在（-∞，+∞）上有界.证明：f′（x）和f″（x）也在（-∞，+∞）上有界（北师大）.

证明　设∣f（x）∣≤M₀，∣f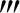（x）∣≤M₃，由泰勒公式，有(www.xing528.com)

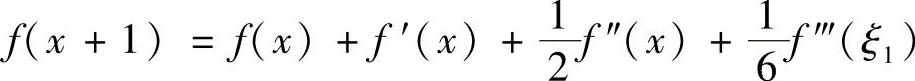，其中ξ₁在x与x+1之间，

（1）

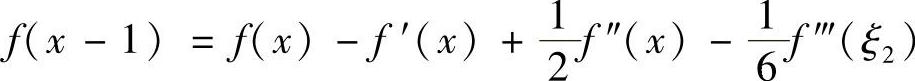，其中ξ₂在x-1与x之间，

（2）

式（1）+式（2）可得

故

至于f′（x）的有界性，可利用已证得f″（x）有界和上例的结论立即可得，或直接证明.将式（1）-式（2）可得

故

例3.50　设f（x）有二阶连续导数，且∀x∈R，∀h>0，成立

f（x+h）+f（x-h）-2f（x）≥0.

证明：∀x∈R，f″（x）≥0（北师大）.

证明　将f（x±h）在x处作泰勒展开，有

将上两式相加，并除以h²，由所给的不等式可得

f″（x）+o（1）≥0.

令h→0⁺，有f″（x）≥0.

例3.51　若f（x）在R上存在三阶连续导数，且∀h>0，有

证明：f（x）至多是二次多项式.

证明　只需证：f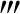（x）≡0，∀x∈R.

将f（x+h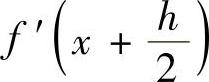），在x处作泰勒展开

将上两式代入所给的等式中，比较两端可得

当h→0时，有ξ，η→x.由三阶导数的连续性，有

例3.52 若f（x）在R上存在任意阶导数，且∃L>0，∀x∈R，∀n∈N+，有

f^（n）（x）≤L.又∀n∈N⁺，有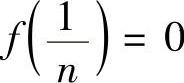，证明：f（x）≡0，∀x∈R.

对f（x）在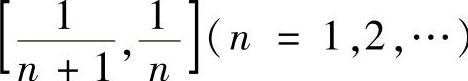上应用罗尔定理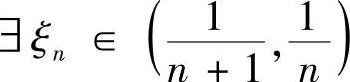，，ξ_n→0（n→∞），使f′（ξ_n）=0 （n=1，2，…）.

又因为f′（x）在0点连续，所以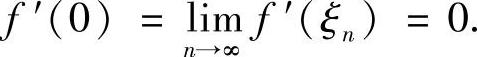

同理可证：∀n∈N⁺，f^（n）（0）=0.

∀x∈R，将f（x）在点0处展开成泰勒公式，有

而

由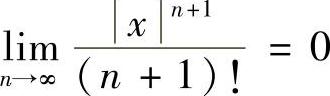可知，f（x）=0.于是∀x∈R，都有f（x）=0.

下面看一个难度大些的题目.

例3.53 设f（x）在闭区间[a，b]上二次可微，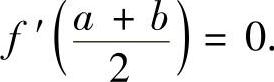

（1） 试证存在ξ∈（a，b），使得

说明系数4是最好的，即对任何M>4，总可找一具体的[a，b]及其上满足条件的f（x），使对一切ξ∈（a，b），都有

（2） 如果再设f（x）≢常数，试证存在η∈（a，b），使

证明 （1）将f（x）在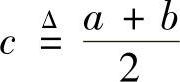点作泰勒展开，

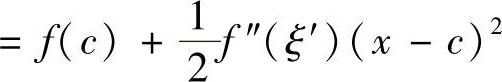， 其中ξ′在x与c之间.

在上式中分别令x=a，x=b可得

将上两式相减，并注意到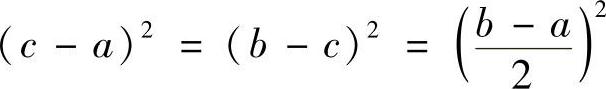可得

令∣f″（ξ）∣=max{∣f″（ξ₁）∣，∣f″（ξ₂）∣}，即得式（1）成立.

下面我们举例说明式（1）中的系数4是最好的.

取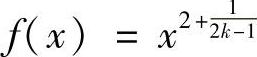，k∈N⁺，x∈[-1，1].显然f（x）在[-1，1]上二次可微，f′（0）=0且f（1）-f（-1）=2.而

欲使

成立，必须有

因为k→∞时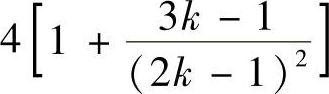，单调递减趋向于4，所以无论M-4>0多么小，都存在适当大的自然数k，使得式（4）成立.也就是说，有相应的f（x）使得∀x∈[-1，1]，都有式（3）成立.

（2） 若f（x）≢常数，由f′（c）=0可知，f′（x）≢常数，从而f″（x）≢0.记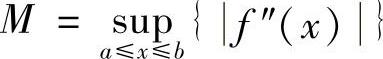，则显然M>0.

若M=+∞，则式（2）显然成立；

若M<+∞，且f″（x）≢M，则有

上面最后一个不等式出现严格不等号是因为在∣f″（x）∣≢M时，

∣f′（x）∣=∣f′（x）-f′（c）∣≤M∣x-c∣

至少在一点成立严格不等式，而由f′（x）的连续性知，积分后便出现严格不等式；

若∣f″（x）∣≡M，由f′（x）的连续性及f′（c）=0可知，应有

f′（x）=±M（x-c），

所以

此时f（x）是以x=c为对称轴的抛物线，故f（a）=f（b），而

是显然的.

由上确界的性质，无论哪一种情形，都存在η∈（a，b），使式（2）成立.

下面的例题是关于“中值点”极限性质的.

例3.54 设f（x）在（a-δ，a+δ）（δ>0）上有n+1阶导数且f^（n+1）（a）≠0及f′（a）=f″（a）=…=f^（n）（a）=0.由微分中值定理

f（a+h）-f（a）=f′（a+θh）h，0<θ<1，∣h∣<δ. （1）

求证：.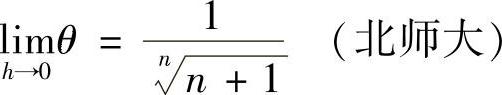

证明　将f（a+h）在a点作带有佩亚诺型余项的泰勒展开

对f′（a+θh）在a点作同样的展开，有

将上式代入式（1）可得

比较式（2）、式（3），并注意到f（n+1）（a）≠0，有

故

类题1 设h>0，函数f在U（a，h）内具有n+2阶连续导数，且f^（n+2）（a）≠0，f在U（a，h）内的泰勒公式为

证明：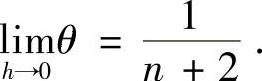

提示 对f（a+h）在a点作（n+2）阶泰勒展开，对f（^n+1）（a+θh）在a点作1阶泰勒展开.

类题2 设f（x）在（-1，1）内具有二阶连续导数，且f″（x）≠0.证明：

（1）∀x∈（-1，1）且x≠0，存在唯一的θ（x）∈（0，1），使得

f（x）=f（0）+xf′（θ（x）x）；

（2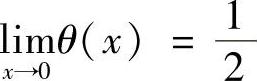）.（数学Ⅰ）.

下面的例题是用高阶导数判断极值的一个非常有用的结论，希望同学们记忆它.

例3.55 设n≥2，r>0，f（n）（x）在[a-r，a+r]上连续，并设f^（k）（a）=0 （1≤k≤n-1），f^（n）（a）≠0.证明：

（1）当n为偶数时，a是极值点；

（2）当n为奇数时，a是拐点.

证明 （1）因为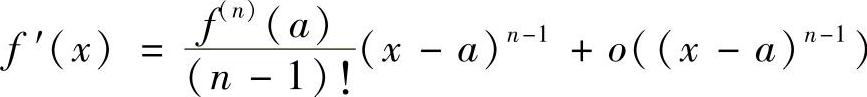，所以

又因f^（n）（a）≠0，故∃δ>0，使当x∈U°（a，δ）时，有

由式（1）知，当n为偶数时，f′（x）（x-a）与f^（n）（a）在U°（a，δ）上同号，因此a为极值点.

（2）因为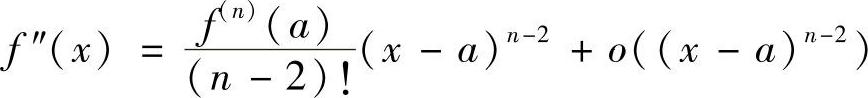，所以

又因f^（n）（a）≠0，故∃δ>0，使当x∈U°（a，δ）时，有

由式（2）知，当n为奇数时，f″（x）（x-a）在U°（a，δ）上不变号，因此x=a是拐点.