高阶导数证明|考研数学分析|名校真题挑选

1.熟记常用的高阶导数公式

2.求高阶导数常用的方法.

（1）拆、合法

当遇到的表达式不易直接求导时，常将它拆开成若干项之和，然后利用熟知的结果或先求导一次，然后合成一项，再利用熟知的结果.

（2）莱布尼茨公式法

若要求导的函数是两个函数相乘，而每一个函数的高阶导数都是熟知的结果或求导次数不是太高，则可直接应用莱布尼茨公式

（3）数学归纳法

当高阶导数不能一下求出时，可先求出前几阶导数，总结归纳出其n阶导数的表达式，然后用数学归纳法加以证明.

（4）递推公式法

先求出前几阶（一般是两阶）导数化成等式，然后两边同时求高阶导数，得到一般形式的递推关系式.

（5）泰勒公式法

欲求f（x）在x=a处的n阶导数值，可将f（x）在a点作泰勒展开：

由此可求出f^（n）（a）.

例3.11 求y=e^αxcosβx的n阶导数.

解 y′=e^αx（αcosβx-βsinβx）

用数学归纳法，易证：

例3.12 设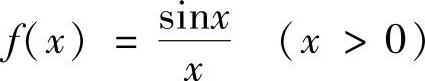，记

其中P_n（x），Q_n（x）是关于x的多项式，求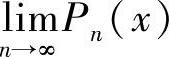和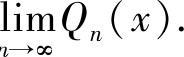

解 由莱布尼茨公式，有

由此可知，

和

所以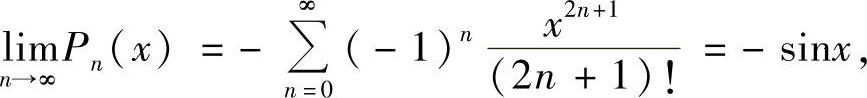

例3.13 证明：函数

在x=0处存在任意阶导数，且f^（n）（0）=0 （n=1，2，…）.

证明 当x≠0时，

其中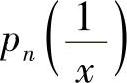是关于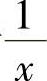的3n次多项式（这不难用数学归纳法证明）.

假设f^（n-1）（0）=0，则有

例3.14 用莱布尼茨公式计算y^（n）（0）.

（1）y=arcsinx； （2）y=arctanx.

解　（1）求两阶导数可得

（1-x²）y″=xy′.

对上式两边求n阶导数，得

在上式中，令x=0可得

y^（n+2）（0）=n²y^（n）（0）.

由递推公式，并注意到y（0）=0，y′（0）=1，可得

y^（2k）（0）=0，　y^（2k+1）（0）=[（2k-1）！！]²，k为自然数.

（2）求导一次可得

（1+x²）y′=1.(www.xing528.com)

对上式两边求n阶导数，得

（1+x²）y^（n+1）+2nxy^（n）+n（n-1）y（n^-1）=0.

在上式中，令x=0可得

y^（n）（0）=-（n-1）（n-2）y^（n-2）（0）.

由递推公式，并注意到y（0）=0，y′（0）=1可得：

y^（2k）（0）=0，y^（2k+1）（0）=（-1）^k（2k）！，k为自然数.

例3.15 设f（x）=x¹⁰arctanx，求f^（n）（0）（西北大学）.

解 用泰勒公式，

两边积分可得

由此可得f（x）的泰勒展开式

于是，有

若令2n+11=2l+1，则上式可改写为

综上，我们有

其中l为自然数.

类题 求高阶导数在指定点处的值.

（1）设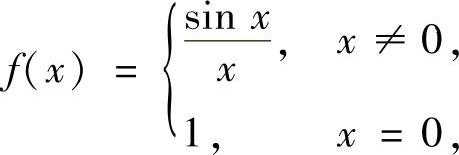 求f^（n）（0）（华东师大）；

（2）设f（x）=x²ln（1+x），求f^（n）（0）（n≥3）（数学Ⅱ）.

提示 （1）由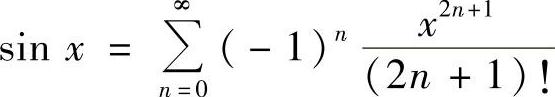，x∈R可得

由此知

（2）由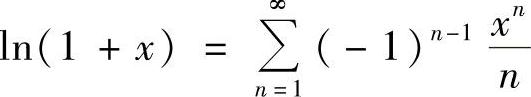，x∈（-1，1]，可得

由此知，

例3.16　设f（x），g（x），p（x）有二阶连续导数，求

（华中师大）.

证明　因为一阶差商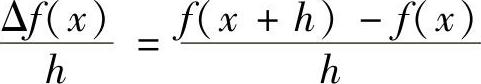逼近一阶导数f′（x）.二阶差商

逼近二阶导数f″（x），所以利用行列式的性质有

例3.17　设f（x）在（-∞，+∞）上三阶可导，证明：存在实数ξ，使得

f（ξ）f′（ξ）f″（ξ）f（ξ）≥0.

证明　若存在一点x₀∈（-∞，+∞）.使得f^（i）（x₀）（i=0，1，2，3）中有一个为零，则结论显然成立.因此，不妨设f^（i）（x）≠0（i=0，1，2，3），∀x∈（-∞，+∞）.

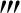不失一般性，假设f（x）>0，∀x∈（-∞，+∞）.这是因为，若f（x）<0，考虑g（x）=f（-x），则g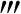（x）=-f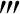（x）>0，而且当η∈（-∞，+∞），使得g（η）g′（η）g″（η）g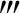（η）>0时，令ξ=-η，则必有f（ξ）f′（ξ）f″（ξ）f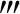（ξ）>0.

进而，不失一般性还可假设f″（x）>0，∀x∈（-∞，+∞）.这是因为，若f″（x）<0，考虑h（x）=-f（x），则h″（x）=-f″（x）>0，而且当ξ∈（-∞，+∞），使得h（ξ）h′（ξ）h″（ξ）h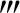（ξ）>0时，必有f（ξ）f′（ξ）f″（ξ）f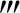（ξ）>0.

于是，我们可在f″（x）>0，f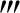（x）>0，∀x∈（-∞，+∞）的假设下证明本题的结论.

由泰勒公式，有

>f′（a）+f″（a）（x-a）→+∞（x→+∞）.

其中η₁在x与a之间.由此可知，存在X₁>a，当x≥X₁时，f′（x）>0.

再由泰勒公式，有

其中_η2在x与X₁之间.由此可知，存在X>X₁，当x≥X时，f（x）>0.若取ξ=X，则f（ξ）f′（ξ）f″（ξ）f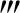（ξ）>0.