如何证明函数在区间上的一致连续性？

1.函数f（x）在区间I上一致连续是指：∀ε>0，∃δ>0，∀x₁，x₂∈I，只要∣x₁-x₂∣<δ，就有∣f（x₁）-f（x₂）∣<ε.其本质是说f（x）在区间I上的变化是相对均匀的.

证明函数f（x）在区间I上一致连续常用的方法：1）用定义；2）利普希茨（Lips-chitz）条件；3）导函数有界.若I=[a，b]，只需要证明f（x）在[a，b]上连续即可.

一致连续函数的运算性质与连续函数不尽相同，请注意以下各命题与连续函数相应命题的异同.

（1）设f（x）与g（x）在区间I上一致连续，则f（x）±g（x）在I上也一致连续；

（2）设f（x）与g（x）在R上一致连续且有界，则f（x）g（x）在R上也一致连续且有界（在无限区间上一致连续的函数未必有界，如：f（x）=x）；

（3）若f（x）与g（x）在有限区间I上一致连续，则f（x）g（x）也在I上一致连续（易证有限区间上的一致连续函数必有界）；

（4）若f（x）在区间I（有限或无限）上一致连续，且有正的下确界（或负的上确界），则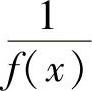在I上也一致连续；

（5）设f（u）在区间U上一致连续，g（x）在区间I上一致连续且g（I）⊂U，则复合函数f·g（x）在区间I上也一致连续.

需要特别注意的是，连续函数的反函数的连续性定理，对一致连续性未必成立.例如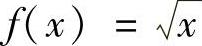，在（0，+∞）上一致连续，而它的反函数f^-1（x）=x²在（0，+∞）上却不一致连续.但对有限区间而言，结论仍成立.

2.证明函数f（x）在区间I上不一致连续，常用的方法：

1）用定义，即证∃ε₀>0，∀δ>0，∃x′，x″∈I，尽管∣x′_-x″∣<δ，但∣f（x′）-f（x″）∣≥ε₀；

2）用序列法，即证：∃I上的两个序列{x′_n}，{x″_n}，尽管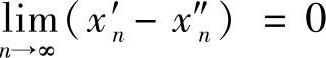，但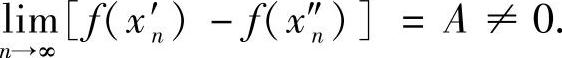

首先，我们给出f（x）在区间I上一致连续的几个充要条件，其结论可作为一致连续的判别法则使用.

例2.22 证明：设f（x）在有限区间（a，b）上连续，则f（x）在（a，b）上一致连续的充要条件是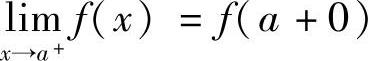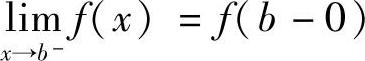：，都存在且有限（山东大学，南开大学）.

证明 （⇐）.定义函数

则F（x）在闭区间[a，b]上连续.由康托（Cantor）定理，F（x）在[a，b]上一致连续.显然，对于一致连续函数，当定义域缩小时，其一致连续性仍然保持.于是F（x）在开区间（a，b）上也一致连续，从而f（x）在（a，b）上一致连续.

（⇒）.若f（x）在（a，b）上一致连续，则∀ε>0，∃δ>0（0<δ<b-a），∀x′，x″∈（a，b），只要x′-x″<δ，就有

∣f（x′）-f（x″）∣<ε.

将x′，x″取在（a，a+δ）或（b-δ，b）内，由柯西收敛准则可知，lim

x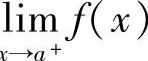与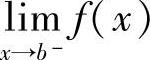存在且有限.

注2.2 若（a，b）是无限区间，则本例的条件是f（x）在（a，b）上一致连续的充分条件，但不必要.例如，f（x）=x，g（x）=sinx都在（-∞，+∞）上一致连续，但f（-∞）=-∞，f（+∞）=+∞，而g（-∞），g（+∞）均不存在.

对无限区间，其充分性的证明如下：

设f（-∞）与f（+∞）存在且有限，f（x）在（-∞，+∞）上连续，则由柯西收敛准则，∀ε>0，∃M>0，当x′，x″>M或x′，x″<-M时，都有

f（x′）-f（x″）<ε.（1）

由于f（x）在[-M-1，M+1]上连续，所以一致连续，故对上述ε>0，∃δ₁>，∀x′，x″∈[-M-1，M+1]，只要∣x′_-x″∣<δ₁，也有式（1）成立.

取δ=min{δ₁，1}>0，则∀x′，x″∈（-∞，+∞）及∣x′-x″∣<δ，总有式（1）成立，从而f（x）在（-∞，+∞）内一致连续.

类题 若f（x）在[a，+∞）上连续，且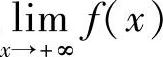存在.问：f（x）在[a，+∞）上是否有界？是否能取到最大、最小值？是否一致连续？

提示 第一、第二问参见例2.9，第三问参见注2.2.

例2.23 证明：函数f（x）在区间I上一致连续的充要条件是：∀{x_n′}，{x″_n}⊂I，只要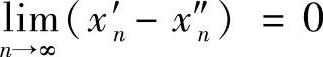，就有.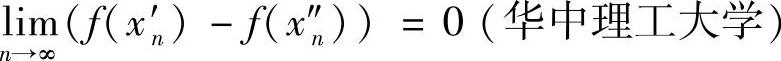

证明 （⇒）.因为f（x）在I上一致连续，所以∀ε>0，∃δ>0，∀x′，x″∈I，只要∣x′-x″∣<δ，就有∣f（x′）-f（x″）∣<ε.

对上述δ>0，由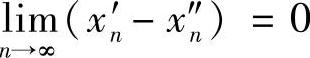可知，∃N>0，当n>N时，有x′_n-x″_n<δ，从而∣f（x′_n）-f（x″_n）∣<ε，此即为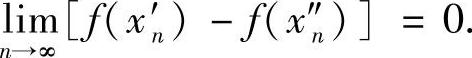

（⇐）.用反证法.函数f（x）在I上不一致连续可表述为：∃ε₀>0，∀δ>0，∃x′，x″∈I，尽管∣x′_-x″∣<δ，但∣f（x′）-f（x″）∣≥ε₀.

取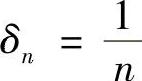，n=1，2，…，相应地存在x′_n，x″_n∈I，满足

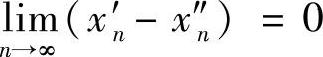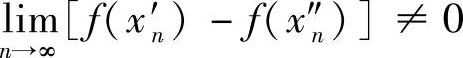显然，，但，矛盾.

注2.3 这个例题的结论，为判断函数在区间I上不一致连续提供了便利的方

法.例如，证明：f（x）=lnx在（0，+∞）上不一致连续.

取x′_n=e^-（n+1），x″_n=e^-n，n=1，2，…则有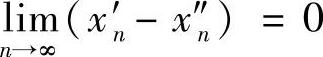， 但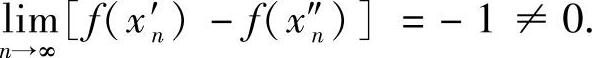

由此可知，f（x）=lnx在（0，+∞）上不一致连续.

类题 证明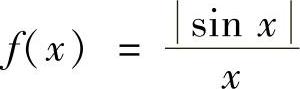：在（-1，0）和（0，1）上一致连续，但是在0<x<1上并非一致连续.

提示 f（x）在（-1，0）和（0，1）上的一致连续性，利用例2.20易证.至于f（x）在0<∣x∣<1上的非一致连续性，可取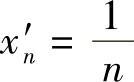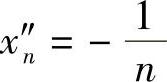，，n=2，3，…，显然

但

例2.24 定义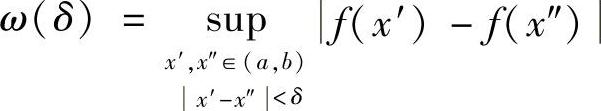，称ω（δ）为f（x）在（a，b）上的连续模.证明：f（x）在（a，b）上一致连续的充要条件是：

证明 （⇐）.若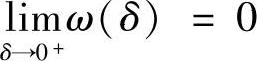，则∀ε>0，∃δ₁>0，当0<δ<δ₁时，有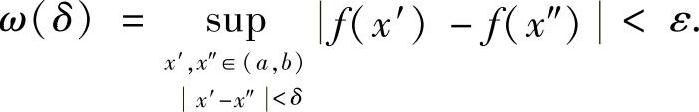于是，∀x′，x″∈（a，b），只要∣x′-x″∣<δ<δ₁，便有∣f（x′）-f（x″）∣<ε，即f（x）在（a，b）上一致连续.

（⇒）显然.

类题 设f（x）在[a，b]上连续，证明：存在函数ψ（x），在（0，+∞）上具有下述性质：

1）ψ（x）在（0，+∞）上单调上升，当x≥b-a时，ψ（x）为常数；

2）∀x′，x″∈[a，b]，有∣f（x′）-f（x″）∣≤ψ（∣x′-x″∣）；

3）

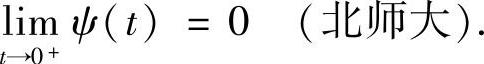
提示 根据连续模的性质，可定义ψ（x）如下：

其中，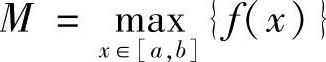

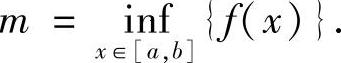
当x₂>x₁>0时，显然ω（x₁）≤ω（x₂），故ψ（x）具有性质1）.

由上确界的性质，易知ψ（x）具有性质2）.

由f在[a，b]上的一致连续性及例2.24知，ψ（x）具有性质3）.

注2.4 利用连续模的估值ω（δ）≤Mδ^r可求出一致连续定义中所需要的δ（ε）.例如，f（x）=x³，x∈（0，1），则∀x，y∈（0，1），当∣x-y∣<δ时，有

ω（δ）=sup∣x³-y³∣=sup∣x-y∣·∣x²+xy+y²∣

≤3sup∣x-y∣≤3δ.

由此可见，∀ε>0，取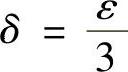即可.

例2.25f（x）在有界实数集E上一致连续的充要条件是：f把E中的柯西列变为R中的柯西列.

证明 （⇒）.若f在E上一致连续，则∀ε>0，∃δ>0，∀x′，x″∈E，只要∣x′-x″∣<δ，就有∣f（x′）-f（x″）∣<ε.

设{x_n}是E中任一柯西列，对上述δ>0，∃N>0，当n，m>N时，有∣x_n-x_m∣<δ，从而有∣f（x_n）-f（x_m）∣<ε.这表明{f（x_n）}是柯西列.

（⇐）假设f（x）在E上非一致连续，则∃ε₀>0，对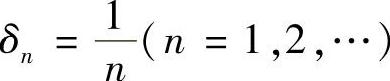，相应地存在x′_n和x″_n，尽管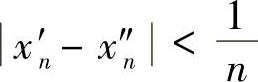，但

f（x′_n）-f（x″_n）∣≥ε0.

注意到{x′_n}是有界数列，由致密性定理，它存在收敛子列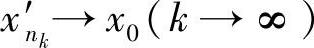.与此相对应的{x″_n}也有一个子列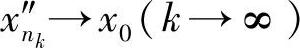.即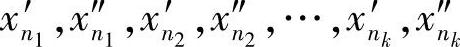，…是E中的柯西列，但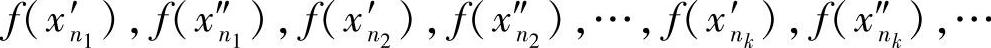却发散，不是柯西列.

注　必要性的证明没有用到E的有界性.

例2.26　按一致连续的定义论证：

（1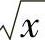）在[0，+∞）上一致连续；

（2）lnx在[1，+∞）上一致连续.

证明　（1）∀ε>0，取δ=ε²>0，∀x′，x″∈[0，+∞），当∣x′_-x″∣<δ时，分两种情形讨论.

1）当max{x′，x″}≥ε²时，有

2）当max{x′，x″}<ε²时，不妨设x′≥x″，则有

所以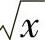在[0，+∞）上一致连续.

（2）我们将会用到一个熟知的不等式：

ln（1+x）≤x　（x≥0）. （1）

∀ε>0，取δ=ε>0，∀x′，x″∈[1，+∞），当∣x′-x″∣<δ时，（不妨设x′≥x″），有

所以lnx在[1，+∞）上一致连续.

例2.27　设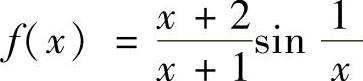，a>0为正常数.试证：f（x）在（0，a）内非一致连续，在[a，+∞）上一致连续（兰大）.

证明　（1）证明f在（0，a）内非一致连续.

取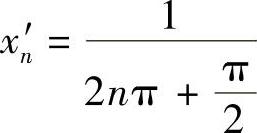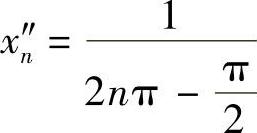，，n=1，2，…，则当n充分大时，x_n′，x_n″∈（0，a），(www.xing528.com)

且

但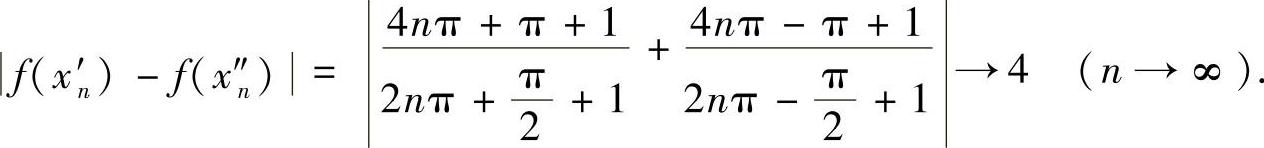

故f在（0，a）内非一致连续.

（2）证明f在[a，+∞）上一致连续.

只要证明f′（x）在[a，+∞）上有界即可.事实上，

类题 证明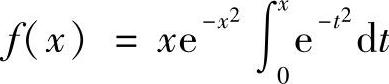：在[0，+∞）上一致连续.

提示 只需证明f′（x）在[0，+∞）上有界即可，为此只需证明存在且有限即可.

例2.28 若周期函数f（x）在（-∞，+∞）上连续，证明：

（1）f（x）在（-∞，+∞）上一致连续；

（2）f（x）=sin²x+sinx²不是周期函数.

证明 （1）设T为f（x）的周期，则f（x）在[0，2T]上一致连续，即∀ε>0，∃δ>0，∀x′，x″∈[0，2T]，只要∣x′_-x″∣<δ，就有

f（x′）-f（x″）<ε.

∀x′，x″∈R，满足∣x′_-x″∣<δ<T，则必存在整数m，使x′=mT+t′，x″=mT+t″，且min{t′，t″}∈[0，T].于是，t′，t″∈[0，2T]且满足∣t′_-t″∣≤∣x′-x″∣<δ，故f（x′）-f（x″）=f（t′）-f（t″）<ε.这就证明了f（x）在R上一致连续.

（2）f（x）在（-∞，+∞）上连续显然.若f（x）是周期函数，由（1）知，f（x）在（-∞，+∞）上必一致连续，所以只要证明f（x）在（-∞，+∞）上不一致连续即可.

事实上，取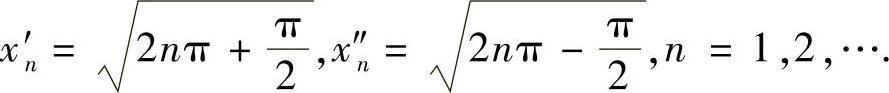尽管

但f∣（x′_n）-f（x″_n）∣=∣sin²x′_n-sin²x″_n+2∣→2≠0 （n→∞），故f（x）在（-∞，+∞）上不一致连续.

这里应用了

例2.29 设λ为正实数，确定使x^λ在[0，+∞）上一致连续的λ的范围以及使x^λ在[0，+∞）上不一致连续的λ的范围（要叙述过程）（川大）.

解 当λ=1时，x显然在[0，+∞）上一致连续.

下证：当0<λ<1时，x^λ在[0，+∞）上一致连续；当λ>1时，x^λ在[0，+∞）上不一致连续.

事实上，当0<λ<1时，因为x^λ在[0，1]上一致连续，所以只要证明它在[1，+∞）上一致连续即可.由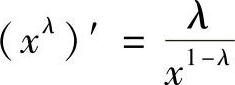在[1，+∞）上有界可知，x^λ在[1，+∞）上一致连续.

当λ>1时，取x′_n=n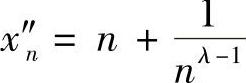，，尽管

但是

故x^λ在[0，+∞）上不一致连续.

从例2.27可以看出，幂函数要想在无限区间上一致连续，当x充分大时，其增长的阶数不超过1阶.对一般的函数也有同样的结论，请看下面的例题.

例2.30 设f（x）在（-∞，+∞）上一致连续，则存在非负实数a和b，使∀x∈（-∞，+∞），都有

f（x）≤ax+b.

试证明之（云南大学；南开大学）.

证明 因为f（x）一致连续，所以∀ε>0，∃δ>0，∀x′，x″∈（-∞，+∞），只要∣x′-x″∣≤δ，就有∣f（x′）-f（x″）∣<ε.

现将ε>0，δ>0固定.由于∀x∈（-∞，+∞），存在整数n，使得x=nδ+x₀，其中x₀∈（-δ，δ）.注意到f（x）在[-δ，δ]上有界，即∃M>0，使得∣f（x）∣≤M.因此，

由x=nδ+x₀知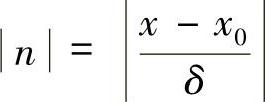，，代入上式，有

记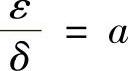，M+ε=b，则a>0，b>0，使

∣f（x）∣≤a∣x∣+b，∀x∈（-∞，+∞）.

类题 设函数f（x）在开区间（1，+∞）上一致连续.证明：

（1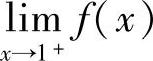）存在且有限；

（2）函数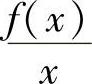在（1，+∞）上有界（南开大学）.

提示 （1）参见例2.22必要性的证明；

（2）重复例2.30的证明可得：∃a，b≥0，使f（x）≤ax+b.由此可得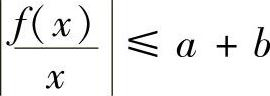，有界.

例2.31 设f（x）在[a，+∞）（a>0）上满足利普希茨条件，

∣f（x）-f（y）∣≤k∣x-y∣，∀x，y∈[a，+∞）.

证明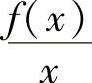：在[a，+∞）上一致连续.

证明 只要证明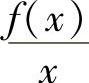在[a，+∞）上满足利普希茨条件即可.∀x∈[a，+∞），由∣f（x）-f（a）∣≤k∣x-a∣可得

∣f（x）∣≤∣f（a）∣+k∣x-a∣.

∀x，y∈[a，+∞），考察

这表明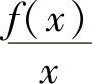在[a，+∞）上也满足利普希茨条件.

例2.32 设f（x）在[a，+∞）上连续，当x→+∞时，y=cx（c为常数）为f（x）的渐近线，证明：f（x）在[a，+∞）上一致连续.

证法1 令F（x）=f（x）-cx，则F（x）在[a，+∞）上连续，且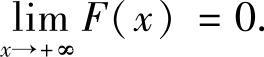由注2.2，F（x）在[a，+∞）上一致连续.而y=cx显然在[a，+∞）上一致连续，故f（x）=F（x）+y在[a，+∞）上一致连续.

证法2 直接证明.由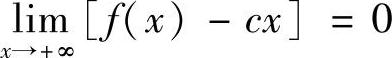，∀ε>0，∃M>0，当x≥M时，有∣f（x）-cx∣<ε/3.

于是，取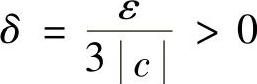，∀x′，x″>M，且∣x′_-x″∣<δ，有

即f（x）在[M，+∞）上一致连续.而f（x）显然在[a，M+1]上一致连续，故f（x）在[a，+∞）上一致连续.

例2.33 设φ（x）在R上连续，且

证明：（1）若n为奇数，则存在x，满足xⁿ+φ（x）=0；

（2）若n为偶数，则存在y，使得∀x，有

yⁿ+φ（y）≤xⁿ+φ（x）.

证明 （1）当n为奇数时，∃b>0，使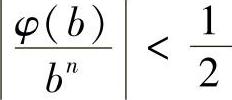，故

同时存在a<0，使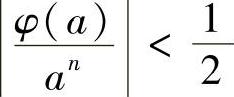，故

对xⁿ+φ（x）在[a，b]上应用根的存在定理即可.

（2）当n为偶数时，则∃c>0，满足cⁿ>2φ（0），即当∣x∣>c时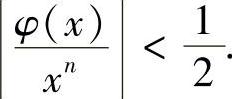，故当∣x∣>c时，

取a>c，当x>a时，仍有xⁿ+φ（x）>φ（0），所以xⁿ+φ（x）在R上的最小值必在[-a，a]内取到.设在y点取到，则∀x∈R，有yⁿ+φ（y）≤xⁿ+φ（x）.

最后，我们看一个使用一致连续性的例子.

例2.34　设函数f（x）在[0，+∞）上一致连续，且

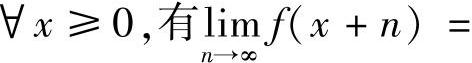0（n为正整数）.试证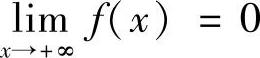：（江西大学；上海师大；中科院计算中心）.

证明　因为f（x）在[0，+∞）上一致连续，所以∀ε>0，∃δ>0，∀x′，x″∈[0，+∞），只要x′-x″<δ，就有

对固定的δ>0，取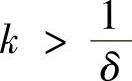且为正整数，将[0，1]区间k等分.记分点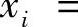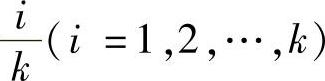，则每个小区间的长度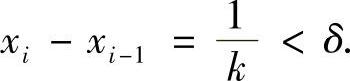

由已知条件，对每个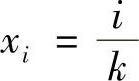，有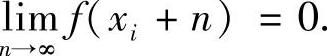故对上述ε>0，∃N_i>0，当n>N_i时，有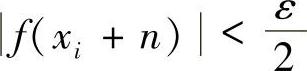.令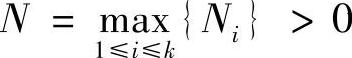，则当n>N时，有

∀x>N，记n=[x]≥N，因为x-n∈[0，1），故∃i∈{1，2，…，k}，使得∣（x-n）-x_i∣<δ，即∣x-（n+x_i）∣<δ，由式（1），有

再由式（2），有

∣f（x）∣≤∣f（x）-f（n+x_i）∣+∣f（n+x_i）∣

即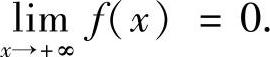

本题亦可用反证法予以证明.

事实上，若结论不对，则存在∃ε₀>0，对∀n∈N+，相应地存在x_n>n，使得f（x_n）∣>ε_0.

记y_n=x_n-[x_n]，则0≤y_n<1.由{y_n}的有界性知，它存在一个收敛子列，不妨设为它本身，满足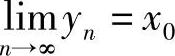，或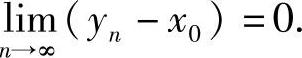

由f（x）在[0，+∞）上一致连续可知，对上述ε₀>0，∃δ₀>0，∀x，y∈[0，+∞），只要∣x-y∣<δ₀，就有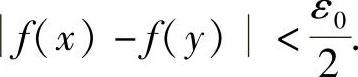于是，当n充分大时，有

∣（[x_n]+x₀）-（[x_n]+y_n）∣=∣y_n-x₀∣<δ₀，

从而有

由此可得

这与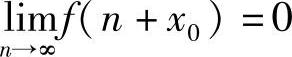的假设矛盾.