【摘要】:为方便起见,我们不加证明地将施图兹定理叙述如下:施图兹定理设{yn}是严格单调增加的正无穷大量,且,则注1.3 施图兹定理在处理一类复杂数列的极限时,非常方便!).且由知,{xn}↓.由单调有界定理,存在,易知x=0.由施图兹定理,
为方便起见,我们不加证明地将施图兹定理叙述如下:
施图兹定理 设{yn}是严格单调增加的正无穷大量,且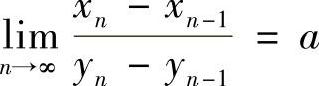 (a可为有限量,也可为+∞或-∞),
(a可为有限量,也可为+∞或-∞),
则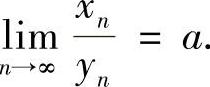
注1.3 施图兹定理在处理一类复杂数列的极限时,非常方便!
例如,在例1.1(1)中,若令xn=a1+a2+…+an,yn=n,可立即得到结论.
例1.17 求极限
解 令xn=1k+2k+…+nk,yn=nk+1,由
可得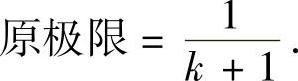
注1.4 本例也可用定积分的定义求解.
事实上,取f(x)=xk,将和式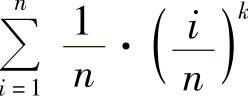 看做是f(x)在[0,1]上相应于n等分的积分和即可,即
看做是f(x)在[0,1]上相应于n等分的积分和即可,即
由此可以看出,用定积分定义求解本例,不要求k为自然数,只要求k>0即可.
例1.18 设α∈R,求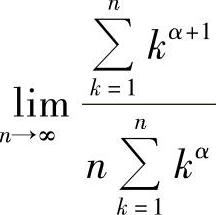 .
.
解 记 .由施图兹定理,
.由施图兹定理,
类题 设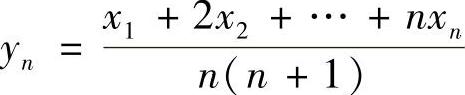 ,若
,若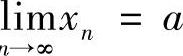 ,证明:(https://www.xing528.com)
,证明:(https://www.xing528.com)
(1)当a为有限数时,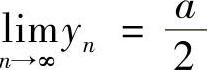 ;(2)当a=+∞时,
;(2)当a=+∞时, (上海大学).
(上海大学).
例1.19 对于数列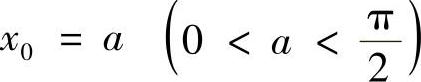 ,xn=sinxn-1(n=1,2,…).
,xn=sinxn-1(n=1,2,…).
证明 (1) ;(2)
;(2)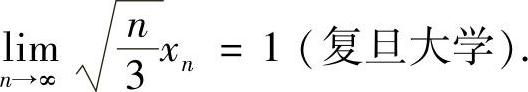
证明 (1)由不等式0<sinx<x 知,{xn}单调递减且有下界0.由单调有界定理,
知,{xn}单调递减且有下界0.由单调有界定理, 存在.若记为ξ,则
存在.若记为ξ,则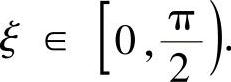 在等式xn=sinxn-1两边取极限可得ξ=sinξ.注意到ξ的范围知ξ=0,即lim n
在等式xn=sinxn-1两边取极限可得ξ=sinξ.注意到ξ的范围知ξ=0,即lim n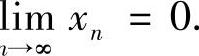
(2)考虑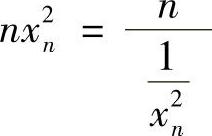 .分母单调趋向于+∞,由施图兹定理,
.分母单调趋向于+∞,由施图兹定理,
上式右端是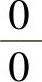 型的不定式,将其换成连续变量t,使用洛必达法则,有
型的不定式,将其换成连续变量t,使用洛必达法则,有
再由海涅定理知,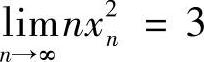 ,即
,即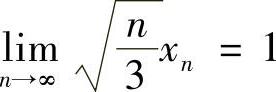 .
.
类题1 设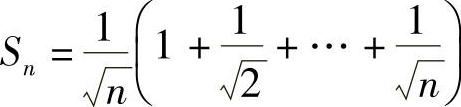 ,求
,求 .
.
答案 2.
类题2 设0<x1<1,xn+1=xn(1-xn),n=1,2,….证明:
提示(1) ,即
,即 (n=2,3,…).且由
(n=2,3,…).且由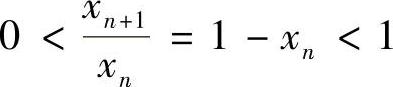 知,{xn}↓.由单调有界定理,
知,{xn}↓.由单调有界定理,
 存在,易知x=0.
存在,易知x=0.
(2)由施图兹定理,
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




