柯西收敛准则证明极限存在性

例1.15　方程x=m+εsinx　（0<ε<1）称为开普勒方程.若x₀=m，x₁=m+εsinx₀，…，x_n=m+εsinx_n-1，…，则数列{x_n}收敛.设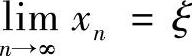，则ξ是开普勒方程的唯一解（即ξ=m+εsinξ），亦称为方程的不动点（复旦大学）.

证明 考察

于是，对任意的自然数p，有

由柯西收敛准则，{x_n}收敛.若设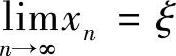，在方程x_n=m+εsinx_n-1两边取极限可知，ξ是开普勒方程的解，即ξ=m+εsinξ.

下证：唯一性.

若_η也是开普勒方程的解，即η=m+εsinη，则

∣ξ-η∣=ε∣sinξ-sinη∣≤ε∣ξ-η∣，

由0<ε<1知，∣ξ-η=∣0，即ξ=η.这表明ξ是开普勒方程的唯一解.

例1.16 用柯西收敛准则证明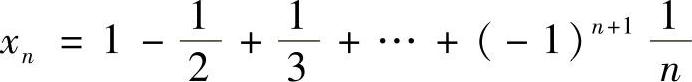：收敛.

证明 当n适当大时，对任意的自然数p，有(www.xing528.com)

∀ε>0，取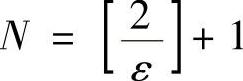，当n>N时，∀p为自然数，都有

|x_n+p-x_n|<ε.

由柯西收敛准则，{x_n}收敛.

类题1 用柯西收敛准则证明下列数列发散.

提示 “数列{x_n}不满足柯西收敛准则”的正面陈述是：∃ε₀>0，∀N>0，∃n₀，m₀≥N，使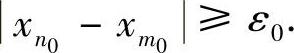

（1）取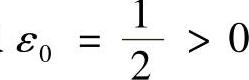，∀N>0，取n₀=2N，m₀=N，则有

（2）用不等式lnx<x（x>1）易证.

类题2 判断题：数列{a_n}收敛的充要条件是：∀ε>0，∃N>0，使得当n>N时，恒有∣a_2n-a_n∣<ε.（正确的说明理由，错误的举出反例）（华东师大）

提示 该论断不正确.考察数列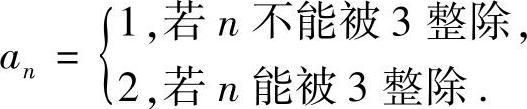：不难发现，{a_n}满足：∀ε>0，∃N>0，当n>N时，恒有∣a_2n-a_n∣<ε，但数列{a_n}不收敛.