例1.10 证明: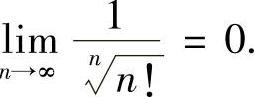
证明 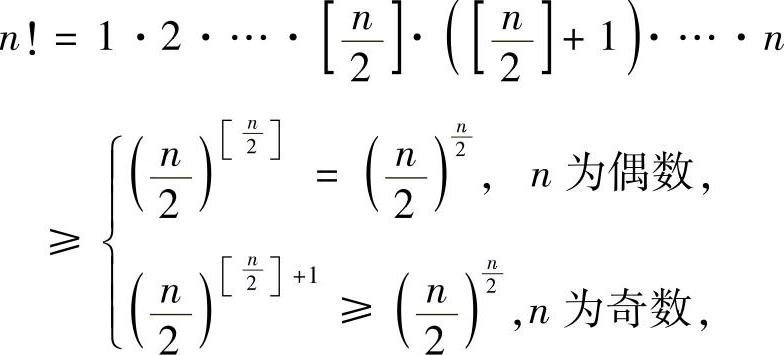
故 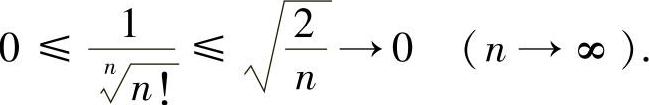
例1.11 设a1,b1为任意选定的实数,an和bn的定义为:
试证: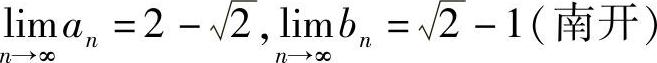 .
.
证明 先证明{an},{bn}是有界数列.当n=2,3,…时,有
于是,当n=3,4,…时,有
由此可见,当n≥3时,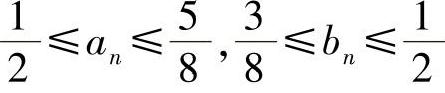 ,即{an},{bn}有界.
,即{an},{bn}有界.
再给出{an},{bn}的递推关系式.当n≥3时,有
从式(1)、式(2)中消去bn,可得:
最后研究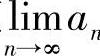 ,
,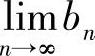 的存在性.
的存在性.
记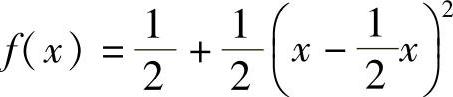 ,
,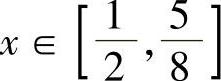 ,则
,则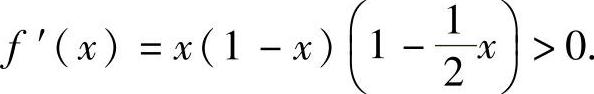
由此可知,无论a2≥a4,还是a2≤a4,数列{a2n}均单调有界,因而极限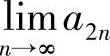 存在,记为A1.
存在,记为A1.
同理可以证明,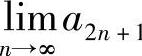 也存在,记为A2.
也存在,记为A2.
由式(3)可知,A1,A2应该是方程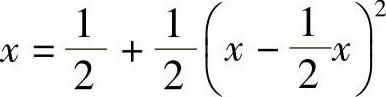 在
在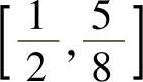 上的两个实根.注意到
上的两个实根.注意到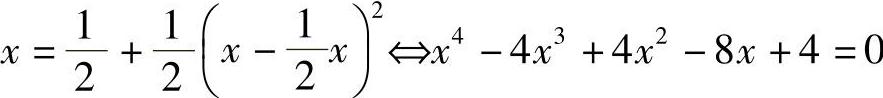 ,而
,而
所以,方程x4-4x3+4x2-8x+4=0在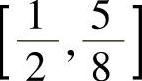 上的实根,就是方程x2-4x+2=0
上的实根,就是方程x2-4x+2=0
在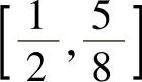 上的唯一实根
上的唯一实根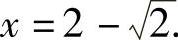 这表明
这表明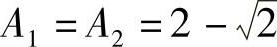 ,从而
,从而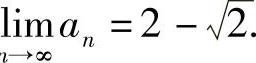
再由式(2)可知,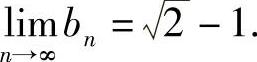
例1.12 设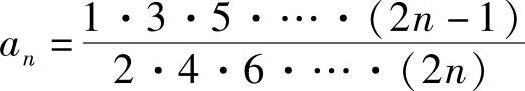 ,(1)求
,(1)求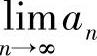 ;(2)求
;(2)求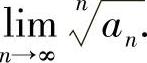
解 (1)由于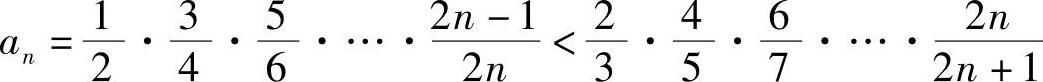 ,所以
,所以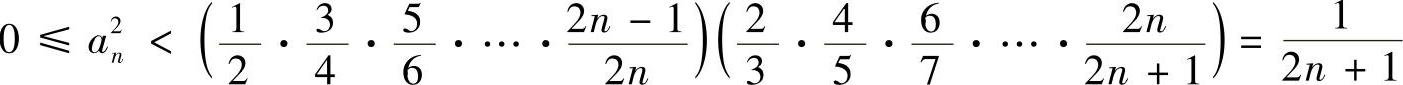 ,
,
故
(2)一方面,由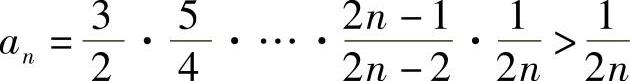 ,可得
,可得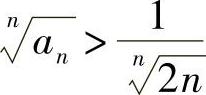 ;另一方面,由式(1)可知,
;另一方面,由式(1)可知,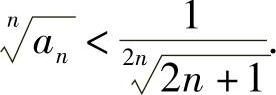 联合以上两式,有
联合以上两式,有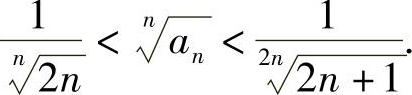 由迫敛性定理,
由迫敛性定理,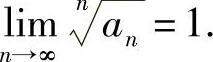
例1.13 求极限 (数学Ⅲ).
(数学Ⅲ).
解 记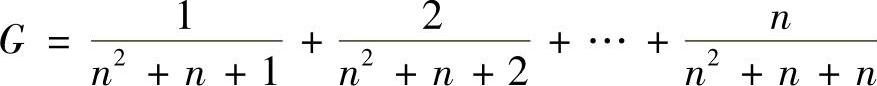 ,则
,则
即 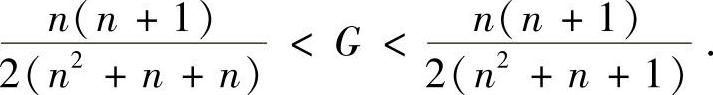 (https://www.xing528.com)
(https://www.xing528.com)
而 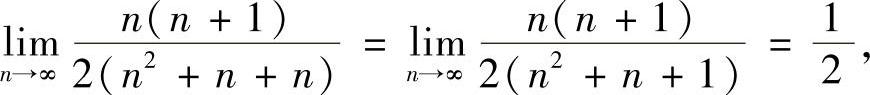
故 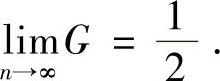
类题1 求下列极限
提示 (1)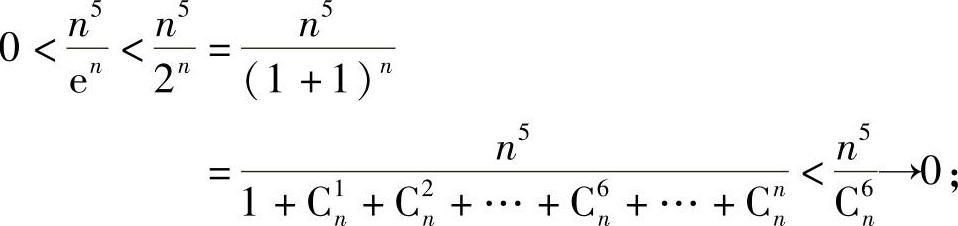
(2)因为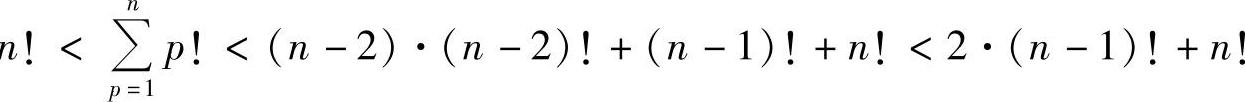 ,
,
所以 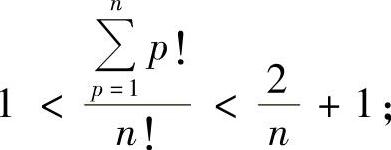
(3)因为α-1<0,所以(1+n)α-1<nα-1,故(1+n)α<nα-1(1+n)=nα+nα-1,即0<(1+n)α-nα<nα-1→0.
类题2 (1)若a1,a2,…,am为m个正数,证明:
(2)求极限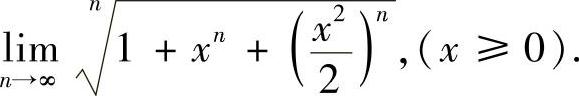
提示 (1)记G=max{a1,a2,…,am},则
由迫敛性定理可得结论;
(2)由(1),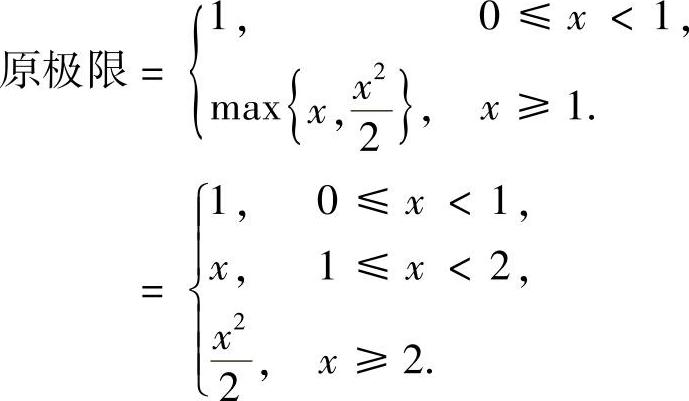
类题3 设Φn满足: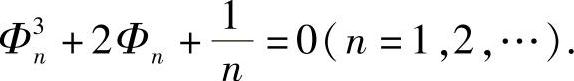 求
求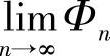 (解放军信息工程大学).
(解放军信息工程大学).
提示 由已知条件,有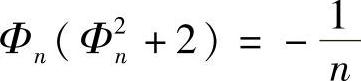 ,n=1,2,….由此可知,Φn<0,即{Φn}有上界.
,n=1,2,….由此可知,Φn<0,即{Φn}有上界.
再由已知条件,可得
由此可知,{Φn}单调递增,故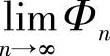 存在,记为φ,在所给的等式两边取极限可得:φ3+2φ=0.由{Φn}的递增性知φ=0.
存在,记为φ,在所给的等式两边取极限可得:φ3+2φ=0.由{Φn}的递增性知φ=0.
例1.14 设a1>b1>0,且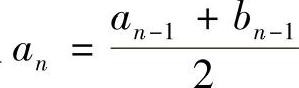 ,
,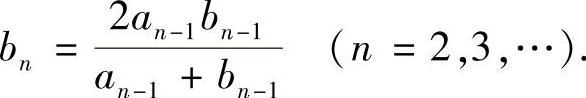 证明数列{an}、{bn}的极限存在且都等于
证明数列{an}、{bn}的极限存在且都等于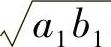 (北师大).
(北师大).
证明 显然,an,bn>0且
由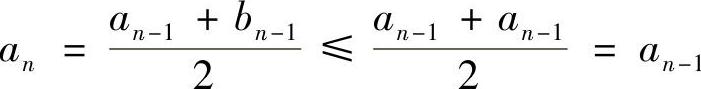 知,{an}↓;由
知,{an}↓;由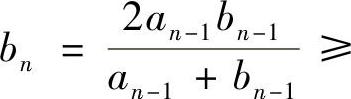
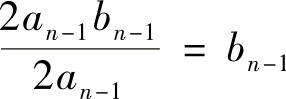 知,{bn}↑.
知,{bn}↑.
又由an≥bn≥bn-1≥…≥b1知,{an}有下界,
bn≤an≤an-1≤…≤a1知,{bn}有上界.
由单调有界定理,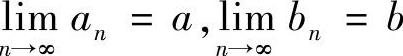 都存在.在
都存在.在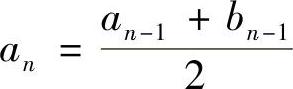 两边取极限可得,a=b.
两边取极限可得,a=b.
再由anbn=an-1bn-1可推知anbn=a1b1,取极限可得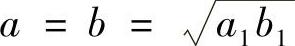 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




