例1.4 证明数列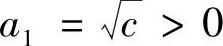 ,
,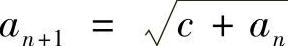 的极限存在,并求其值.
的极限存在,并求其值.
证明 显然{an}↑,下证{an}有上界.
设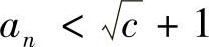 ,则
,则
即{an}有上界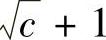 .
.
由单调有界定理,{an}的极限存在,设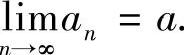 在a2n+1=c+an中,令n→∞得a2=c+a,解之,得
在a2n+1=c+an中,令n→∞得a2=c+a,解之,得
例1.5 若{an}↑,{bn}↓,且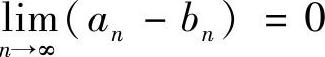 ,证明
,证明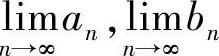 都存在,并且相等(南京航空航天大学).
都存在,并且相等(南京航空航天大学).
证明 由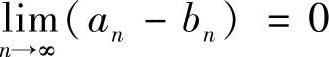 知,∃N0>0,当n≥N0时,有
知,∃N0>0,当n≥N0时,有
-1<an-bn<1.
由此知,an<bn+1≤bn-1+1≤…≤bN0+1,即{an}有上界;
bn>an-1≥an-1-1≥…≥aN0-1,即{bn}有下界.
由单调有界定理,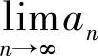 ,
,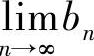 都存在.由
都存在.由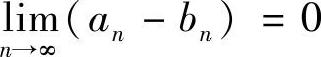 可得:
可得: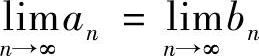 ,即两者极限相等.
,即两者极限相等.
例1.6 设{an},{bn}均为正整数数列,a1=b1=1,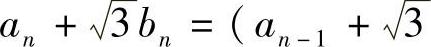
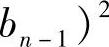 .证明:数列
.证明:数列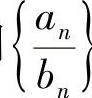 的极限存在,并求该极限值(南开).
的极限存在,并求该极限值(南开).
解 当n≥2时,由{an},{bn}均为正整数数列,利用已知的递推关系式可得
an=a2n-1+3b2n-1, bn=2an-1bn-1,
进而有 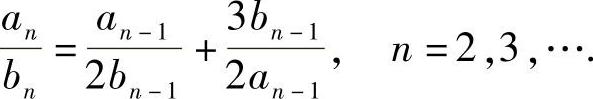
记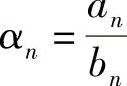 ,则上式可化为
,则上式可化为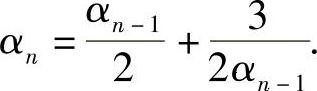 由此易得
由此易得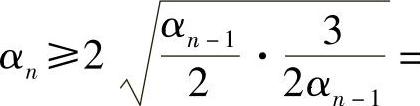
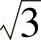 ,这表明数列{αn}有下界.
,这表明数列{αn}有下界.
例1.7 设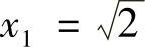 ,
,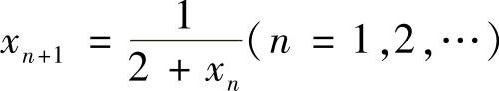 .证明数列{xn}收敛,并求其极限.
.证明数列{xn}收敛,并求其极限.
证法1 假设{xn}的极限存在,并设为A,则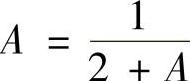 ,即A2+2A-1=0,
,即A2+2A-1=0,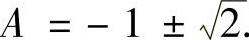 因为xn>0,故
因为xn>0,故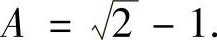
若xn<A,则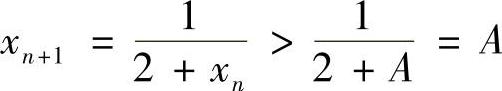 ;
;
若xn>A,则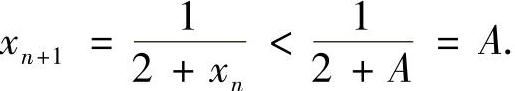
由 知,x2n+1>A,而x2n<A.
知,x2n+1>A,而x2n<A.
下面将证明:{x2n+1}↓A,{x2n}↑A.事实上,
而1-2x-x2=0的根为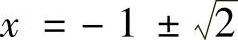 ,故
,故
即{x2n}↑以A为上界,{x2n+1}↓以A为下界,故它们的极限都存在,分别设为α,β.由
取极限可得
故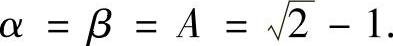
类题 设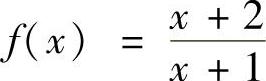 ,数列{xn}由如下递推公式定义:x0=1,xn+1=f(xn)(n=0,1,2,…),求证
,数列{xn}由如下递推公式定义:x0=1,xn+1=f(xn)(n=0,1,2,…),求证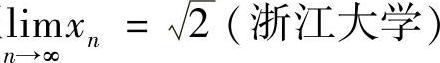 .
.
注1.2 下面介绍一个有用的命题.设数列{xn}满足压缩性条件:
∣xn+1-xn∣≤k∣xn-xn-1∣(0<k<1; n=2,3,…),
则{xn}收敛.
这个命题的证明,用柯西收敛准则不难得到.
证法2 注意到xn>0,我们有
由命题知,
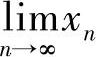 存在,在已知的等式
存在,在已知的等式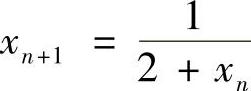 两边取极限,舍去负值,可得
两边取极限,舍去负值,可得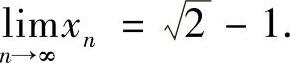
例1.8 设c>0,x1=a>0,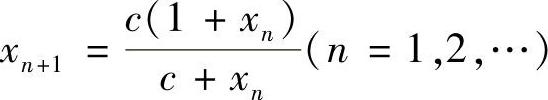 ,证明:
,证明: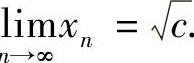
证明 由
利用已知的关系式xn(c+xn-1)=c(1+xn-1)可得
注意到xn≥0,由上式得
易见,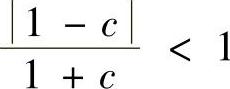 ,由命题知,
,由命题知,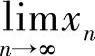 存在.在已知的关系式两边取极限可知
存在.在已知的关系式两边取极限可知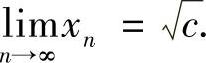
简单推论 设c>0,x1=a>0,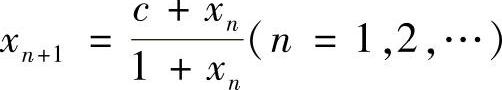 ,则
,则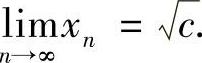 (https://www.xing528.com)
(https://www.xing528.com)
证明 令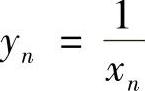 ,则有
,则有
由例1.8知,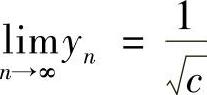 ,从而
,从而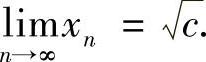
类题1 设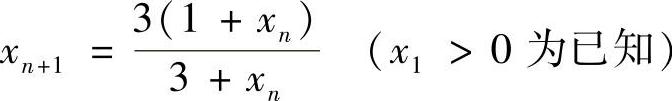 ,求
,求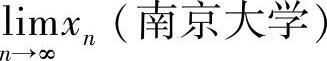 .
.
类题2 设a1=0,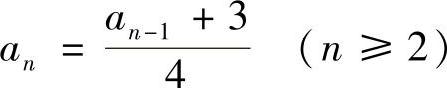 ,求
,求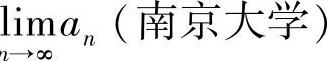 .
.
类题3 (斐波那契(Fibonacci)数列)设a0=a1>0,an+2=an+1+an(n=0,1,2,…),证明: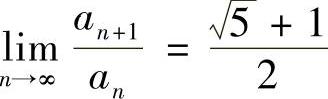 .
.
提示 令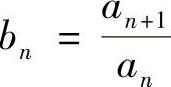 ,则有
,则有
由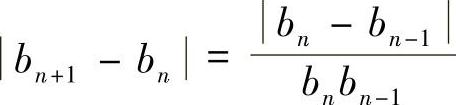 ,利用bnbn-1=bn-1+1可得
,利用bnbn-1=bn-1+1可得
又由bn>1可得
故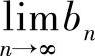 存在.
存在.
类题4 设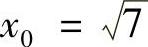 ,
, ,定义:
,定义:
证明:数列{xn}收敛并求其极限.
提示 设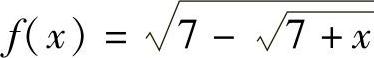 ,由拉格朗日中值定理,有
,由拉格朗日中值定理,有
f(x)-2=f(x)-f(2)=f′(ξ)(x-2),
其中,ξ在x与2之间.
由于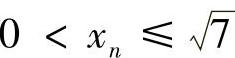 ,所以可限制
,所以可限制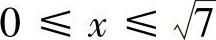 ,此时
,此时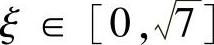 .于是,有
.于是,有
和 |xn+2-2|=|f(xn)-2|≤α|xn-2|,
故 |x2k-2|≤αk|x0-2|,|x2k+1-2|≤αk|x1-2|(k=1,2,…).
从而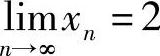 .
.
下面看一个与欧拉常数有关的数列.
例1.9 设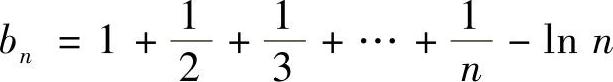 ,证明数列{bn}收敛(北师大).
,证明数列{bn}收敛(北师大).
证明 因为
所以 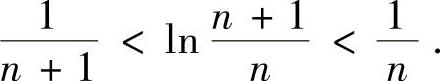
于是 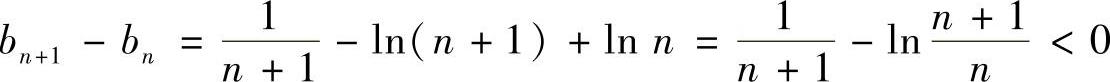 ,即{bn}单调递减.
,即{bn}单调递减.
又 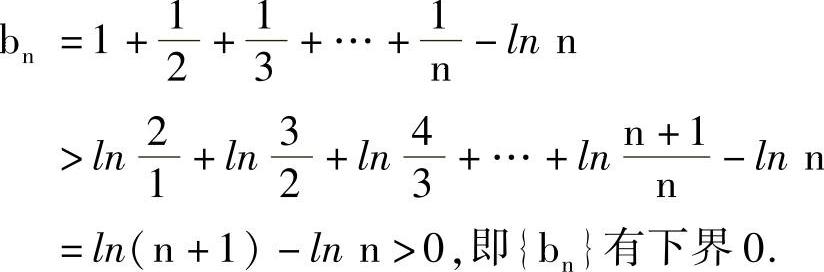
由单调有界定理,{bn}的极限存在,记为C(通常称为欧拉常数).
类题1 设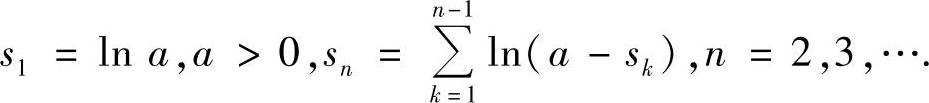
证明: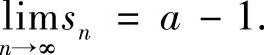
提示 利用不等式lnx≤x-1 (x>0),证明ln(a-sk)有意义.
当k=1时,a-s1=a-lna>0.
设k≤n时,有a-sk>0即ln(a-sk)有意义,于是,
sn+1-sn=ln(a-sn)≤a-sn-1,
所以sn+1≤a-1,即ln(a-sn+1)有意义且{sn}有上界.
由sn+1-sn=ln(a-sn)≥ln(a-(a-1))=0可知,{sn}↑.由单调有界定理,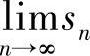 存在.易见
存在.易见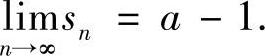
类题2 设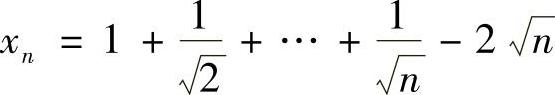 ,n=1,2,….证明:{xn}收敛.
,n=1,2,….证明:{xn}收敛.
提示 由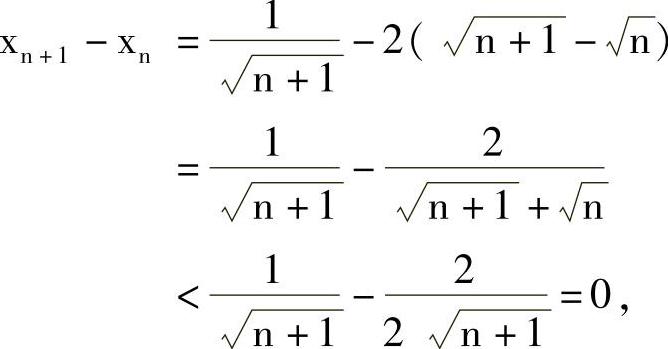 知{xn}↓.
知{xn}↓.
又由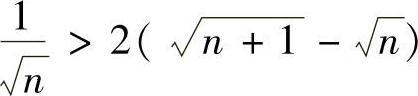 可得
可得
这表明{xn}有下界.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




