为了对云图像本文边缘提取算法的先进性进行验证,选择边缘特征比较明显的灰度图像进行测试,测试图像的尺寸为384×256。借助MATLAB7.0进行仿真分析,仿真条件为:Intel I5四核CPU,2.6GHz,4GB ROM,1TB硬盘,Win 7系统PC机。为了具有可比性,选择当前常用的图像边缘提取算法作为对照,分别为:文献[18]中改进的Canny边缘检测、文献[19]中基于蚁群优化的边缘检测和文献[20]中基于小波变换的边缘检测,分别记A、B、C算法。
(1)实验参数
参数对算法的性能具有重大的影响,因此,为了更好地体现本文算法的边缘提取的性能,通过多次试验得到了本文算法的最优参数,表示为:步长L=50,迭代次数N=4,区域半径r=4,权重因子α=6,β=0.01,初始信息数T0=0.0001,ρ=0.1,ξ=0.3,ε=0.01。
(2)实验结果与分析
图5-6为恐龙灰度图像通过三种对照组算法与本文算法提取的图像边缘结果。图5-6(a)为初始图,图5-6(b)-(e)分别为A、B、C与本文算法的结果。根据图5-6中的实验结果不难看出,四种算法对于无噪声图像得到的边缘都算比较完整,但是,A算法与B算法出现了一些细碎的边缘,C算法在尾部产生了一些断裂现象,而本文算法得到的边缘完整性较好,能够详细地反映图像的结构信息。本文的算法进行了边缘信息计算,通过计算图像像素的梯度和统计均值,并建立了二者之间的权重函数,准确地识别图像边缘。
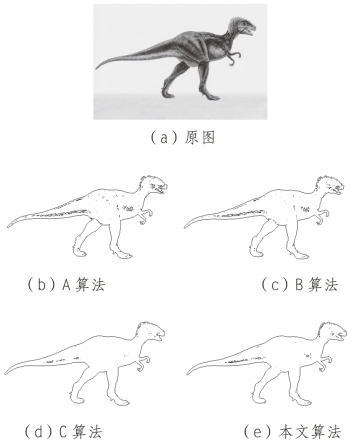
图5-6 无噪声图像边缘提取结果
为了体现算法的适应性和抗噪性,以图像中添加高斯噪声为例,如图5-7所示。图5-7为四种算法对含有均值为0,均方差为1的高斯噪声的实验结果。图5-8为四种算法对含有均值为0,均方差为5的高斯噪声的实验结果。图5-7(a)为含有均值为0均方差为1的钥匙灰度图像,图5-8(a)为含有均值为0均方差为5的钥匙灰度图像,图5-7和图5-8(b)-(e)分别为对照组与本文算法提取得到的边缘结果。依据图5-7看出,在高斯噪声均方差较小时,对提取的结果影响不大,说明四种算法在低噪声时能够较好的提取边缘,算法具有一定的抗噪性。根据图5-8看出,当噪声密度较大时,图5-8(b)中提取的结果中噪声比较明显,出现了较多的虚假边缘。图5-8(c)中由于噪声的存在,也出现了一些伪边缘,丢失了一些有用的边缘信息。图5-8(d)中算法能够一定程度上降低噪声的干扰,提高定位准确,但是得到的边缘出现小连续的现象。图5-8(e)为本文算法的结果,可看出其提取的边缘较完整,连续性好,大大降低了噪声的影响。主要原因是由于A算法采用WT与中值滤波代替高斯滤波,当噪声密度较大时,噪声像素很容易统计为弱边缘。而B算法通过线性加权将信息素、梯度值、支持区面积来计算蚂蚁经过某个点的概率,获得图像的边缘,但是容易导致变化缓慢的边缘丢失和提取虚假边缘。而C算法中虽然WT在边缘提取中可以降低噪声,但产生一些小连续边缘。
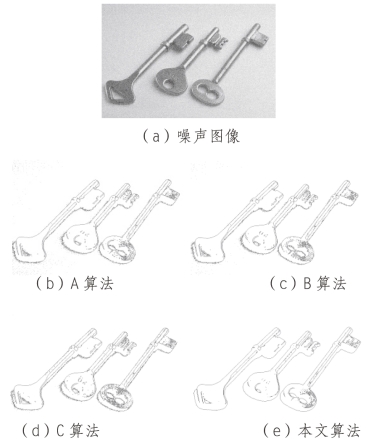
图5-7 低噪声密度图像边缘提取结果
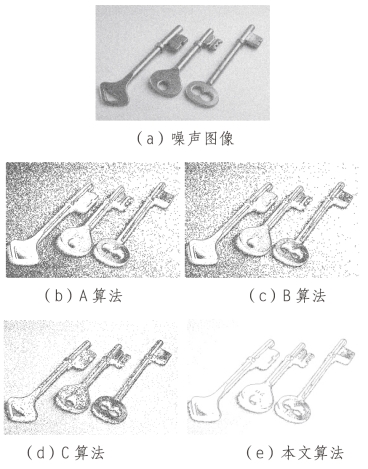
图5-8 高噪声密度图像边缘提取结果(https://www.xing528.com)
为了客观地对实验提取的边缘进行评价,引入优质系数Pz作为评价指标[21]。Pz的值越大,表明提取的边缘越完整,细节越详细,其定义如下:
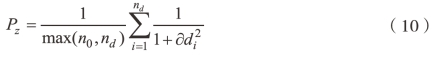
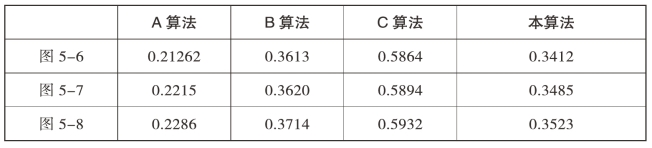
其中,n0和nd为完整与实际边缘上的像素点,di为第i点边缘与完整边缘的距离。表5-2分别为图5-6、图5-7和图5-8在四种算法下得到的优质系数值。表5-3为四种算法所消耗的时间结果。
表5-2 不同测试图像在不同算法下的Pr

续表

根据表5-2可得,在相同条件下,本算法得到的Pz在四种算法中最大,并且无噪声图像得到的值大于低噪声图像和高噪声图像,噪声密度越大,得到结果的Pz越小,说明提取的边缘质量越差,本算法中随着噪声的变化得到的Pz改变较少,都保持了较高的Pz值,说明其抗噪性较好。表5-3为四种算法时间消耗对比结果,本算法所消耗的比B算法和C算法低,稍微高于A算法。综合考虑,本算法具有较高的优质系数的同时花费的时间成本也较低。
表5-3 不同算法消耗的时间(单位:s)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




