【摘要】：5.判定矩阵是否可逆,若是可逆的,求A-1.
1.选择题.
(1)设A是一个三阶方阵,λ是一个实数,则下列各式成立的是( ).
A.det(λA)=λdetA B.det(λA)=|λ|detA
C.det(λA)=λ3detA D.det(λA)=|λ|3detA
(2)行列式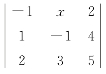
的展开式中x的系数为( ).
A.3 B.-1 C.-2 D.-3
(3)设A是一方阵,且AAT=E,则( ).
A.detA=1 B.detA=-1
C.detA=1或-1 D.detA=0
(4)设A、B均为方阵,且AB=O,则( ).
A.A=O且B=O B.A=O或B=O
C.detA=0且detB=0 D.detA=0或detB=0(www.xing528.com)
(5)设A、B、C均为n阶方阵,下面结论中,错误的是( ).
A.A+B=B+A B.(A+B)+C=A+(B+C)
C.AB=BA D.(AB)C=A(BC)
(6)设矩阵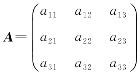
,Aij(i,j=1,2,3)是矩阵A的行列式detA中的元素aij(i,j=1,2,3)的代数余子式,则矩阵A的伴随矩阵是( ).
2.计算：
3.用矩阵变换求下列方程组的解：
4.k为何值时,方程组
只有零解?
5.判定矩阵
是否可逆,若是可逆的,求A-1.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
