9.4.1 矩阵的初等变换
先通过一个例子来理解矩阵的初等变换的含义.
引例 用消元法解如下线性方程组:


视频112
为了对比方程求解的过程中,方程组与方程组的系数以及常数项所构成的矩阵(这种矩阵我们称其为方程组的增广矩阵,而只有系数构成的矩阵又称为方程组的系数矩阵)的变化情况,我们把方程组在求解中的变化与对应的增广矩阵的变化分别列在表9-2的左、右两栏中.
表9-2

注:上表中所用的记号“ri↔rj”表示互换第i,j两行;“rj×k”表示行列式的第i行乘以数k;“ri+krj”表示将行列式的第j行乘以数k加到第i行.
从上面可以看出,用消元法求解线性方程组的过程就是对方程组进行下述三种变换:
(1)互换方程组中两个方程的位置;
(2)用一个非零常数乘某个方程;
(3)用一个非零常数乘某个方程后,加另一个方程.
显然线性方程组经过上述三种变换后所得到的方程组与原方程组是同解的.方程进行的这样的变换称为方程的初等变换.
从上例可见:当线性方程组在进行上述三种变换(即方程组进行初等变换)时,对应的增广矩阵也进行相应的变换,矩阵的这种变换被称为矩阵的初等变换.
定义9.9 对矩阵进行的
(1)互换矩阵的两行(常用“ri↔rj”表示将第i行与第j行互换);
(2)用一个非零常数乘矩阵中的某一行(常用“ri×k”表示将矩阵中第i行乘以数k);
(3)用一个非零常数乘某行后,加到另一行(常用“ri+krj”表示将矩阵的第j行乘以数k加到第i行).这种变换,称为矩阵的初等行变换.
与之类似,把上述定义中的“行”换为“列”,即得到矩阵的初等列变换的定义(其记号把r换成c).
矩阵的初等行变换与初等列变换,统称为矩阵的初等变换.
如果矩阵A经过有限次初等变换后,变成矩阵B,则称矩阵A与矩阵B等价,记作A→B.
显然,如果矩阵A与矩阵B等价,则矩阵B也与矩阵A等价.因为,如果矩阵A经过有限次初等变换后成为矩阵B,则用相反顺序,经过同样多次的适当的初等变换,就能够将矩阵B变成矩阵A.
9.4.2 利用初等变换求逆矩阵
若矩阵A的阶数较高时,用上节中定理9.4来求矩阵A的逆矩阵是非常困难的.还能找到其他的求逆矩阵的方法吗?
从上面的引例可以看出(表9-2的右边):一个可逆方阵A,经过一系列的初等变换总可以变换成同阶单位矩阵E.
可以证明,用同样的初等变换就把单位矩阵E变换成A-1,于是得到用初等变换求逆矩阵的方法:
![]()
例9.20 用初等变换求方阵

的逆矩阵.
解 因为


所以

一般来说,当矩阵的阶数较高时,用初等变换求逆矩阵比用伴随矩阵求逆矩阵(即用定理9.4)更简单.
注意:使用矩阵的初等变换求逆矩阵,对(A︙E)进行初等变换时,只能对(A︙E)用初等行变换,不能用初等列变换.
从前面的例题(包括用初等变换求逆矩阵的例题)中可以看到,在对矩阵进行初等变换时,常常是将一个矩阵A变换成为如下的两种形式之一的矩阵.
定义9.10 若矩阵B满足:
(1)零行(元素全为零的行)在下方;
(2)非零行的首非零元素(即该行中的第一个不为零的元素)的列标号随行标号的增加而严格递增.则称此矩阵B为行阶梯形矩阵(在不致混淆时,可以简称为阶梯形矩阵).
定义9.11 若阶梯形矩阵B满足:
(1)非零行的首非零元素都是1;
(2)所有首非零元素所在列的其他元素都是零.则称此阶梯矩阵为行简化阶梯形矩阵.
如
 (https://www.xing528.com)
(https://www.xing528.com)
均为阶梯形矩阵,其中,B2为行简化阶梯形矩阵.
例9.21 将矩阵

变换成为阶梯形矩阵,并求其行简化阶梯形矩阵.
解

上述过程所得的矩阵

就是A的行阶梯形矩阵.若将此矩阵继续进行初等变换,显然可以变换成为行简化阶梯形矩阵.
对上面的行阶梯形矩阵继续进行初等行变换:

上面最后所得的矩阵,就是矩阵A的行简化阶梯形矩阵.
由例题可见:
(1)任意一个矩阵A,通过初等行变换均可以变换为行阶梯形矩阵(这个行阶梯形矩阵称为矩阵A的行阶梯形矩阵),并可继续作初等行变换,将该行阶梯形矩阵变化成为行简化阶梯形矩阵(称这个行简化阶梯形矩阵为矩阵A的行简化阶梯形矩阵).
(2)一个矩阵的阶梯形矩阵不是唯一的,但一个矩阵的阶梯形矩阵中所含的非零行的行数是唯一的.矩阵的这一特征具有重要的作用.
9.4.3 矩阵的秩
1.矩阵秩的定义
定义9.12 从矩阵A中取k行k列,将位于这些行、列交叉处的元素,按原来的次序构成k阶行列式,该行列式称为矩阵A的k阶子式.
矩阵A的不等于零的子式的最高阶数就称为矩阵A的秩,记作R(A).
零矩阵的秩,规定为零.
例9.22 写出矩阵
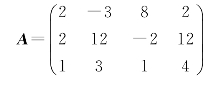
的全部三阶子式,并求该矩阵的秩R(A).
解 矩阵A共有四个三阶子式,具体如下:
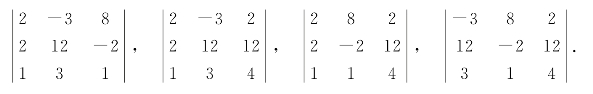
由计算可得,以上各行列式的值均为零,所以矩阵A的秩比3小.
因为可取到矩阵A的二阶子式

由定义得,矩阵A的秩R(A)=2.
由定义及上例知:
若矩阵A的秩R(A)=r,就相当于矩阵A至少有一个不为零的r阶子式,而所有比r阶高一阶(即r+1)的子式(如果有的话)全等于零.由行列式性质知,在行列式中当所有r+1阶子式全等于零时,所有高于r+1阶的子式也一定全等于零.因此,要确定矩阵A的秩为R(A)=r,我们只需要找到矩阵A的一个不为零的r阶子式(即Dr≠0),并验证矩阵A的所有r+1阶子式都等于零即可.
2.用初等变换求矩阵的秩
从上例可以知道,当矩阵的行、列数较大时,按上面的方法求矩阵的秩是很复杂的,是难以求出的.如何才能求出一个矩阵的秩呢?
根据矩阵的初等变换的特点,我们可以证明如下结论:
定理9.5 对矩阵A进行有限次初等变换成为矩阵B,有R(A)=R(B)(即初等变换不改变矩阵的秩).
定理9.6 行阶梯形(或行简化阶梯形)矩阵的秩等于其非零行的行数.
定理9.7 矩阵A与其转置矩阵AT的秩相等,即R(A)=R(AT).
因此,可用初等变换来求矩阵的秩,其步骤如下:先用矩阵的初等行变换将矩阵A变换成为行阶梯形(或行简化阶梯形)矩阵B;再由阶梯形(或行简化阶梯形)矩阵B中非零的行数得出矩阵A的秩.
例9.23 求矩阵

的秩及其转置矩阵AT的秩.
解 对矩阵A进行初等行变换
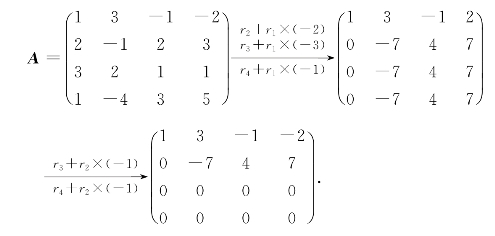
所以得
R(A)=2.
由行列式的性质及定理9.7,可得
R(AT)=R(A)=2.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




