解决方法如何求解方阵A的逆矩阵

在9.2节,若已知矩阵A和B且满足相乘条件时,用矩阵乘法,可以求出矩阵C,使AB=C；现在,若已知矩阵A和C,是否能求出矩阵B,使AB=C?

要解决此问题,要先讨论一个较简单的问题：对一个方阵A,能否求出一个同阶方阵B,使AB=E?

显然,并不是所有的方阵A都存在同阶方阵B,使AB=E.

视频111

9.3.1　逆矩阵的定义与性质

1.逆矩阵的概念

为解决上面提及的问题,先引入如下的定义：

定义9.7 设A为n阶方阵,若存在一个n阶方阵B,使

AB=BA=E,

则称方阵A是可逆的(简称A可逆),并称方阵B为A的逆矩阵(简称为A的逆阵或A的逆),记作A-1.即若AB=BA=E,则B=A-1.

例9.15 设有如下方阵A和B,验证方阵A是可逆的,且方阵B是A的逆矩阵.

解 因为

即有

AB=BA=E.

故由定义9.7得：方阵A是可逆的,而B是A的逆矩阵.

2.可逆矩阵的性质

定理9.2 设方阵A是可逆的,则A的逆矩阵是唯一的.

证明 设A有两个逆矩阵B和C,则

B=BE=B(AC)=(BA)C=EC=C,

所以,A的逆矩阵是唯一的.

定理9.3 如果方阵A可逆,则detA≠0.

证明 因为A可逆,即有A-1,使AA-1=E,于是就有

det(AA-1)=detE,

得

detA·detA-1=detE=1,

所以detA≠0.

3.方阵的逆矩阵满足的运算规律

(1)若方阵A可逆,则A-1也可逆,且(A-1)-1=A.

证明 因为A可逆,所以存在A-1,使

A-1A=AA-1=E,

所以A就是A-1的逆矩阵,即(A-1)-1=A.

(2)若方阵A可逆,数k≠0,则kA也可逆,且.

证明 因为

同时有

所以

(3)若A,B为同阶可逆方阵,则AB也可逆,且(AB)-1=B-1A-1.

证明 因为

(AB)(B-1A-1)=A(BB-1)A-1=AEA-1=AA-1=E,

同理有

(B-1A-1)(AB)=B-1(A-1A)B=B-1EB=B-1B=E,

所以

(AB)-1=B-1A-1.

(4)若方阵A可逆,则AT也可逆,且(AT)-1=(A-1)T.

证明 因为

(AT)(A-1)T=(A-1A)T=ET=E,

所以有

(AT)-1=(A-1)T.

9.3.2　伴随矩阵与逆矩阵的求法

通过前面的对逆矩阵概念与性质的讨论,对于矩阵A,只要A是一个可逆的方阵,则一定存在一个矩阵B=A-1,使AB=E.

由此可知,求上面问题中所述的矩阵B,就是求A-1,那怎么求出A-1呢?

首先,分析一个实例.(www.xing528.com)

由逆矩阵定义,得

B=A-1.

由于

若记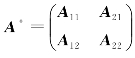(这里的矩阵A*称为矩阵A的伴随矩阵),则不难看出上例中的矩阵B具有如下特征结构：

即.

对于分析矩阵是否可逆以及求逆矩阵,上面的例题说明了什么?对于这个问题,由下面的定义与定理来回答.

定义9.8 由n阶方阵

的行列式detA中的元素aij的代数余子式Aij所构成的方阵

称为矩阵A的伴随矩阵,记为A*.

定理9.4 设A为方阵,若detA≠0,则A可逆,且*

证明 由行列式按行展开的性质及推论可知：

因detA≠0,所以有

同理有

所以就有

综合定理9.3和定理9.4可得：

①方阵A可逆的充分必要条件是detA≠0；

②这两个定理为分析矩阵是否可逆以及怎样求逆矩阵指明了方向.

例9.17 已知方阵

判定A是否为可逆矩阵,若是可逆矩阵,求其逆矩阵A-1.

解 因为

所以A可逆.

又因为

所以伴随矩阵

故A的逆矩阵为

由定理9.4及上例可知：求可逆矩阵A的逆矩阵A-1时,只要求出detA及伴随矩阵A*,再根据定理9.4即可.

9.3.3　用逆矩阵求解矩阵方程及求线性方程组的解

有了逆矩阵,对本节开始时所提出的“若已知矩阵A和C,是否能求得矩阵B,使AB=C?”的问题就可以回答了：只要A是可逆方阵且矩阵C的行数与方阵A的阶数相等,就一定存在一个矩阵B,使AB=C.

事实上,若A是可逆方阵,则A-1存在,就有A-1(AB)=A-1C,即有B=A-1C.

这是一个由已知矩阵A和C,求未知矩阵B的问题.对于这样的含有未知矩阵的等式,我们称其为矩阵方程.而求未知矩阵的过程,叫做求解矩阵方程.

显然,可用逆矩阵来求解矩阵方程,由下面例题可理解求解矩阵方程的方法.

例9.18 求解矩阵方程

解 记则方程可表示为AX=C.

由于

所以矩阵A可逆,且

于是

所以

还可以用逆矩阵的方法来讨论n元线性方程组的求解问题.

对于n元线性方程组式(9-5),如果记

则方程组式(9-5)就可写成矩阵方程

AX=B.

由此可见,只要矩阵A是可逆矩阵,则可用逆矩阵来解线性方程组

例9.19 用逆矩阵求解下列线性方程组：

解 设

方程组写成

AX=B.

由于detA==-1≠0,故A-1存在,由定理9.4,可求得

所以可得

所以,方程组的解为

注意：由例题可以看出,并不是所有的线性方程组都可以使用逆矩阵来求解,只有系数矩阵是可逆矩阵的线性方程组,才可使用逆矩阵来求解.

习题9-3答案