高等数学2版：矩阵的定义和运算

通过上一节的讨论知道,只有当线性方程组的个数与未知数的个数相等,且系数行列式不等于零时,才能用克拉默法则求出线性方程组的解.对于方程个数与未知数个数较多时,即使能用克拉默法则求出方程组的解,也是非常烦琐的.对于一般的线性方程组解的讨论,需要用矩阵这一重要的数学工具.

视频109

9.2.1　矩阵的定义

在科学技术、经济领域中,常常用到一些矩形数据表,例如某商场三个分场的两种商品一天的营业额(万元)见表9-1.

表9-1　单位：万元

常用矩形数据表简明表示

又如线性方程组式(9-5)中的各未知数的系数按在方程的位置次序不变可排成一个矩形数表

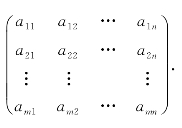
这样的矩形数表,在数学上就称为矩阵.

定义9.1 由m×n个数aij(i=1,2,…,m；j=1,2,…,n)排成m行n列的数表

被称为m行n列的矩阵,简称为m×n的矩阵.这里的m×n个数叫做矩阵的元素,aij叫做矩阵的第i行第j列的元素,i称为aij的行标,j称为aij,的列标.

矩阵通常可用大写字母A,B,C,…或用(aij),(bij),…等方法表示.有时,为了标明矩阵的行数m和列数n,常记作(A)m×n或(aij)m×n.

①当m=n时,称矩阵为n阶方阵.对于方阵,左上角至右下角的对角线为矩阵的主对角线；左下角至右上角的对角线为矩阵的次对角线.

②只有一行(即m=1)的矩阵(a11 a12 … a1n)叫做行矩阵.

③只有一列(即n=1)的矩阵

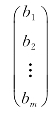
叫做列矩阵.

④元素都是零的矩阵叫做零矩阵,记作O.

⑤主对角线以外的元素都是零的方阵

叫做对角方阵.

⑥主对角线上的元素都是1,其他元素都是零的n阶方阵,叫做单位矩阵,记作En,在阶数不至于混淆时,可简记为E,即

⑦主对角线左下方的元素都是零的方阵

叫做上三角矩阵.

⑧主对角线右上方的元素都是零的方阵

叫做下三角矩阵.

⑨设A=(aij)m×n,B=(bij)m×n都是m行n列的矩阵.若它们对应的元素相等,即

aij=bij (i=1,2,…,m；j=1,2,…,n),

则称这两个矩阵相等,记作A=B.

⑩把m×n矩阵A的行列互换(即把所有的行换成相应的列)所得到的n×m矩阵,称为矩阵A的转置矩阵,记作AT,或者A′.

例9.8 设

已知A=B,求x,y,z.

解 因为A=B,根据矩阵相等,则可得

x=-2, y=1, z=-4.

注意：n阶方阵和n阶行列式是两个不同的概念,n阶行列式是一个数值,而n阶方阵不是一个数,而是n2个数排成的一个数表.

9.2.2　矩阵的运算

矩阵是线性代数的基本运算对象之一,下面讨论矩阵的基本运算.

1.矩阵的加法

引例 若某制造商在两个工厂F1,F2同时生产三种产品H1,H2,H3,上半年产量用矩阵表示(单位：件)为

下半年产量用矩阵表示为

则该制造商全年各工厂各产品的总产量可以用下面的矩阵表示：

也就是矩阵A与矩阵B的对应元素相加,就得到C,这样的运算就称为矩阵的加法.

定义9.2 两个m×n矩阵A=(aij)m×n,B=(bij)m×n的对应元素相加得到的m×n矩阵

称为矩阵A与B的和,记作C=A+B.

类似矩阵的和的定义,可以定义矩阵的减法,只需将加法中对应元素相加改为相减即可.

注意：由定义可知,两个矩阵只有在行数与列数对应相同时才能相加减.

2.矩阵的数乘

在前面引例中,若制造商各工厂生产各种产品的总量第二年、第三年分别与第一年完全一样,则三年各工厂生产各产品的总量可以用下述矩阵表示：

上面的矩阵D就是把矩阵C的每一个元素都乘以同一个数而得到一个矩阵,这样的运算就是数与矩阵的乘法.

定义9.3 设矩阵A=(aij)m×n,k∈R为常数,则矩阵B=(kaij)m×n称为数k与矩阵A的数乘,简称数乘矩阵,记作kA,即kA=(kaij)m×n.

例9.9 设

且3A-2X=B,求矩阵X.

解 由于A、B都是三阶方阵,所以,X也是三阶方阵,可设为

则

即

由相等矩阵的对应元素相等的性质,可得

视频110

3.矩阵与矩阵相乘

为理解矩阵的乘法,并能在实践中得到应用,先分析下列实例.

若用矩阵A表示某商场的三个分场两类商品的营业额,用矩阵B表示两种商品的国税率、地税率,即设(www.xing528.com)

则各分场应向国家财政和地方财政上交税额,可用如下矩阵表示：

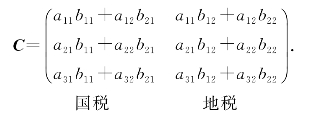
对于上面的矩阵C,可以看出,它的任意一元素cij是矩阵A的第i行的元素与矩阵B的第j列对应元素的乘积之和,即cij=ai1b1j+ai2b2j(i=1,2,j=1,2).这里的矩阵C就称为是矩阵A与矩阵B的乘积.

由此可得矩阵相乘的定义：

定义9.4 设矩阵A=(aij)m×l的列数与矩阵B=(bij)l×n的行数相同,则由元素

构成的m行n列矩阵

称为矩阵A与矩阵B的乘积,记为C=AB.

上述定义表明：

(1)乘积矩阵C的第i行第j列的元素cij,为左边矩阵A的第i行元素与右边矩阵B的第j列的对应元素乘积之和,如下所示：

(2)只有当左边的矩阵A的列数与右边的矩阵B的行数相等时,两矩阵才能相乘.

例9.10 设

求AB,BA,AC.

解

由上例不难看出,一般地：

①AB≠BA,即矩阵乘法不满足交换律；

②A≠O,B≠O,尽管有AB=O,也不能由AB=O得出A=O或B=O；

③AB=AC,A≠O但B≠C,说明矩阵乘法不满足消除律.

容易验证,矩阵乘法满足以下运算律.

①结合律：(AB)C=A(BC).

②分配律：(A+B)C=AC+BC,C(A+B)=CA+CB.

③k(AB)=(kA)B=A(kB),其中k为常数.

例9.11 已知

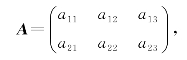
求AE3和E2A.

解

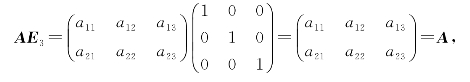
由此例看出：在矩阵乘法中,单位矩阵所起的作用与普通代数中数1的作用类似.一般有

Am×nEn=Am×n, EmAm×n=Am×n,可简记为：AE=EA=A.

由矩阵的乘积可以定义方阵的幂.

设A是n阶方阵,k为正整数,则

称为方阵A的k次幂.

由矩阵乘法的结合律,可得方阵的幂满足：

(1)AmAk=Am+k, (2)(Am)k=Amk (m、k为正整数).

但由于矩阵乘法不满足交换律,因此,一般情况下

4.矩阵的转置

定义9.5 矩阵的转置运算指的是求m×n的矩阵A的转置矩阵AT(或者A′)的运算

例9.12 求矩阵

的转置矩阵AT.

解 根据转置矩阵定义,可得

容易验证,矩阵的转置满足以下运算规律：

(1)(AT)T=A；　(2)(A+B)T=AT+BT；

(3)(kA)T=kAT；　(4)(AB)T=BTAT.

例9.13 已知

验证(AB)T=BTAT.

解 因为

所以

即

5.n阶方阵的行列式

定义9.6 把方阵A的元素按其原来的次序排列的行列式,称为方阵A的行列式,记作detA(或|A|).

例9.14 设

求A+B,3A,AB及detA,detB,det(A+B),det3A,detAB.

解 由矩阵的运算知

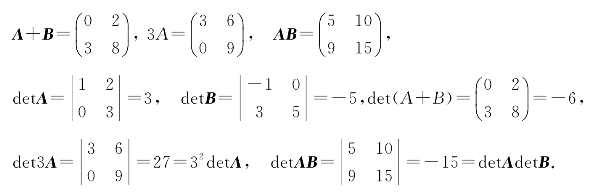
从上例可知：

(1)方阵与行列式是两个不同的概念.n阶方阵是n×n个数排成n行n列的一个数表,矩阵中的各元素没有任何运算关系,而行列式是一个数值.

(2)矩阵的加法与行列式不同.矩阵的加法是对应元素相加,行列式则是两个数相加.一般地,det(A+B)≠detA+detB.

(3)“数与矩阵相乘”和“数与行列式相乘”也是不同的概念.数与矩阵的乘法是用数乘矩阵的每一个元素,而数与行列式相乘只是用数乘行列式的某一行(或列)的各元素.

(4)方阵的行列式满足以下运算规律.

①det(AT)=detA；

②det(kA)=kndetA；

③det(AB)=det(BA)=detAdetB.