高等数学下册：微分方程应用举例

前面讨论了几种微分方程的求解方法,本节将通过举例介绍微分方程的一些简单的应用和利用微分方程解决实际问题的一般步骤.

8.7.1　一阶微分方程的应用举例

例8.25 一曲线通过点(2,3),在该曲线上任意一点P(x,y)处的法线与x轴交点为Q,且线段PQ恰被y轴平分,求曲线的方程.

解 如图8-2所示,设所求曲线的方程为y=f(x),则它在点

P(x,y)处的法线方程为

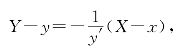
令Y=0,得法线与x轴交点Q的横坐标为

X=yy′+x.

由题中的线段PQ恰被y平分的条件,得

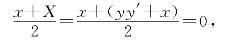
因此可得曲线y=f(x)满足微分方程

yy′+2x=0.

又由于曲线过点(2,3),得初值条件

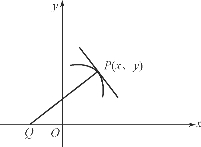
图8-2

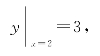
将方程yy′+2x=0分离变量,得

ydy=-2xdx,

两边积分,可得

将初值条件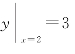代入上式,确定c=17,则所求曲线的方程就为

y2+2x2=17.

例8.26 加热后的物体在空气中冷却的速率与每一瞬时的物体温度与空气温度之差成正比,试确定物体温度T与时间t的函数关系.

解 设物体温度T与时间t的函数关系为T=T(t),空气的温度为T0,则物体冷却的速

率就是温度T对时间t的变化率. 由题意知,T=T(t)满足方程

其中,k＞0为比例常数(由于当T＞T0时,物体温度下降,即有故上式右边取负号),分离变量得

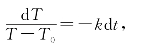
积分可得

例8.27 如图8-3所示的电路中,电动势E、自感L与电阻R及都是常数,若开始时(t=0)回路电流为i0,求任一时刻t的电流i(t).

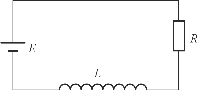
图8-3

解 设回路中,t时刻的电流为i(t),由电学定律可知,回路中的电源电动势,等于回路中各元件产生的电压降,所以有

即

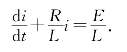
由于开始时(t=0)回路电流为i0,故初值条件为

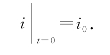
由于方程是一阶非齐次线性微分方程,由一阶非齐次线性微分方程通解公式,得

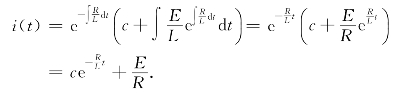
将初值条件代入通解,得,则所求电流为

8.7.2　二阶微分方程的应用举例

例8.28 火车沿水平直线轨道运动,设火车质量为M,机车牵引力为F,阻力为a0+b0v,其中a0,b0为常数,v为火车的速度.若已知火车的初速度与初始位移都是零,试求火车的运动方程.

解 设火车的运动方程为s=s(t),由导数的物理意义知

由题意有

由牛顿第二定理知

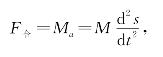(https://www.xing528.com)

所以,得微分方程

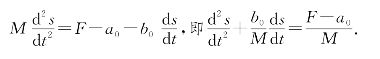
由题意知,初值条件为

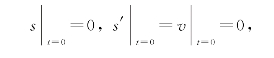
由特征方程

得特征根为

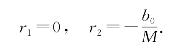
因微分方程的右边为,是个常数,故可设方程的特解s*=At.

将s*=At代入方程得

所以,方程的通解为

由初值条件得

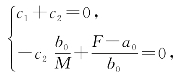
所以

故火车的运动方程为

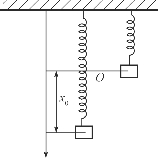
图8-4

例8.29 设有一弹簧,它的上端固定,下端挂一个质量为m的物体,平衡位置为O点(图8-4),若将物体向下拉一段距离x0后放开,让它自由上下振动,试求物体运动的微分方程(假设物体运动时没有阻力).

解 设在t时刻,物体离开平衡位置x(t),由胡克定律知,物体受

弹簧作用的力为

F=-cx(t),

其中c为弹性系数,负号表示物体力的方向与位移相反.

由牛顿第二定律F=ma,可得

即物体运动的微分方程为

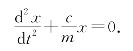
初值条件为

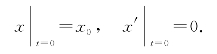
例8.30 试求由微分方程y″-y=0所确定的一条积分曲线y=y(x),使它在点(0,1)处与直线y+3x=1相切.

解 由题意知,所求积分曲线y=y(x)满足二阶常系数齐次微分方程y″-y=0,初值条件为y(0)=1,y′(0)=-3.

由特征方程r2-1=0,得特征根为

r1=-1, r2=1,

故方程y″-y=0的通解为

y=c1e-x-c2ex.

将初值条件y(0)=1,y′(0)=-3代入通解,得

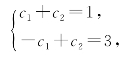
解得c1=-1,c2=2,故所求积分曲线的方程为

y=-e-x+2ex.

通过上述例题的讨论可以看到,我们在建立微分方程并用其解决实际问题时,可按如下步骤进行：

(1)根据题设条件,利用已知的公式、定理或定律,建立相应的微分方程,确定初值条件；

(2)分辨所建立的微分方程的类型,运用相应解法求出其通解；

(3)利用初值条件,确定通解中的任意常数,求得满足初值条件的特解；

(4)根据实际问题的需要,利用所求得的特解来解释问题的实际意义或求得题设所需的其他结果.

在以上的四个步骤中重点是列出方程和求解方程,解决实际问题的关键是建立微分方程.

习题8-7答案