微分方程基本概念，高等数学下册

首先分析几个实例,然后再介绍微分方程的基本定义.

视频99

例8.1 一曲线过点(1,-1),且该曲线上任意一点处的切线斜率等于横坐标平方的倒数,求这条曲线的方程.

解 为了求这曲线的方程,可设所求的曲线的方程为y=f(x).

由导数的几何意义可知,未知函数y=f(x)满足如下关系式：

由题设条件还知道,未知函数y=f(x)还满足

对式(8-1)两边积分,得

将条件(8-2)代入式(8-3),得

c=0.

将c=0代入式(8-3)中,得所求曲线的方程为

例8.2 将质量为m的物体在离地面高度h处以初速度v0向上抛出,试求物体的运动规律(不考虑空气阻力).

解 过上抛点作一铅直向上直线,以该直线与地面的交点为原点,铅直向上为正轴方向建立坐标系(图8-1),并从物体上抛的时刻开始计时.

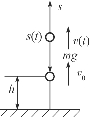
图8-1

设在t时该物体的位置为s=s(t),由一阶导数和二阶导数的物理意义知,物体在t时刻的速度和加速度各为

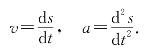
由于不考虑空气阻力,则

据题意,s=s(t)满足

对式(8-5)积分一次,得

再对式(8-7)积分一次,得

以上式中的c1,c2是任意常数.

将条件代入式(8-7),得

c1=v0,

将条件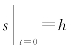及c1=v0都代入式(8-8),得

c2=h.

将所求的c1=v0及c2=h代入式(8-8),即得物体运动的方程

在上面两例中,关系式(8-1)和关系式(8-5)都含有未知函数的导数(或微分),尽管两例的实际意义不相同,但解决问题的方法是相同的,即在建立起一个含有未知函数的导数(或微分)的关系式后,通过此关系式求出满足所给附加条件的未知函数.

一般而言,这种含有未知函数的导数(或微分)的方程,称为微分方程；而由微分方程求出未知函数的过程,称为求解微分方程.在微分方程中,若未知函数是一元函数,则称这种微分方程为常微分方程；若未知函数是多元函数,则称这种微分方程为偏微分方程.例如,在上面两例中的式(8-1)和式(8-5)均是常微分方程.本章我们只讨论常微分方程,为方便,简称为微分方程(或方程).

在微分方程中出现的未知函数的导数的最高阶数称为微分方程的阶；若微分方程的阶为n,则称此方程为n阶微分方程.

例如,方程式(8-1)是一阶微分方程,方程式(8-5)是二阶微分方程.

如果把某个已知函数及其导数代入微分方程中,使方程的左、右两边恒等,则称此函数为微分方程的解.如例8.1中的函数式(8-3)与函数式(8-4)都是微分方程式(8-1)的解,例8.2中的函数式(8-8)与函数式(8-9)都是微分方程式(8-5)的解.

从上面两例还可以看出,例8.1中的函数式(8-3)和函数式(8-4),例8.2中的函数式(8-8)与函数式(8-9)虽然各都是方程式(8-1)、方程式(8-5)的解,但所表示的解的含义是不相同的,解的形式也是不相同的.(www.xing528.com)

如果微分方程的解中含有相互独立的任意常数,且个数与微分方程的阶数相同,则这样的解称为微分方程的通解；而不含任意常数的微分方程的解,称为微分方程的特解.如例8.1中的式(8-3),例8.2中的式(8-8)分别是微分方程式(8-1)、式(8-5)的通解；而例8.1中的式(8-4)、例8.2中的式(8-9)分别是微分方程式(8-1)、式(8-5)的特解.

在例8.1中,微分方程式(8-1)的解式(8-4)是由附加条件式(8-2)将通解式(8-3)中的任意常数c确定所得的；在例8.2中,微分方程式(8-5)的解式(8-9)是由附加条件式(8-6)将通解式(8-8)中的任意常数c1,c2确定所得的,这种用于确定微分方程通解中的任意常数的值的条件,称为微分方程的初值条件(也叫做定解条件).

例如,例8.1中的式(8-2)、例8.2中的式(8-6)各是方程式(8-1)与式(8-5)的初值条件.

由初值条件确定了通解中的任意常数的值之后所得到的微分方程的解称为微分方程满足初值条件的特解.

例如,例8.1中的式(8-4)是微分方程式(8-1)满足初值条件式(8-2)的特解；例8.2中的式(8-9)是方程式(8-5)满足初值条件式(8-6)的特解.

求满足初值条件的特解的问题,称为初值问题.

一般而言,一阶微分方程的初值条件写成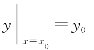或写成y(x0)=y0；二阶微分方程的初值条件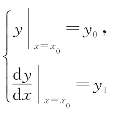写成或写成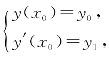其中的x0,y0,y1为已知数.

例8.3 验证函数y=c1e2x+c2e-2x(c1,c2为任意常数)是方程y″-4y=0的通解,并求满足初值条件的特解.

解 因为y′=2c1e2x-2c2e-2x,y″=4c1e2x+4c2e-2x,

将y、y″代入微分方程中,得

所以,函数y=c1e2x+c2e-2x是微分方程y″-4=0的解.

由y=c1e2x+c2e-2x的形式可知,c1,c2不能合并为用一个任意常数表示,所以它们是两个相互独立的任意常数,而微分方程y″-4y=0的阶数是2,说明该解中所含的相互独立的任意常数个数与微分方程的阶数是相等的,所以,y=c1e2x+c2e-2x是微分方程y″-4y=0的通解.

将初值条件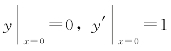分别代入

y=c1e2x+c2e-2x和y′=2c1e2x-2c2e-2x,

得

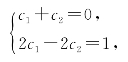
解得.

所以,所求的特解为.

例8.4 求微分方程y‴=x+1的通解.

解 将方程y‴=x+1求积分,得

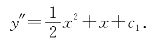
对上式两边求积分,得

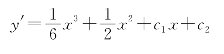
再对上式两边积分,得

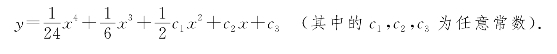
例8.5 下列函数中,哪些是方程y′-2y=0的解?哪一个是满足初值条件的特解?

(1)y=sin2x；　(2)y=e2x；　(3)y=3e2x.

解 (1)因为y′=2cos2x,将y=sin2x及y′=2cos2x代入方程y′-2y=0,得：左边=2cos2x-2sin2x≠0,即左边≠右边.

所以,函数y=sin2x不是方程y′-2y=0的解.

(2)因为y′=2e2x,将y=e2x及y′=2e2x代入方程y′-2y=0,得：

左边=2e2x-2e2x=0,即 左边=右边.

又将x=0代入y=e2x,求得y=1,即满足,

所以,函数y=e2x是方程y′-2y=0的解,且是满足初值条件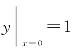的特解.

(3)因y′=6e2x,将y=3e2x及y′=6e2x代入方程y′-2y=0,得：

左边=6e2x-6e2x=0,即左边=右边.

而将x=0代入y=3e2x,求得y=3≠1,

所以,函数y=3e2x是方程y′-2y=0的解,但不是满足初值条件的特解.

习题8-1答案