高等数学·下册（第2版）中的幂级数与收敛域

前面研究的级数是常数项级数,即级数的各项都是常数.本节研究函数项级数,重点讨论幂级数.

7.4.1　函数项级数与幂级数的定义

如果级数的每一项un都是函数un(x)(x∈I),则称该级数为函数项级数,一般可表示为

对函数项级数,给x以一个确定的值,如x=x0∈I时,则函数项级数(7-1)就成为一个常数项级数

如果常数项级数(7-2)收敛,则称x0为函数项级数(7-1)的收敛点；如果常数项级数(7-2)发散,则称x0为函数项级数(7-1)的发散点.

对于函数项级数,收敛点、发散点往往都不止一个,我们把函数项级数(7-1)的收敛点的全体称为它的收敛域,而函数项级数(7-1)的发散点的全体,就称为它的发散域.

如果函数项级数(7-1)在其收敛域内取任意一点x,函数项级数(7-1)成为一个常数项级数,因而必有一个确定的和.因此,在收敛城上,函数项级数(7-1)的和就是x的函数,记作s(x),我们称s(x)为函数项级数(7-1)的和函数.显然,和函数的定义域就是函数项级数(7-1)的收敛域,在收敛域上,有

若用sn(x)表示函数项级数(7-1)的前n项的和

sn(x)=u1(x)+u2(x)+…+un(x),

则在函数项级数(7-1)的收敛域上,有

由此可见,讨论函数项级数,重要的是分析其收敛域及求其和函数.但函数项级数比常数项级数要复杂得多,为此,仅讨论其中结构简单、应用广泛的一种函数项级数,即幂级数.

视频92

定义7.4 形如

的函数项级数称为幂级数,其中,x0及a0,a1,a2,…,an,…都是常数,常数a0,a1,a2,…,an,…称为幂级数的系数.

当x0=0时,幂级数(7-3)成为

如

都是幂级数.

幂级数(7-4)是一种特殊形式的幂级数,也是最为重要的一种幂级数(为了后面学习的需要,我们把这种形式的幂级数称为标准形式).由于形如式(7-3)的幂级数(这种形式的幂级数我们把它称作为一般形式),可以通过令x-x0=t的变量代换将其转化为形如式(7-4)形式的幂级数,因此,本书主要讨论形如式(7-4)的幂级数的收敛域,研究它在收敛域上的性质.

7.4.2　幂级数的收敛半径及收敛区间

我们首先来解决求幂级数收敛域的问题.

从幂级数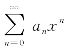的形式可以看出,当取x=0时,显然,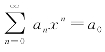(因为当取n≥1时,级数各项的值都是0),即级数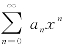在x=0处一定是收敛的；而在x≠0,级数可能是收敛,也可能是发散的.

如果幂级数不是仅在x=0处收敛,那么,幂级数不是在整个实数范围收敛,就一定在实数范围内存在一个使幂级数收敛的集合.

可以证明：若幂级数不是仅在x=0处收敛或者整个实数范围内收敛,则一定存在一个正实数R＞0,使幂级数：

(1)当|x|＜R即x∈(-R,R)时,幂级数收敛；

(2)当|x|＞R即x∞(-∞,-R)∪(R,+∞)时,幂级数发散；

(3)当|x|=R即x=±R时,幂级数可能收敛,也可能发散.

这里的正实数R,称为幂级数的收敛半径,并称区间(-R,R)为幂级数的收敛区间.

可见,要求幂级数的收敛域,关键是求它的收敛半径,那么如何求收敛半径呢?根据正项级数比值审敛法,可以得到下述定理：

视频93

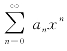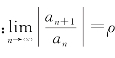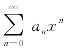定理7.7 若幂级数的系数满足,则幂级数的收敛半径为

可见,由定理7.7容易求出幂级数的收敛半经,进而可解决求幂级数的收敛域的问题.

例7.14 求下列幂级数的收敛半径和收敛域：

解 (1)因为

所以,收敛半径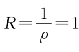,级数的收敛区间为(-1,1)；

因为当取x=1时,级数成为

是收敛的交错级数.

当取x=-1时,级数成为

是发散的,因此,级数的收敛域为(-1,1].

(2)因为

所以,级数的收敛半径=4,收敛区间为(-4,4).

因为,当取x=4时,级数成为

而,由级数收敛的必要条件知,级数发散.

当取x=-4时,级数成为

也是发散的,故级数的收敛域为(-4,4).

(3)因为

所以级数的收敛半径R=0,该级数仅在点x=0处收敛,收敛域为{x|x=0}.

(4)因为

所以,收敛半径R=+∞,级数收敛域为(-∞,+∞).(www.xing528.com)

从例7.14可以看到,对于符合定理7.7要求的幂级数,要求此幂级数的收敛半径以及收敛域都可以先应用定理7.7求出收敛半径,尔后分析收敛域.如果题目中的幂级数的形式与定理7.7不相符合,如何求幂级数的收敛半径和收敛域?下面的例题给出了几种形式的求解方法.

例7.15 求下列级数的收敛半径和收敛域：

解 (1)因为级数缺x的奇次项,所以不能直接用定理7.7求收敛半径,但可通过变量代换将其化为形如式(7-4)的级数.

视频94

令x2=t,原级数化为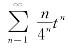,对此级数,由于

所以=4,当|t|＜4即x2＜4时,级数收敛.

因此,当|x|＜2时,原级数收敛,故收敛半径为R=2.

因为当取x=±2时,幂级数成为,是发散的,

所以,级数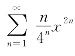的收敛域为(-2,2).

(2)因为级数缺x的偶次项,所以不能直接用定理7.7求收敛半径,但根据正项级数比值审敛法,有

(3)此级数是形如式(7-3)的幂级数,可通过下列的变量代换化为形如式(7-4)的级数.

令t=x+1,则所给级数变形为而对此级数,有

由此可知收敛半径R=1,当|t|＜1时,级数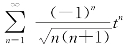收敛,就知当|x+1|＜1即-2＜x＜0时,也收敛.故级数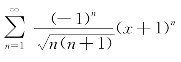的收敛区间为(-2,0).

当x=-2时,级数变为

是发散的；

当x=0时,级数为

是收敛的交错级数.所以,级数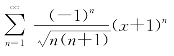的收敛域为(-2,0].

视频95

7.4.3　幂级数的运算性质

在利用幂级数解决实际问题时,经常要对幂级数进行加、减以及求导、求积分等运算,幂级数在进行这些运算时,有如下性质.

性质1 设幂级数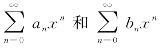的收敛半径各为R1,R2,和函数分别为s1(x),s2(x),则幂级数

的收敛半径R=min{R1,R2},且和函数s(x)=s1(x)±s2(x).

通过这个例子我们可以注意到,在讨论一个比较复杂的幂级数的收敛半径与和函数时,可以利用性质1把其拆分成若干个较简单的幂级数,然后从讨论这些简单幂级数的收敛半径与和函数入手,最终得到较复杂的幂级数的收敛半径与和函数.

性质2 设幂级数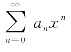的收敛域为区间I,则其和函数s(x)在区间I内是连续的.

性质3 (逐项求导的性质)设幂级数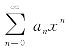的收敛半径为R＞0,其和函数为s(x),则在区间(-R,R)内,和函数s(x)可导,且有

性质4 (逐项积分的性质)设幂级数的收敛半径为R＞0,其和函数为s(x),则在区间(-R,R)内,和函数s(x)可积,且有

性质3和性质4分别表明,幂级数在其收敛域内可以进行逐项求导运算和逐项积分的运算.

比如：我们都知道

因此,我们根据性质3,可以在区间(-1,1)内,由上式的两边对x逐项求导数,得到

这样就得到了一个新的幂级数的和函数,而这个和函数可以帮助我们求解收敛级数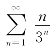[例7.11(1)]的和数,即

但如果我们是在区间(-1,1)内,根据性质4两边逐项积分的话,那得到的就是另一个幂级数的和函数：

而这个幂级数的和函数又可以帮助我们去求解收敛级数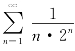的 和数(例7.6),即

所以,通过以上的讨论我们看到,前面我们在学习常数项级数敛散性的判断时,一直在回避求解收敛级数的和数问题,现在有了幂级数的和函数概念后,我们发现可以借用和函数来求解部分收敛级数的和数了.

幂级数的代数运算、逐项求导运算及逐项积分运算的性质有着重要的意义,也是间接求解幂级数和函数及收敛半径、收敛域的一种重要的方法.

例7.17 利用幂级数性质,求下列幂级数的和函数及收敛域：

解 (1)设级数的和函数为s(x),即

由幂级数的性质4(逐项积分的性质),得

对上式两端关于x求导,得

所以得

而当x=±1时,级数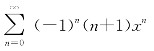显然发散,所以得级数的收敛域为(-1,1).

(2)设级数的和函数为s(x),即

由幂级数逐项求导的性质,得

两边积分,得

即

所以

而当x=±1时,幂级数成为或,都是发散的,所以,幂级数的收敛域为(-1,1).

习题7-4答案