高等数学：绝对收敛与条件收敛

7.2节介绍了正项级数及判别其敛散性的方法,本节先研究交错级数的敛散性判定方法,然后再讨论任意项级数敛散性的判定方法.

视频90

7.3.1　交错级数及审敛法

一个级数的各项如果是正负相间的,则称该级数是交错级数,一般地,交错级数可以表示为

其中,un(n=1,2,3,…)都是正数.

交错级数有如下重要的审敛法.

定理7.4 (莱布尼茨准则)若交错级数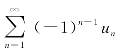满足条件

则级数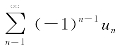收敛.

例7.12 判别下列级数的敛散性：

且

所以,级数收敛.

视频91

7.3.2　绝对收敛与条件收敛(www.xing528.com)

如果常数项级数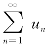中的一般项un为任意实数,则称这样的级数为任意项级数.现在来研究判定任意项级数敛散性的问题.

讨论一个任意项级数的敛散性,往往借助正项级数的审敛法来讨论.

设级数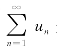是一个任意项级数,如果将其各项均取绝对值,就得到一个正项级数.

需要注意：

结合正项级数的比值审敛法,可以得到如下定理：

(3)当λ=1时,则此法无效.

例7.13 判定下列级数的敛散性,若收敛,指明是绝对收敛还是条件收敛.

(2)因为

从上面的例题可以看出：分析任意项级数的敛散性时,一般可按如下步骤进行：

(1)先用定理7.6进行分析,若分析结果符合定理7.6,则讨论结束；

(2)若不符合定理7.6的条件(即λ=1或不存在)时,则再考虑使用其他方法(如正项级数的比较审敛法、交错级数的莱布尼茨准则、收敛与发散的定义以及级数的性质等)来判定.

习题7-3答案