高等数学下册：正项级数及审敛法

对于一个级数来说,要考虑的问题主要有以下两个方面：

(1)级数是否收敛?即当给出一个级数时,我们如何来判定该级数是否收敛?

(2)当级数收敛时,求出它的和；这个和是如何求出的呢?

在一般情况下,可以利用级数收敛与发散的定义、性质来判断一个级数的敛散性,但常常是很困难的,因此需要建立判断级数敛散性的审敛法.本节主要介绍正项级数及其审敛法.

如果级数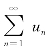的每一项都是非负数,即un≥0(n=1,2,3,…),则称该级数为正项级数.

正项级数是一类重要的级数,在研究其他级数的敛散性问题时,往往归结为研究正项级数的收敛性.

由于正项级数的通项有un≥0,所以其部分和数列s1,s2,…,sn,…是单调增加的,即s1≤s2≤…≤sn≤…

由数列极限的存在准则(即单调有界数列必有极限)知,只要级数的部分和数列{sn}有上界,正项级数必收敛.由此推出以下三种判定正项级数敛散性的审敛法.

7.2.1　比较审敛法

比较审敛法(即定理7.1)告诉了我们一个很朴实的道理,在两个大小不一和式的比较过程中,如果更大的那个和式是已知可以加起来的(即收敛),那么较小的那个和式自然也是可以加起来的(即也是收敛的)；反之较小的和式如果已知是加不起来的(即发散),那更大的那个和式肯定也是无法相加的(即也是发散的).

解 由于当x＞0时,有不等式x＞ln(1+x)成立,所以

视频87

当p＞1时,因为

从上面的例子可以看出,运用比较审敛法的关键是找到一个已知敛散性的正项级数,通过比较二者通项的值的大小,来确定未知级数的敛散性.

注意：在用比较审敛法判断级数敛散性时,我们常用来进行比较的级数有：

其中当p=1时为调和级数,所以调和级数只是p-级数的一种特例.熟记以上级数的敛散性,将有利于比较审敛法的运用.

例7.9 判定下列级数的敛散性：

解 (1)因为n(n+1)＜(n+1)2,故有

所以

又,级数

(2)因为

所以

运用比较审敛法时,要先找一个已知敛散性的级数,再比较通项值的关系,这对初学者来说,往往难以把握.(www.xing528.com)

7.2.2　极限审敛法

视频88

注意：

(1)因为必要条件是有它不咋的,而没它是不行的,所以必要条件说明不了什么,但我们往往可以用必要条件来否定问题：

(2)要想利用好定理7.2,必须具备一定的极限计算技能,尤其是掌握当x→∞时,多项式之比的极限计算公式,即

例7.10 判定下列级数的敛散性：

7.2.3　比值审敛法

用比较审敛法判定级数的敛散性时,如果将待审级数与几何级数作比较,并表达成极限形式的话,便可得到下面的比值审敛法.相比前两种审敛法来讲,比值审敛法更直截了当,应用起来也十分方便,并且我们在后期的学习讨论中,会反复用到这种方法.

视频89

注意：当λ=1时,此审敛法无效,级数的敛散性不能确定(即可能是收敛的,也可能是发散的),其敛散性需用其他方法来判定.

例7.11 判定下列级数的敛散性：

解 (1)因为

所以,由比值审敛法知,级数收敛.

(2)因为

所以,由比值审敛法知,级数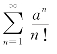(a＞0)收敛.

(3)因为

若,得

(4)因为

故由比值审敛法知,级数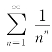收敛.

从例题可以看出：在判定正项级数敛散性时,感觉到比值审敛法比比较审敛法更好、更容易掌握,因此觉得只要掌握比值审敛法就行了.这种想法是不对的,因为没有哪一种方法能解决所有的问题.其实每种审敛法各具特点,不存在哪种审敛法更重要的问题,它们之间是相辅相成的.

习题7-2答案