无穷级数的基本概念和性质–《高等数学·下册》

7.1.1　无穷级数的基本概念

引例 在我国东汉时期的数学巨著《九章算术》一书中,记载有“一尺之棰,日取其半,万世不竭”这样一段话,这段话用数学式子说明,其含义是：

常数1可以表示为：反过来,这无穷多项累加的结果是1,即

在实践中,类似这种无穷多项累加的问题有许许多多.为此,对这种无穷多个数求和的问题,我们给出下面的定义：

视频83

定义7.1 设给定一个数列

u1,u2,u3,…,un,…

则表达式

u1+u2+u3+…+un+…

称为无穷级数,简称级数,记作,即

其中,un称为级数的第n项,也称为一般项或通项.

级数的前n项之和：u1+u2+…+un记为Sn,称为级数的前n项部分和,简称为级数的部分和.

在级数中,若通项un是常数,则级数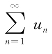称为常数项级数(简称为数项级数).

级数(1)、(2)都是常数项级数,级数(3)、(4)都是函数项级数.

由定义7.1可知,无穷级数是无穷多个数累加的结果,因此不能按求有限个数的和那样直接把它们逐项相加.但前面的引例已为我们提示了方法：即先求有限项的和,然后运用极限的方法来解决这样的无穷多项的累加问题.

例7.1 求级数：1++…的和.

解 设sn表示级数前n项的和,s表示该级数的和,则有

可看出,当n不断增大时,sn与s越接近,由极限知识可知n→∞时,sn→s,即.

因此,我们只要求出sn,再求出即可求出级数的和.

由级数的形式知道,这是一个公比的无穷等比数列组成的级数,其前n项和

显然

由极限知识可知,当n→∞时,sn→2,其意义就是：随着所加的项数n的不断增加并趋向无穷大,级数的部分和sn越来越接近级数的和,所以

由此可见,我们在讨论无穷多个数的和数(即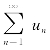的结果)是否存在时,与级数的前n项的和sn=u1+u2+…+un的极限有关.为此我们给出如下定义：

定义7.2 对于无穷级数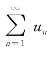的前n项的和sn,如果当n→∞时,sn的极限存在为s,即

则称级数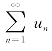是收敛的,并称s为该级数的和数.可记为

如果n→∞时,sn没有极限,即不存在,则称该级数是发散的.当级数发散时,和数自然是不存在.

视频84

当级数收敛时,其和s与它的部分和sn之差

rn=s-sn=un+1+un+2+…

称为级数的余项.显然,级数收敛的充分必要条件是.

很显然,我们学习无穷级数事实上就是在讨论无穷个数的和的运算问题(注：这里也不排除减法运算,减法可以看成是一个正数与一个负数的和).其结果不外乎两种：一种是无穷个数能加起来(即它们的和数存在),这种情况我们称级数是收敛的；而另一种情况则是无穷个数无法加起来(即它们的和数不存在),这种情况我们称级数是发散的.由于是无穷项相加(减),因此我们在这里不可能用常规的加减手段(就是有限个数的加、减运算)去处理,所以才有了上面的定义7.2.下面我们就用定义7.2来判断级数的敛散性,同时在级数收敛的情况下求出其和数.

例7.2 判断下列级数的敛散性,若收敛,求其和：

解 (1)因为级数的部分和

而,所以级数发散.

(2)因为级数的部分和

从而有=1,

所以级数是收敛的,且级数的和s=1.

(3)因为级数的部分和

而　所以级数是发散的.

(4)因为

而所以=∞.

因此级数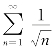是发散的.(www.xing528.com)

由上面的例题可以看出：使用定义7.2来讨论级数的敛散性时,首先必须求出此级数的前n项和sn,然后分析极限是否存在.若极限存在,则该级数是收敛的,否则,级数是发散的.如果说级数的前n项和Sn求不出来的话,就要用其他的方法来讨论.

例7.3 分析几何级数(等比级数)

的敛散性.

解 由等比数列求和公式,当公比|q|≠1时,级数的部分和

当|q|＜1时,从而

所以级数收敛.

当|q|＞1时,从而

所以级数发散.

而 当q=1时,显然sn=na,从而有

所以级数发散.

当q=-1时,级数成为a-a+a-a+…,若n是奇数时,有sn=a,而若n是偶数时,有sn=0.因而,当n→∞时,sn的极限不存在,级数发散.

综上所述：

当|q|＜1时,几何级数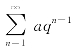是收敛的,它的和,

即；

当|q|≥1时,几何级数aqn-1是发散的.

视频85

7.1.2　无穷级数的基本性质

判定级数的敛散性,虽然可以使用级数收敛、发散的定义来进行,但对于形式复杂的级数,使用这种方法往往是很困难的,甚至无法判定.判定级数的敛散性,常常要使用级数的性质.无穷级数主要有如下性质：

性质1 若级数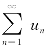收敛,其和为s,则对任一常数c,级数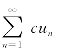也收敛,且和为cs.若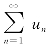是发散的,则对任一不为零的常数c,级数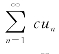也发散(证明从略).

性质2 若级数都收敛,和分别为s1、s2,则级数也收敛,且和为s1±s2(证明从略).

例7.4 判别级数的敛散性,若收敛,求其和.

解 级数可表示为

因为级数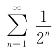是公比的等比级数,它是收敛的,且其和为

而级数是公比的等比级数,它是收敛的,且其和为

由性质2可知,

级数即级数是收敛的,且其和为

性质3 一个级数增加或减少有限项,不改变级数的敛散性(证明从略).

注意：一个级数增加或减少有限项后,虽然其敛散性不变,但一般情况下,收敛级数的和会发生改变.

如等比级数是收敛的,减去它的前五项,得到级数为

该级数显然收敛,但前一级数的和为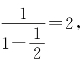后一级数的和为.

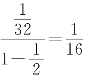性质4 若级数收敛,将级数中的项任意合并(即加上括号)后所成的级数仍收敛且其和不变(证明从略).

注意：一个级数若合并项后所成的级数收敛,并不能保证原有级数是收敛的.

例如,级数1-1+1-1+…+1-1+…

是发散的,但按如下方式合并项：

(1-1)+(1-1)+…+(1-1)+…

该级数显然收敛,且和为零.

由性质4可知,若合并项后所成的级数发散,则原有级数必发散；若原有级数收敛,则合并项后所成的级数也收敛.

例7.5 证明级数

是发散的.

证明 由于级数的通项为

习题7-1答案