高等数学·下册：二重积分的定义、性质与计算

在上册第5章,我们讨论了定积分.定积分的被积函数是一元函数,积分区域是数轴上的一个区间.而将被积函数由一元函数y=f(x)推广到二元函数z=f(x,y),积分范围由x轴上的闭区间[a,b]推广到xOy平面上的闭区域D,就是二重积分.本节通过引例介绍二重积分概念,然后学习二重积分的性质与计算.

视频81

6.6.1　二重积分的定义

1.引例——曲顶柱体的体积

若有一个柱体,它的底是xOy平面上的闭区域D,它的侧面是以D的边界曲线为准线,且母线平行于z轴的柱面,它的顶是曲面z=f(x,y).设f(x,y)≥0为D上的连续函数,则称这个柱体为曲顶柱体(图6-20).下面求其体积V.

(1)分割：将区域D任意分割成n个小块Δσ1,Δσ2,…,Δσn,且Δσi也表示第i个小块的面积,这样就将曲顶柱体相应地分割成n个小曲顶柱体,它们的体积记为ΔVi(i=1,2,…,n).

(2)求和：记di为Δσi的直径.则当di很小时,在Δσi中任取一点(ξi,ηi),以f(ξi,ηi)为高且以Δσi为底的平顶柱体的体积为f(ξi,ηi)Δσi,可以将其看作是以Δσi为底的小曲顶柱体体积的近似值.因此,曲顶柱体的体积可以取近似值为

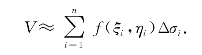
(3)取极限：若记λ=max{d1,d2,…,dn},则

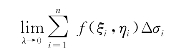
为所求曲顶柱体的体积V.

由此可看出：曲顶柱面的体积最后都归结为求引例中的这一和式的极限.在很多的实际问题的解决中,也与此类似,可以表示成这样的极限形式.为此,就得到了二重积分的定义.

2.二重积分的定义

定义6.5 设z=f(x,y)是有界闭区域D上的有界函数,将区域D任意分割成n个小区域

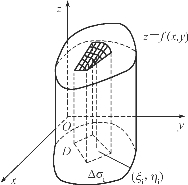
图6-20

其中,Δσi表示第i个小区域,也表示它的面积.任取一点(ξi,ηi)∈Δσi,作和式

如果当各小区域的直径的最大值λ趋于零时,极限

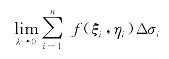
存在,则称此极限为函数z=f(x,y)在区域D上的二重积分,记作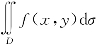,即

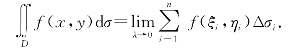
其中,f(x,y)称为被积函数,D称为积分区域,f(x,y)dσ称为被积表达式,dσ称为面积元素,x和y称为积分变量.

若函数f(x,y)在有界闭区域D上的二重积分存在,则称f(x,y)在D上可积.

注意：

(1)函数z=f(x,y)在区域D上的二重积分与区域D的分法无关,也与点(ξi,ηi)的取法无关.只与函数z=f(x,y)及积分区域D有关.

(2)二重积分中的面积元素dσ可由将D划分成小区域Δσi的图形来确定.如图6-21中,使用一组与x轴平行的直线和一组与y轴平行的直线来划分区域D,因此,Δσi是一个长宽各为Δxi,Δyi的长方形,其面积为Δσi=ΔxiΔyi.

这时,面积元素就为dxdy,即dσ=dxdy.

二重积分即可表示为：

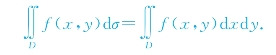
由此可见,使用不同的曲线划分区域,会得到不同的面积元素.

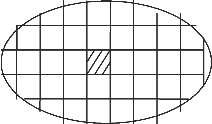
图6-21

3.二重积分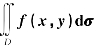的几何意义

二重积分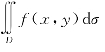的几何意义是明显的：设在区域D上f(x,y)≥0,则二重积分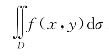表示以区域D为底,以曲面z=f(x,y)为曲顶的曲顶柱体的体积.若在区域D上f(x,y)≤0,则上述曲顶柱体在xOy面的下方.二重积分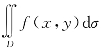的值是负的,它的绝对值为该曲顶柱体的体积.

6.6.2　二重积分的基本性质

二重积分与定积分有类似的性质.

设f(x,y),g(x,y)在有界闭区域D上均可积,则

性质1 .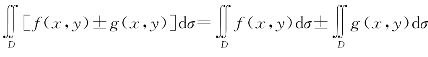

性质2 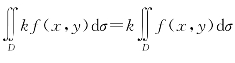(k为常数).

性质3 如果区域D被连续曲线分割为D1与D2两部分,则

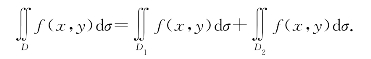
性质4 如果区域D上有f(x,y)≤g(x,y),则

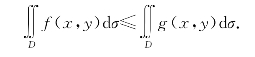
性质5 设M和m分别为函数f(x,y)在有界闭区域D上的最大值和最小值,则

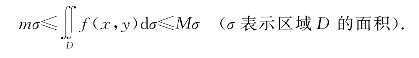
性质6 二重积分中值定理：设f(x,y)在有界闭区域D上连续,σ是区域D的面积,则在D上至少存在一点(ξ,η),使得

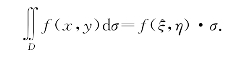
上式右端是以f(ξ,η)为高、以D为底的平顶柱体的体积.

6.6.3　二重积分的计算

在实际应用中,直接由二重积分的定义、性质来计算二重积分一般是很困难的.下面介绍一种计算二重积分的较为简单的方法,这种方法是把二重积分逐次分解为两个一重积分(定积分)进行计算.

视频82

1.直角坐标系中的二重积分计算

由二重积分的定义知道,当f(x,y)在区域D上可积时,其积分值与区域D的分割方法无关,因此在直角坐标系中,可用分别平行于x轴和y轴的直线将区域D分成许多小矩形,这时,面积元素dσ=dxdy,二重积分也可记为

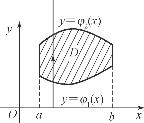
图6-22

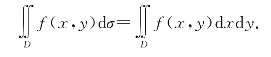
(1)设z=f(x,y)≥0,区域D可以表示为

其中,φ1(x),φ2(x)在[a,b]上连续,则称D为X-型区域(图6-22).

根据二重积分的几何意义等于以D为底,以z=f(x,y)为顶的曲顶柱面的体积(图6-23)；另一方面,用“平行截面面积为已知的立体体积”的计算方法来计算这个立体体积,先计算截面面积.

为此,用一组平行于yOz坐标平面的平面x=x0(a≤x0≤b)截该曲顶柱面,如图6-23所示,所得截面是[φ1(x0),φ2(x0)]区间上,以曲线z=f(x0,y)为曲边的曲边梯形(图6-23)的阴影部分,由定积分的几何意义可知,这个曲边梯形的面积S(x0)为

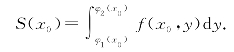
因此,过区间[a,b]中任意一点x,且平行于坐标面yOz的平面截曲顶柱体所截得的截面面积为

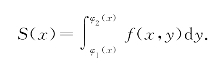
其中,在关于y的积分过程中将f(x,y)中的x视为常数.

再由截面面积为已知的立体体积的求法,便得到该曲顶柱体的体积为

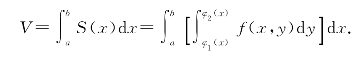
于是

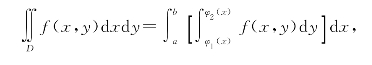
常记为

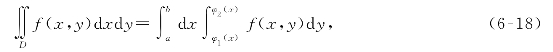
称上式为先对y,后对x的二次积分.

虽然以上的推导过程中,假设z=f(x,y)≥0,但事实上,式(6-18)的成立并不受此条件的限制.因此,无论z=f(x,y)是否大于等于零,式(6-18)总是成立的.

(2)若区域D可以表示为

其中ψ1(y),ψ2(y)在[c,d]上连续,则称D为Y-型区域(图6-24).类似可得

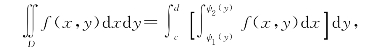
或记为

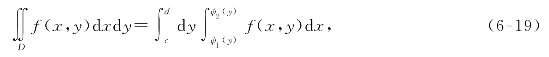
称上式为先对x,后对y的二次积分.

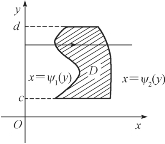
图6-24

注意

(1)由上述分析可知,在计算二重积分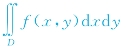的过程中,首先应当将积分区域D用不等式φ1(x)≤y≤φ2(x),a≤x≤b或ψ1(y)≤x≤ψ2(y),c≤y≤d表示出来,并画出其示意图.

特别地,若积分区域D为矩形区域：a≤x≤b,c≤y≤d,被积函数为f(x,y)=f1(x)f2(y)时,则有

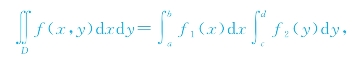
即二重积分可化为两个一元函数定积分的乘积.

(2)如果积分区域既不是X-型区域,也不是Y-型区域时,但总是可以分为若干个小块D1,D2,…,Dk,且每个小块都是X-型区域或Y-型区域,可利用二重积分的性质来计算.

例6.28 计算其中,D={(x,y)|0≤x≤1,0≤y≤2}.(www.xing528.com)

解 将区域D看作是X-型区域：0≤x≤1,0≤y≤2是矩形,故

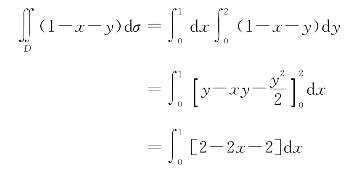
例6.29 计算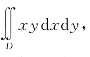其中D由直线y=x,x=1,y=0围成.

解法一 画出区域D的图形,如图6-25所示,可将区域D看作是X-型区域.即先对y积分.

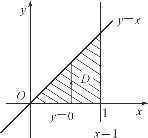
图6-25

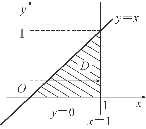
图6-26

根据图形知,D可表示为：0≤y≤x,0≤x≤1,因此

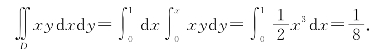
解法二 画出区域D的图形,如图6-26所示,可将区域D看作是Y-型区域,即先对x积分.

可将D表示为：y≤x≤1,0≤y≤1,因此

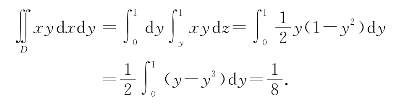
例6.30 计算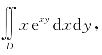其中,D是长方形区域：0≤x≤1,-1≤y≤0.

解 选择先对y积分.

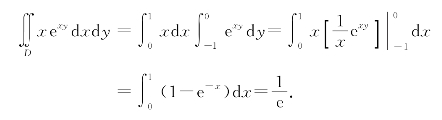
注：如果先对x积分,需要利用分部积分法,计算过程会较复杂.

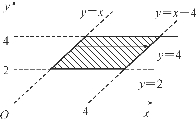
图6-27

例6.31 计算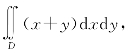其中D由直线y=2、y=4、y=x、y=x-4围成.

解 画出区域D的图形,如图6-27所示,D可表示为：y≤x≤y+4,2≤y≤4,这是一个Y-型区域(先对x积分),则

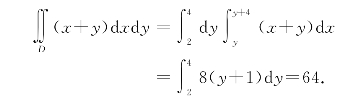
注：若先对y积分,要用平行于y轴的直线将区域D分成三个X-型区域D1,D2,D3(图6-28).分别求这三个X-型区域上的二重积分,最后利用积分可加性把它们相加即得.

由以上例题可以看出,将二重积分化为二次积分时,在选择积分次序时,不仅要考虑被积函数的特点,还要看积分区域的特征.积分次序选择得恰当,能简化积分的计算.

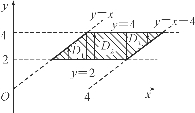
图6-28

例6.32 用两种不同次序的二次积分表示出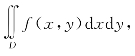其中,D由x轴(即y=0)和直线y=x,y=2-x围成.

解 画出区域D的图形(图6-29).

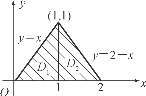
图6-29

可将区域D看作是Y-型区域(先对x求积分),

则D可表示为0≤y≤1,y≤x≤2-y.

故

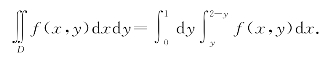
若将区域D看作是X-型区域(先对y求积分),则D表示为D1：0≤x≤1,0≤y≤x和D2：1≤x≤2,0≤y≤2-x.

故

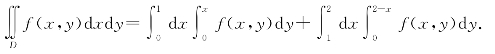
注：在求二重积分时,可通过交换积分次序来进行计算.

例6.33 通过交换积分次序计算二次积分.

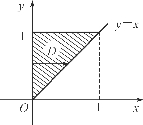
图6-30

解 由于不定积分的原函数不能用初等函数表示出来,因此,需通过交换积分次序的方法来计算这个二重积分(即变成先求关于x的积分).

由题可知,积分区域D={(x,y)|0≤x≤1,x≤y≤1},如图6-30所示；而D也可写成：D={(x,y)|0≤y≤1,0≤x≤y}.

所以

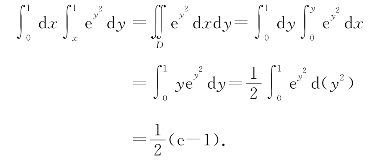
此例表明：在计算已给的二次积分时,往往需要使用交换积分次序的方法来计算.

*2.极坐标系下二重积分的计算

在前面学习二重积分的定义时,可以发现,用不同的曲线划分区域D时,面积元素dσ有不同的表示.直角坐标系下,我们用一组平行于x轴的直线和一组平行于y轴的直线划分区域D,得到面积元素dσ=dxdy.下面讨论在极坐标系下二重积分的计算问题.

在极坐标系下,用两组曲线r=常数及θ=常数(即一组同心圆与一组过原点的射线),将区域D任意分成许多小区域(图6-31).设dσ是r到r+dr和θ到θ+dθ之间的小区域,当无限细分时,可以把小区域dσ近似看作小矩形,它的边长分别为dr和rdθ,因此得极坐标系下的面积元素dσ=rdrdθ.

由直角坐标与极坐标的关系x=rcosθ,y=rsinθ得

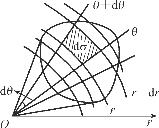
图6-31

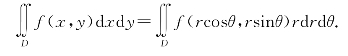
上式右端D的边界曲线要用极坐标方程表示.

同直角坐标系计算二重积分一样,极坐标系下计算二重积分也化为二次积分来计算.也就是,要将上式右端化为二次积分,而在将上式右端化为二次积分时,通常是选择先对r积分,后对θ积分的次序.积分限的确定一般有以下三种情形.

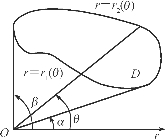
图6-32

(1)极点O在区域D的外部.

积分区域D是由极点出发的两条射线θ=α,θ=β和两条连续曲线r=r1(θ),r=r2(θ)围成(图6-32)：

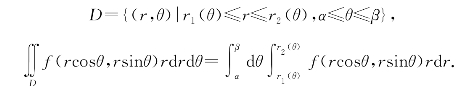
例6.34 计算,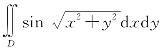

其中D为圆环：π2≤x2+y2≤4π2.

解 在极坐标系下,区域D的内环连续曲线为r=π,外环连续曲线为r=2π.极点在区域

D之外.D可以表示为

D={(r,θ)|π≤r≤2π,0≤θ≤2π}.

故

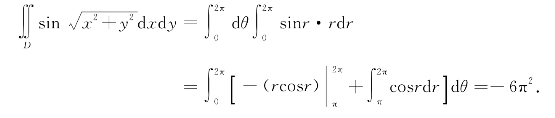
(2)极点O在区域D的边界上.

积分区域D是由极点出发的两条射线θ=α,θ=β和连续曲线r=r(θ)围成(图6-33)：

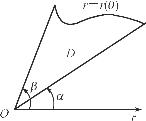
图6-33

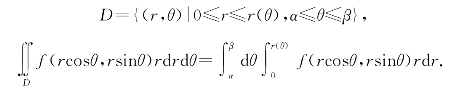
例6.35 计算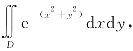其中,D为区域：x2+y2≤1,x≥0,y≥0.

解 在极坐标系下,区域D可以表示为

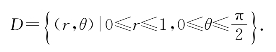
因极点在区域D的边界上,故

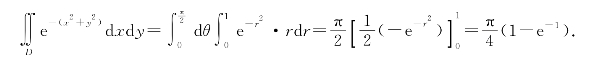
(3)极点O在区域D的内部.

积分区域D由连续曲线r=r(θ)围成,如图6-34所示.

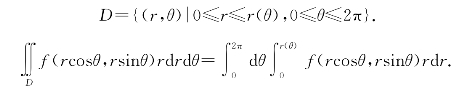
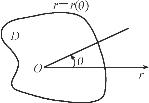
图6-34

例6.36 计算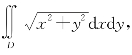其中D为圆域：x2+y2≤1.

解 利用直角坐标计算较复杂,故下面利用极坐标采计算.区域D表示为

D={(r,θ)|0≤r≤1,0≤θ≤2π}.

因极点在区域D内部,故

由上面例题知：如果积分区域D为圆域、扇形域或被积函数为f(x2+y2)时,采用极坐标计算二重积分比较方便.

习题6-6答案