多元复合函数和隐函数微分法

6.4.1　复合函数的求导法则

在一元函数微分学中,复合函数求导法则是最重要的求导法则之一,它解决了很多复杂函数的求导问题.在多元函数微分学中同样如此,下面介绍二元复合函数的求导法则.

定理6.1 设函数u=φ(x,y),v=ψ(x,y)在点(x,y)处偏导数存在,函数z=f(u,v)在对应点(u,v)处可微,则二元复合函数z=f[φ(x,y),ψ(x,y)]在点(x,y)处偏导数存在,且

对于二元复合函数的这个求偏导数的法则,我们可借助图6-14来帮助理解,更好地掌握式(6-2)和式(6-3)的应用方法.

图6-14

在求偏导数时,如将y看作常数,函数就可看作x的一元函数；由于当x改变时,既会引起u改变,同时也会引起v改变,从而引起z改变.因此,由x引起的z的变化由两部分组成.由变量关系图(图6-14)看到从函数z到自变量x有两条路径：z→u→x及z→v→x；沿z→u→x路径,对应有, 沿z→v→x路径,对应有·只要将两项相加,即得式(6-2).可用同样的方法来理解求的式(6-3).

式(6-2)和式(6-3)所表示的求导法则,也常称为复合函数的链式法则.

例6.15 已知,求.

解 令u=ex+y2,v=x2+y,则z=ln(u2+v).

由式(6-2)和式(6-3)得

例6.16 设z=f(x+y,xy),求.

解 设u=x+y,v=xy,则z=f(u,v),尽管这是个抽象函数,但各变量间的关系如图6-14所示,因而有

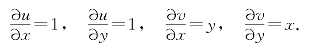
由式(6-2)、式(6-3)得

如果记表示函数z对第i个中间变量的偏导数,即可记为可记为f′2,则上面的结果可改为

此例表明：计算抽象复合函数的偏导数时,在求出的偏导数结果中,包含有抽象的偏导数的符号是常见的.

二元函数的复合形式可以是多种多样的,要善于分析函数间的复合关系.下面针对几种常见的特殊情形加以分析.

(1)已知z=f(u,v),u=φ(x),v=ψ(x),则z=f[φ(x),ψ(x)]是x的函数,其变量关系如图6-15所示,此时,z对x的导数称为全导数,且有

图6-15

例6.17 设z=uv,u=ex,v=cos2x,求全导数.

解 题中各变量z和u,v,x有如图6-15描述的关系,由式(6-4)得

(2)已知z=f(u,v,w),u=u(x,y),v=v(x,y),w=w(x,y),其变量关系如图6-16所示,则

(3)已知z=f(u),u=φ(x,y),其变量关系如图6-17所示,则

例6.18 设z=f(x2+y2),f是可微函数,求证：.

图6-16

图6-17

证明 设u=x2+y2,则z=f(x2+y2)是由z=f(u),u=x2+y2复合而成的.

图6-17描述了各变量的关系,由式(6-7)和式(6-8)得

所以有

(4)已知z=f(u,x,y),u=φ(x,y),其变量关系如图6-18所示,则

例6.19 设z=f(x,y,u)=(x+y)sinu+eu,u=x2+y2,求.

图6-18

解 图6-18描述了变量z和u,x,y的关系.由式(6-9)和式(6-10)得

(www.xing528.com)

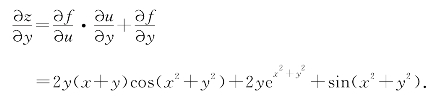
注意：式(6-9)中的和代表不同的意义是复合函数z=f[φ(x,y),x,y]把y看作常数,对x求偏导数；而是函数z=f(u,x,y)中把u,y都看作常数(虽然u与x有关),对x求偏导数.为了避免混淆,将上面式子中右端第一项写成表示函数f(u,x,y)对第二个变量x求偏导数.同理,式(6-10)中的所表示的含义与式(6-9)中的解释类似.

例6.20 设z=f(x,xcosy),求.

解 设u=xcosy,则z=f(x,u).

图6-19描述了函数中各变量的关系,所以得

图6-19

从上面例题知：在使用链导法则求偏导数时,无论因变量与中间变量、自变量之间是什么形式的关系,画出各变量(即因变量、中间变量、自变量)间的关系图至关重要.

*6.4.2 隐函数求导

1.由方程F(x，y)=0所确定的隐函数y=f(x)的导数的求法

由方程F(x,y)=0所确定的隐函数y=f(x)是一元隐函数,一元隐函数的求导方法在上册已经学习过,我们通过二元复合函数的求导法,来推导出隐函数的导数公式.

假设由方程F(x,y)=0确定了一个可导的隐函数y=f(x),将方程F(x,y)=0所确定的隐函数y=f(x)代入F(x,y)=0,得恒等式

F(x,f(x))≡0.

由于上式左端可看作是x的复合函数,因此,两边同时对x求其导数,即得

分别用表示, 即有.

若有F′y≠0,则隐函数y=f(x)的导数为

例6.21 求由方程exy+x=y所确定的隐函数的导数.

解 设F(x,y)=exy+x-y,则

代入式(6-11),得

此例表明：用式(6-11)求时,在计算F′x、F′y时,把x,y看成两个独立的变量,不能再把y看成x的函数,即求F′x时,是把y看作常数只对x求导,求时,是把x看作常数只对y求导.

2.由方程F(x，y，z)=0所确定的隐函数z=f(x，y)的导数的求法

与推导公式(6-11)类似,把z=f(x,y)代入方程F(x,y,z)=0中,得

F(x,y,f(x,y))=0.

上式左边F(x,y,f(x,y))可看作一个复合函数,对等式两边分别关于x,y求偏导,得

分别用F′x,F′y,F′z表示和.

若F′x(x,y,z)≠0,则可得

例6.22 设z2y-xz3=1,求.

解 设F(x,y,z)=z2y-xz3-1,则

由式(6-12)和式(6-13),得

例6.23 设x2+y2+z2-4z=0,求.

解 设F(x,y,z)=x2+y2+z2-4z,则

由式(6-12)得

再对x求一次偏导数,得

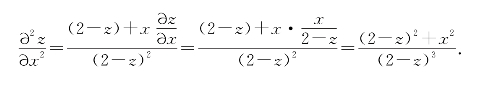
注意：用式(6-12)和式(6-13)求时,在计算F′x,F′y,F′z的过程中,要将x,y,z看成独立的变量.即在求F′x时,要把y,z当作常数,只对x求偏导数；在求F′y时,要把x,z当作常数,只对y求偏导数；在求F′z时,要把x,y当作常数,只对z求偏导数.

习题6-4答案