高等数学·下册偏导数的概念与定义

6.3.1　偏导数的概念

1.偏导数的定义

在研究一元函数时,我们已经知道导数就是函数的变化率,它反映了函数在某一点变化的快慢程度.对于二元函数同样需要研究它的变化率,然而,由于自变量多了一个,因而,二元函数与自变量的关系要比一元函数复杂得多.在xOy平面内,当点(x,y)沿不同的路径趋于点(x0,y0)时,函数f(x,y)的变化快慢一般来说是不同的.这就需要讨论函数f(x,y)在点(x0,y0)处沿各个不同方向的变化率.

本书仅研究二元函数z=f(x,y)当点(x,y)分别沿平行于x轴、y轴趋于点(x0,y0)这两种特殊的变化形式,即：如果自变量x变化,则自变量y保持不变(可看作常量)；而如果自变量y变化,则自变量x保持不变(可看作常量)下的变化率.这不仅是由于在以上两种变化方式下讨论的时候比较简单,应用广泛,而且也是研究其他方向变化率的基础.

定义6.2 设某二元函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,当固定y=y0,而x在x0处有增量Δx时,相应的函数有增量(称为函数z对x的偏增量,记为Δzx)

Δzx=f(x0+Δx,y0)-f(x0,y0).

如果极限

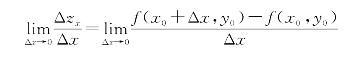
存在,则称此极限值为函数z=f(x,y)在点(x0,y0)处对x的偏导数：

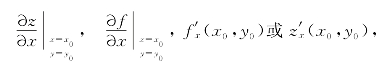
即

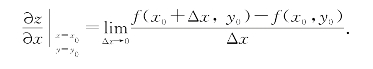
类似地,函数z=f(x,y)在点(x0,y0)处对y轴的偏导数定义为

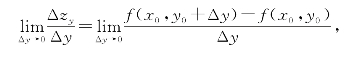
记为

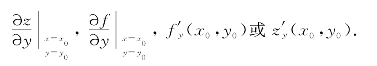
如果函数z=f(x,y)在区域D内每一点(x,y)处都存在对x的偏导数,则这个偏导数仍是x、y的函数,称此函数为z=f(x,y)对自变量x的偏导函数,记为

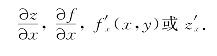
类似地,可以定义函数z=f(x,y)对自变量y的偏导数,记为

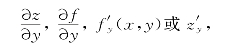
且有

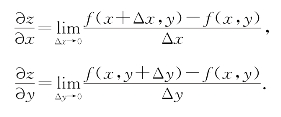
注意

(1)函数z=f(x,y)在点(x0,y0)处对x的偏导数f′x(x0,y0),就是偏导函数f′x(x,y)在点(x0,y0)处的函数值,而f′y(x0,y0)就是偏导函数f′y(x,y)在点(x0,y0)处的函数值.在不至于混淆的情况下,常把偏导函数简称为偏导数.

(2)偏导数的记号是 一个整体记号,不能理解为∂z与∂x之商,这一点与一元函数的导数记号不同可以看成函数微分dy与自变量微分dx之商.

二元以上的多元函数的偏导数可类似地定义.

2.二元函数偏导数的几何意义

由空间解析几何知识,我们知道曲面z=f(x,y)被平面y=y0截得的空间曲线为

因此,二元函数z=f(x,y)在点(x0,y0)处对x的偏导数f′x(x0,y0),就是一元函数z=f(x,y0)在点x=x0处的导数.由一元函数导数的几何意义知,二元函数z=f(x,y)在点(x0,y0)处对x的偏导数,就是平面y=y0上的一条曲线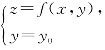在点M0(x0,y0,f(x0,y0))处的切线M0Tx对x轴的斜率.

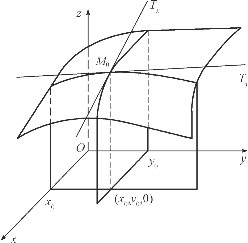
图6-13

同样,f′y(x0,y0)表示曲线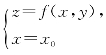在点M0处的切线M0Ty对y轴的斜率(图6-13).

3.偏导数的求法

由偏导数定义知,函数z=f(x,y)对x的偏导数就是把y看成常数,函数z=f(x,y)视为以x为自变量的一元函数,对这个一元函数求关于x的导数.同样,求z=f(x,y)对y的偏导数时,就将x看成常数,对函数z=f(x,y)关于y求导数即可.

由此可见,计算二元函数的偏导数就归结为计算一元函数的导数,因此,一元函数的求导公式、求导法则均可以在求偏导数过程中运用.

例6.11 设z=2x2y5+y2+2x,求.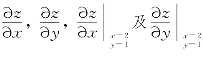

解 要求即把y看成常数,函数看成是以x为自变量的一元函数,然后对x求导数,得

(www.xing528.com)

同理可得

所以

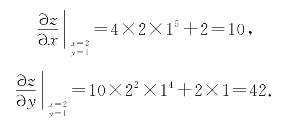
例6.12 求下列函数的偏导数：

(1)z=(2)z=xy,(x＞0,x≠1)；(3)z=sin(x2y).

解 (1)利用一元复合函数的求导法则,有

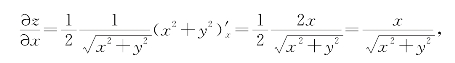
由对称性可知

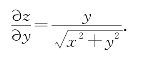
(2)把y看成常数,z=xy为关于x的指数函数,则

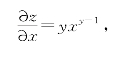
把x看成常数,z=xy为关于y的指数函数,则

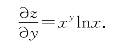
(3)由一元复合函数的求导法则得

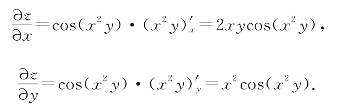
6.3.2　高阶偏导数

定义6.3 设函数z=f(x,y)在区域D内的每一点(x,y)都有偏导数

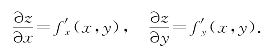
如果偏导函数f′x(x,y),f′y(x,y)分别对x、y的偏导数仍存在,则称这些偏导数是函数z=f(x,y)的二阶偏导数.由求偏导数的顺序不同,二阶偏导数有下列四种类型：

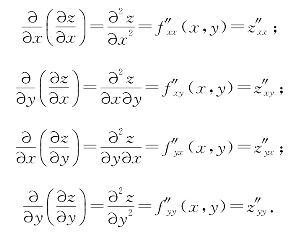
上面第二、第三两个二阶偏导数称为函数z=f(x,y)的二阶混合偏导数,它们分别都是对x,y各求一次导数,但不同的是求导的次序不一样.第二个二阶偏导数,即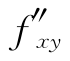(x,y),是先对x、后对y求偏导数；而第三个二阶偏导数,即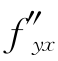(x,y),是先对y、后对x求偏导数.

用同样的方法,可以得到三阶、四阶以至n阶偏导数(如果存在的话).二阶或二阶以上的偏导数统称为高阶偏导数.

例6.13 设z=x2y+sin(xy),求它的二阶偏导数.

解 因为

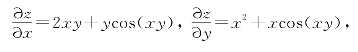
所以

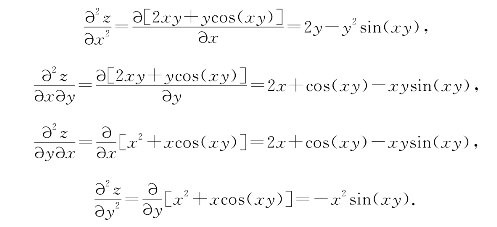
注意：从上例可以看到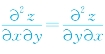(即两个混合偏导数是相等的),需要注意的是,这样的结论并不是在任何时候都成立.只有当两个二阶混合偏导数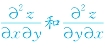在求导区域D内连续时,则在该区域内有

也就是说,当两个二阶混合偏导数在求导区域内连续时,我们求二阶混合偏导数与求导的次序无关.这个结论也可以类推到更高阶的混合偏导数.

例6.14 设f(x,y)=exy+sin(x+y),求.

解 因为

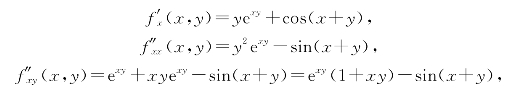
所以

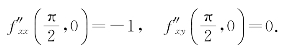
习题6-3答案