高数下册：二元函数及多元函数

6.2.1　二元函数的定义

在实际问题中所涉及的函数,并非都是一元函数,常常会遇到一个变量依赖于两个或更多个自变量的情形,如：

例6.6 矩形面积S与其长x、宽y有下列依赖关系：

S=xy (x＞0,y＞0),

其中,长x与宽y是独立取值的两个变量.在它们的变化范围内,当x、y取定值后,矩形面积S有唯一确定的值与之对应.

例6.7 物体的动能E与物体的质量m和运动速度v之间有如下关系：

上式中,对m,v的变化范围内的每一组值,变量E有唯一确定的值与之对应.

上述两例,去掉变量的具体意义,可得出共性,即：一个变量是由其他两个变量的变化来确定的函数,这样的函数就是二元函数.

定义6.1 设D是xOy平面上的一个点集,x、y是相互独立的两个变量,如果点(x,y)∈D,而第三个变量z按照某一对应关系f有唯一确定的数值与之对应,则称z为x,y在D上的二元函数,记作

z=f(x,y).

其中x、y称为自变量,z称为因变量,点集D称为函数的定义域,数集

视频77

{z|z=f(x,y),(x,y)∈D}

称为函数的值域.

同一元函数一样,二元函数的定义域也是确定一个二元函数的要素之一.我们知道,一元函数的定义域一般是一个区间或几个区间的并.

从二元函数的定义域概念可知,二元函数的定义域D通常是由平面xOy内一条或几条光滑曲线围成的部分平面,这样的部分平面称为区域.围成区域的曲线称为区域的边界,边界上的点称为边界点.包括边界的区域称为闭区域,不包括边界的区域的称为开区域.

分析函数变化离不开求函数的定义域.如何求二元函数的定义域?先看下面的例题.

例6.8 求函数z=ln(x+y)的定义域.

解 要使函数表达式有意义,必须有

x+y＞0,

图6-7

故函数的定义域是图6-7阴影部分所示的区域,即为D={(x,y)|x+y＞0}.

例6.9 求函数的定义域,并计算f(0,2)和f(1,-1).

解 要使函数表达式有意义,必须有

x2+y2≤4,

所以,函数的定义域是图6-8中阴影部分所示的区域,它是xOy平面上以原点为圆心,半径为2的圆内及其边界上点的全体,即为

图6-8(www.xing528.com)

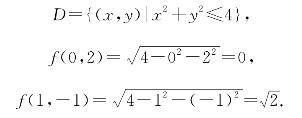
例6.10 求函数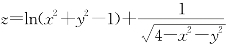的定义域.

解 要使函数有意义,x、y应满足不等式组

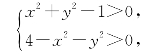
即

1＜x2+y2＜4.

因此,函数的定义域为图6-9中阴影部分所示的区域,它的图形是圆环,即为

D={(x,y)|1＜x2+y2＜4}.

从以上例题可知,求函数解析式z=f(x,y)的定义域,就是求其能使函数表达式有意义的点(x,y)的全体,一般可用不等式或不等式组表示.而求对于从实际问题提出的函数的定义域时,还要根据自变量所表示的实际意义来确定.

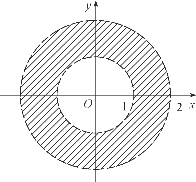
图6-9

从上面的例子还可以看到二元函数的定义域可以用平面内各种形式的图形来描绘.

为便于问题的分析,我们把以点P0(x0,y0)为圆心、以δ＞0为半径的开区域即满足不等式的点的全体称为点P0的δ邻域,记为U(P0,δ)(图6-10).若在P0的δ邻域中去掉点P0,则称此区域为点P0的去心δ邻域,记为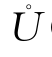(P0,δ),也记为(P0).

若区域D可以被包含在某个圆内,则称D是有界区域(图6-8),否则称为无界区域(图6-7).

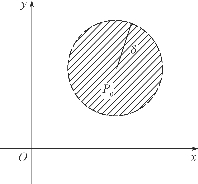
图6-10

6.2.2　二元函数的几何意义

一般地,一元函数y=f(x)的图形在xOy平面上表示一条曲线.

对于二元函数z=f(x,y),设其定义域为D,P0(x0,y0)为函数定义域中的一点,与点P0对应的函数值记为z0=f(x0,y0),于是可在空间直角坐标系O-xyz中作出点M0(x0,y0,z0).当点P(x,y)在定义域D内变动时,对应点M(x,y,z)的轨迹就是函数z=f(x,y)的几何图形.

一般来说,它通常是一张曲面.这就是二元函数的几何意义,而定义域D正是这曲面在xOy平面上的投影,如图6-11所示.

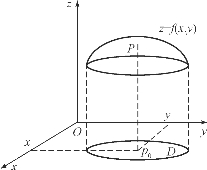
图6-11

图6-12

例如：二元函数表示以点(0,0,0)为球心、以2为半径的位于xOy平面上方的半球面(图6-12).

而函数的定义域为x2+y2≤22,即为以坐标原点为圆心、以2为半径的圆的内部及其边界(图6-8).

6.2.3　多元函数的定义

类似二元函数定义,可以定义三元函数u=f(x,y,z)以及三元以上的函数.二元及二元以上的函数统称为多元函数.

习题6-2答案