连分数的基本性质-初等数论基础

本节给出连分数的概念，并罗列连分数的一些重要性质.设n是正整数，a1，a2，…，an是一个实数列，ai＞0，i=2，3，…，n.称表达式

为有限连分数，记其为＜a1，a2，…，an＞，而称＜a1，a2，…，ak＞为该连分数的第k个渐近分数，k=1，2，…，n.特别的，当诸ai为整数时，称＜a1，a2，…，an＞为有限简单连分数.易见，有限连分数是实数，而有限简单连分数是有理数.

设a1，a2，…是一个无穷实数列且当i≥2时有ai＞0.称表达式

为无限连分数，记其为＜a1，a2，…＞，对任意正整数k，称＜a1，a2，…，ak＞为该连分数的第k个渐近分数，当诸ai为整数时，称＜a1，a2，…＞为无限简单连分数.若数列极限

存在，则称连分数＜a1，a2，…＞收敛，并称θ为该连分数的值.若上述极限不存在，则称连分数＜a1，a2，…＞发散.

下面的定理揭示了简单连分数和实数的密切关系.

定理8.1.1　关于简单连分数，有以下事实：

（1）任一有限简单连分数均为有理数.

（2）任意有理数均可表示为有限简单连分数.进一步的，非整数的有理数α有且仅有以下两种表示方式

α=＜a1，a2，…，as-1，as＞=＜a1，a2，…，as-1，1＞，s≥2，as＞1.

（3）任一无限简单连分数均收敛且其值为无理数.

（4）任意无理数均可唯一的表示为无限简单连分数.

例8.1.2　将表示为有限简单连分数.

解　作辗转相除法

62=2·23+16，23=1·16+7，16=2·7+2，7=3·2+1.

于是

于是解毕.

例8.1.3　将表示为无限简单连分数.(www.xing528.com)

解　首先计算

注意到α3=α1，有a4=a2，a5=a3…等等.故=＜2，2，4，2，4，…＞.解毕.

注8.1.4　例8.1.2和8.1.3的方法具有一般性，利用这些方法可将任意实数化为简单连分数.

以下讨论连分数的渐进分数及其在求实数的有理近似值方面的应用.

定理8.1.5　设α=＜a1，a2，…＞是无限简单连分数.记

p1=a1，p2=a1a2+1，pk=akpk-1+pk-2；

q1=1，q2=a2，qk=akqk-1+qk-2（k≥3）.

（1），k=1，2，…且

（2）对任意正整数k，有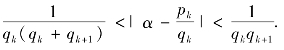　

注8.1.6　定理8.1.5对有限简单连分数也是正确的（此时k仅取有限个整数）.另外，它对一般（有限）连分数同样也是正确的.

例8.1.7　求α=的分母最小的渐近分数使其误差小于等于10-6.

解　由例8.1.3知=＜2，2，4，2，4，…＞.于是

a1=2=a2=a4=a6=a8，a3=4=a5=a7.

计算pk，qk，k=1，2，…，8如下：

由于

故所求渐近分数为解毕.