证毕：勒让德符号及初等数论基础

上节获得了判定一个正整数是否为一奇素数的二次剩余的方法.但是，当素数较大时，这个方法的计算是冗长而乏味的.为了克服这一缺点，本节引入勒让德符号并讨论它的一些重要性质.利用勒让德符号，就能很好地解决判定一个正整数是否为一奇素数的二次剩余这一重要问题.

定义6.3.1　设p是奇素数，a∈Z，定义a对p的勒让德符号如下：

定理6.3.2　设p是奇素数，a，b∈Z.

证明　　　（1）由定理6.2.5和勒让德符号的定义立得.

（2）由a≡b（modp）知

p|a⇔p|b；x2≡a（modp）有解⇔x2≡b（modp）有解.

故结论成立.

（3）在条款（1）中分别取a=1和a=-1，则

注意到　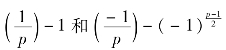的值只可能是±1，0，±2及p是奇素数，条款（3）成立.

（4）由条款（1）知

注意到的值只可能是±1，0，±2及p是奇素数，条款（4）成立.

（5）由条款（4）立得.证毕.

为探讨勒让德符号的进一步性质，需要以下重要引理.

引理6.3.3（高斯引理）　设p是奇素数，a是正整数，（a，p）=1.又设

若诸rk中大于的个数为t，则且

证明　首先，由（a，p）=1及诸k均小于p知诸rk均大于0.设是诸rk中小于的数是诸rk中大于的数.则

我们断言若不然，则但从而由（a，p）=1知p|iv+ju.由于从而2≤iv+ju≤p-1.这与p|iv+ju矛盾.注意到有

另外，对任意im，jn，有和

由（6.3.1），

注意到p与！互素，有由定理6.3.2（1）知

但　的值只能取±1，而p是奇素数，故　记

则诸rk之和即为α+β.由等式（6.3.1）知

据（6.3.2）和（6.3.3）知

但p是奇素数，故(www.xing528.com)

推论6.3.4　设p是奇素数.则　

证明　在引理6.3.3中取a=2，则

据引理6.3.3知这表明与t有相同的奇偶性，再次利用引理6.3.3便知　证毕.

推论6.3.5　设p，q是互异的奇素数.则

证明　在引理6.3.3中取a=q.则

由q是奇素数知q-1是偶数.故这表明

对偶可证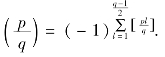证毕.

下面给出著名的二次互反定律.这个定律是1783年由欧拉首先发现的.1796年，高斯给出了它的第一个严格证明.

定理6.3.6　　　（高斯二次互反定律）设p，q是互异的奇素数.则

证明　据推论6.3.5，只需证明

在直角坐标系中以

为顶点作矩形.则此矩形的由点（0，0），确定的对角线（不包括端点）上无整点（所谓整点就是两坐标均为整数的点）.事实上，若对角线上有整点（x，y）≠（0，0），则qx-py=0.但（p，q）=1，故p|x，q|y.这导致点（x，y）在矩形之外，矛盾.容易验证，该对角线下方的三角形和对角线上方的三角形（不包括边界）中的整点数分别为

但此矩形内（不包括边界）的整点数为故（6.3.4）成立.证毕.

例6.3.7　已知383是素数.求勒让德符号的值.

解　据勒让德符号的计算性质，有

例6.3.8　已知1847是素数.判断同余方程x2≡365（mod1847）是否有解.

解　据勒让德符号的计算性质，有

据勒让德符号的定义知方程有解.解毕.

例6.3.9　求以5为二次剩余的全体奇素数.

解　设p是奇素数.则5是模p的二次剩余当且仅当由二次互反定律知

故5是模p的二次剩余当且仅当易证，当且仅当p≡1，4（mod5）时，此时p是5m±1型奇素数.换句话说，p是10n±1型素数.解毕.

例6.3.10　证明4n+1型素数有无穷多个.

证明　设p1，p2，…，pr是全体4n+1型素数.记a=（2p1p2…pr）2+1.据算术基本定理，a有奇素因数p.于是a≡0（modp），即（2p1p2…pr）2≡-1（modp）.这表明-1是模p的二次剩余.故从而p是4n+1型素数，即p是p1，p2，…，pr中之一.由p|a可知p|1，矛盾.证毕.