孙子定理：解决一次同余方程组求解问题

本节介绍著名的孙子定理，它主要解决如下形式的一次同余方程组的求解问题

其中m1，m2，…，mk是k个两两互素的正整数.

定理5.3.1（孙子定理）　设m1，m2，…，mk是k个两两互素的正整数，记

则同余方程组（5.3.1）对模m的唯一解是

其中是满足≡1（modmi）的某个整数，i=1，2，…，k.

证明　先说明满足≡1（modmi）的整数是存在的，i=1，2，…，k.事实上，由（mi，mj）=1（i≠j）知（Mi，mi）=1.据定理5.2.1知一次同余方程Mix≡1（modmi）有解.这就说明了诸的存在性.

注意到mj|Mi（i≠j），有≡0（modmj）（i≠j）.故由≡1（modmj）知

故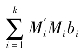满足（5.3.1）中的全部同余方程.设整数a满足（5.3.1）中的全部同余方程.则

由（mi，mj）=1（i≠j）知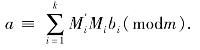证毕.

例5.3.2　解同余方程组

x≡2（mod3），x≡3（mod5），x≡2（mod7）.

解　记m1=3，m2=5，m3=7.则m1，m2，m3两两互素.再记

容易看出，

（-1）M1≡1（modm1），1·M2≡1（modm2），1·M3≡1（modm3）.

于是可取由孙子定理，该方程的解为

x≡-35·2+21·3+15·2（mod105）.

即x≡23（mod105）.解毕.

注5.3.3　例5.3.2实际上就是《孙子算经》里记载的“物不知数问题”.它的原始说法是“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？”“答曰二十三”.《孙子算经》提出了解一次同余方程组的问题并给出了较为完满的回答，这也是定理5.3.1称为孙子定理的原因.在国外，定理5.3.1及其若干推广形式统称为“中国剩余定理”（Chinese Remainder Theorem）.

由孙子定理成立的条件可以看出，孙子定理处理的一次同余方程组必须满足两个条件：各一次同余方程的“一次项系数”为1；各一次同余方程的模两两互素.这表明并非所有一次同余方程组都可用孙子定理求解.但下面的例子指出，一些不能直接用孙子定理求解的同余方程组，通过某种转化后就可用孙子定理求解.下述两个例题在一定程度上展示了一般的一次同余方程组的求解方法和思路.先介绍一个技术性结果.

命题5.3.4　设m1，m2是正整数，a∈Z，（m1，m2）=1.则对任意整数x，有x≡a（modm1m2）当且仅当x≡a（modm1）且x≡a（modm2）.

证明　这是命题4.1.3和命题4.1.4（4）的直接推论.证毕.

例5.3.5　解同余方程组

x≡3（mod8），x≡11（mod20），x≡1（mod15）.

解　据命题5.3.4知

x≡11（mod20）⇔x≡11（mod4），x≡11（mod5）

⇔x≡3（mod4），x≡1（mod5）.(www.xing528.com)

类似可知x≡1（mod15）当且仅当x≡1（mod3），x≡1（mod5）.于是，原同余方程组与同余方程组x≡3（mod8），x≡1（mod5），x≡1（mod3）等价.由孙子定理可解得原同余方程组的解为x≡91（mod120）.解毕.

例5.3.6　解同余方程组4x≡6（mod14），9x≡15（mod33）.

解　先分别解同余方程4x≡6（mod14）和9x≡15（mod33），它们的解分别为

x≡5，12（mod14）和x≡9，20，31（mod33）.

故原同余方程组的解为

x≡5（mod14），x≡9（mod33）或x≡5（mod14），x≡20（mod33）或

x≡5（mod14），x≡31（mod33）或x≡12（mod14），x≡9（mod33）或

x≡12（mod14），x≡20（mod33）或x≡12（mod14），x≡31（mod33）.

由孙子定理可知

x≡75，383，229，306，152，460（mod462）

就是原方程组的所有解.解毕.

本节的最后，通过例子来了解一下孙子定理在解同余方程方面的运用.

例5.3.7　解同余方程19x≡556（mod1155）.

解　注意到1155=3×5×7×11及3，5，7，11两两互素，据命题5.3.4知19x≡556（mod1155）当且仅当

19x≡556（mod3），19x≡556（mod5），19x≡556（mod7），19x≡556（mod11）

当且仅当

x≡1（mod3），x≡-1（mod5），x≡2（mod7），x≡-2（mod11）.

这样，利用孙子定理就可求出该同余方程的解x≡394（mod1155）.解毕.

例5.3.8　解同余方程4x2+27x-12≡0（mod15）.

解　注意到15=3×5及（3，5）=1，据命题5.3.4知4x2+27x-12≡0（mod15）当且仅当

4x2+27x-12≡0（mod3），4x2+27x-12≡0（mod5）

当且仅当x2≡0（mod3），-x2+2x-2≡0（mod5）.将模3的完全剩余系-1，0，1带入x2≡0（mod3）检验可知x2≡0（mod3）有一个解x≡0（mod3）.将模5的完全剩余系-2，-1，0，1，2带入-x2+2x-2≡0（mod5）检验可知它有两个解x≡-1（mod5）和x≡-2（mod5）.故同余方程4x2+27x-12≡0（mod15）的解为

x≡0（mod3），x≡-1（mod5）或x≡0（mod3），x≡-2（mod5）.

利用孙子定理可得4x2+27x-12≡0（mod15）的2个解为x≡9，3（mod15）.解毕.